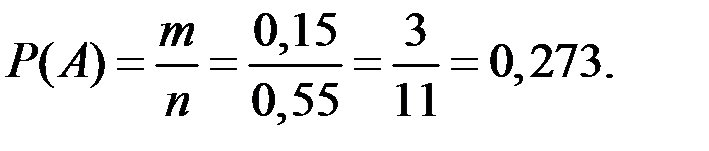Наивероятнейшее число наступлений события А в серии из n опытов удовлетворяет неравенствам
.
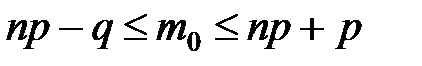3десь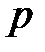 
– вероятность наступления события А в одном опыте.
Число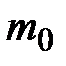 
называется наивероятнейшим числом наступления события А в n испытаниях, если 
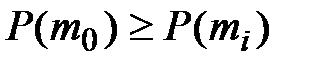при 
.
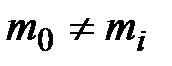Если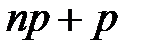 
не является целым числом, то двойное неравенство определяет лишь одно наивероятнейшее значение 
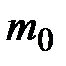. Если же 
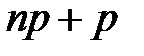целое число, то имеются два наивероятнейших значения: 
.
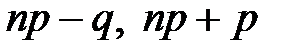Отношение числа опытов, в которых появилось событие А, к общему числу произведённых опытов, называется частотой события А или его статистической вероятностью
.
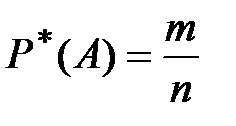Теорема Бернулли утверждает, что при неограниченном увеличении числа опытов n частота события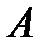 
сходится к его вероятности: 
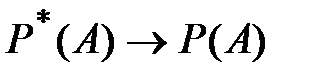, т.е. справедливо неравенство
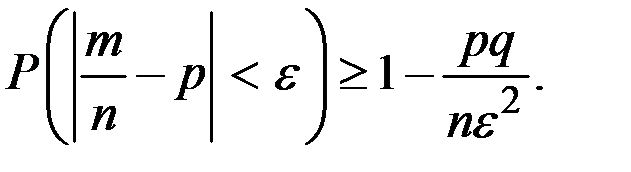
Ниже приведены примеры решения типовых прикладных задач.
Пример 1.19. Производится три независимых выстрела с вероятностью попадания 0,4 в каждом. Найти вероятность того, что будет хотя бы 2 попадания.
Решение. Искомая вероятность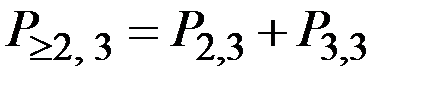 
.
Воспользуемся формулой Бернулли:
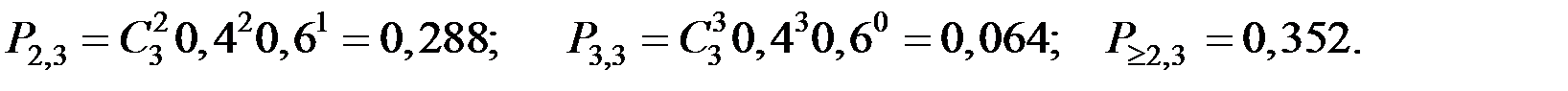
Пример 1.20. Производится 4 независимых выстрела по одной цели с различных расстояний. Вероятности попаданий в этих выстрелах равны соответственно: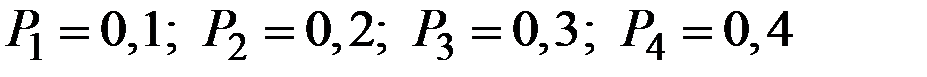 
. Найти вероятность того, что: не будет попаданий; будет ровно 3 попадания, хотя бы два.
Решение. Составляем производящую функцию
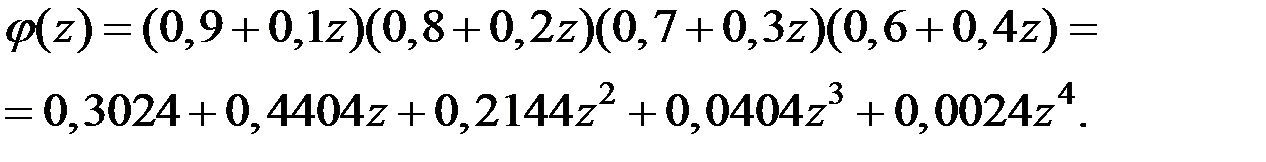
Тогда искомые вероятности:
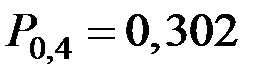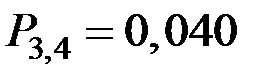4, 
4,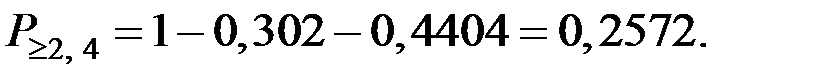 
Пример 1.21. Вероятность попадания стрелком в цель равна 0,7. Сделано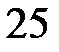 
выстрелов. Определить наивероятнейшее число попаданий.
Решение. Здесь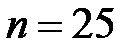 
, 
, 
.
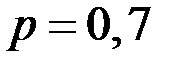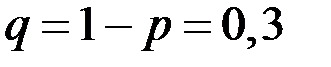Следовательно:
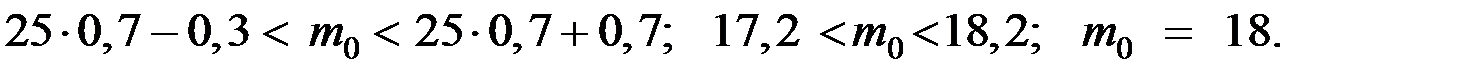
Пример 1.22. Два стрелка поочерёдно стреляют по мишени до первого попадания. Вероятность попадания первого стрелка равна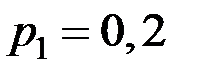 
, а второго – 
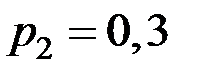. Найти вероятность того, что выиграет (попадёт) первый стрелок.
Решение. Первый стрелок выигрывает соревнование (попадает) при первом выстреле с вероятностью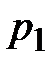 
, при втором выстреле – 
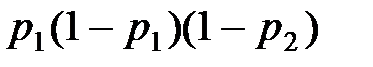(то есть здесь по одному промаху у первого и второго стрелка), при третьем выстреле – с вероятностью 
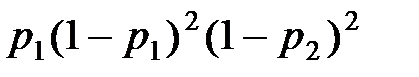(по два промаха у каждого), при n–м выстреле – с вероятностью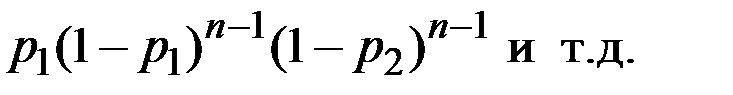 
Так как положительным исходом для первого игрока является любой из выше перечисленных исходов, то искомая вероятность будет равна сумме частных вероятностей
.
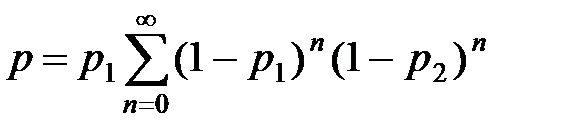С использованием формулы суммы бесконечно убывающей геометрической прогрессии получаем
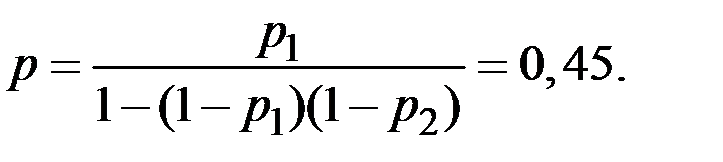
Пример 1.23. Из партии объёмом в N = 999 изделий выбираются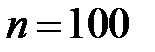 
изделий. Среди них оказалось 
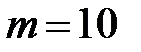дефектных. Какова наиболее правдоподобная оценка количества дефектных изделий в партии.
Решение. Наивероятнейшее число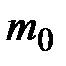 
наступлений события А в серии из n (n = 100) опытов удовлетворяет неравенствам
.
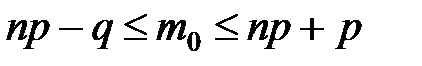3десь 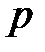– вероятность наступления события А в одном опыте:
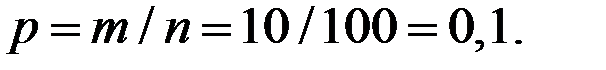
Имеем: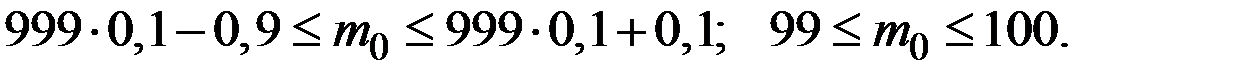 
Получили два наиболее правдоподобных значения дефектных изделий в партии: 99 и 100.
1.6. Решение типовых задач главы 1
Пример 1.24. Три предприятия могут обратиться за кредитами в три банка. Каждое предприятие выбирает себе банк случайным образом и независимо от других. Клиент, обратившийся в банк, получает кредит с вероятностью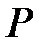 
. Найти вероятность того, что ровно в двух банках из трёх кредит будет выдан.
Решение. Пусть событие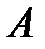 
означает, что ровно в двух банках из трёх выдан кредит. Имеем гипотезы:
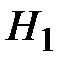– все три банка имели посетителей;
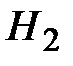– все предприятия обратились в один банк;
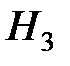– предприятия обратились к двум банкам, а третий остался не востребованным.
Тогда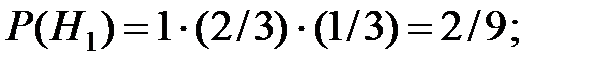 
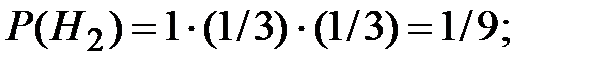
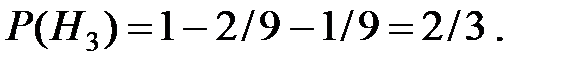
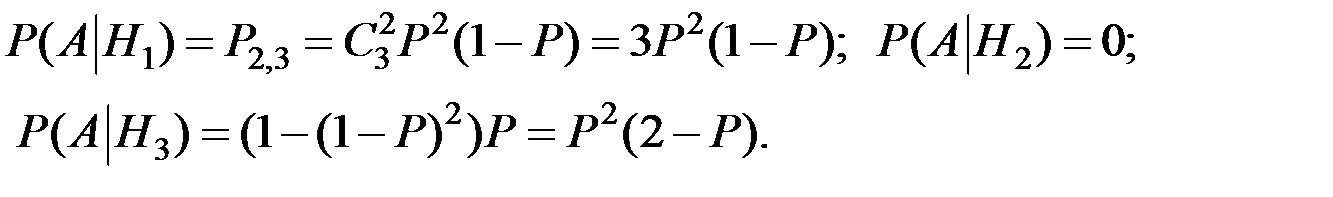
По формуле полной вероятности получаем:
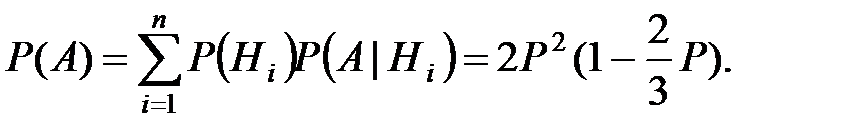
Пример 1.25. Устройство состоит из трёх независимо работающих элементов. Отказ любого элемента приводит к отказу всего устройства. Надёжность каждого элемента равна Р. Купили ещё три аналогичных элемента. Что лучше: продублировать каждый элемент или всю схему устройства в целом?
Решение. Варианты дублирования представлены на рис. 1.3.
1) 2)
Рис. 1.3. Варианты дублирования элементов устройства
Применяя формулы сложения и умножения вероятностей рассчитаем надёжность этих схем.
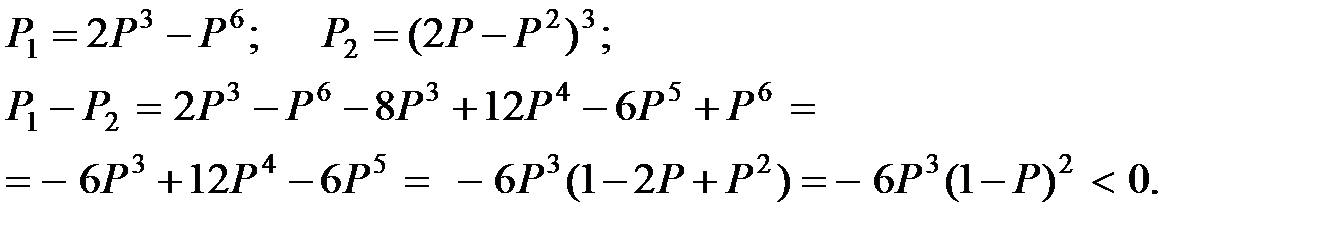
Надёжнее вторая схема.
Пример 1.26. Числа натурального ряда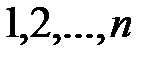 
перемешаны и расположены в случайном порядке. Какова вероятность 
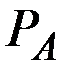того, что хотя бы одно число окажется на своём месте (т.е. будет равно номеру своего места)? Найти предел этой вероятности при возрастании n.
Решение. Пусть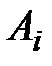 
– событие, состоящее в том, что 
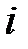–е число оказалось на своём месте.
Тогда с использованием формулы вероятности суммы событий
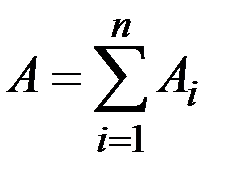
получим
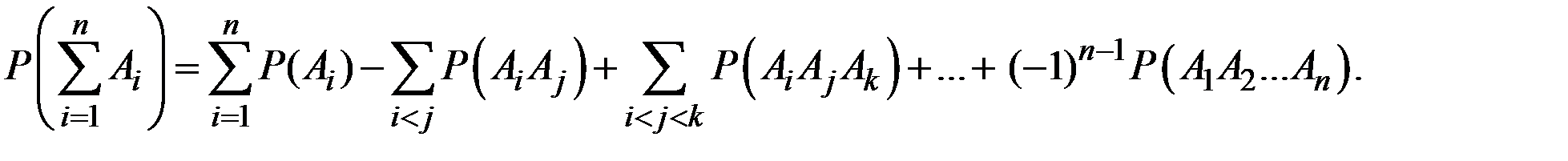
Из условия задачи можно заключить, что
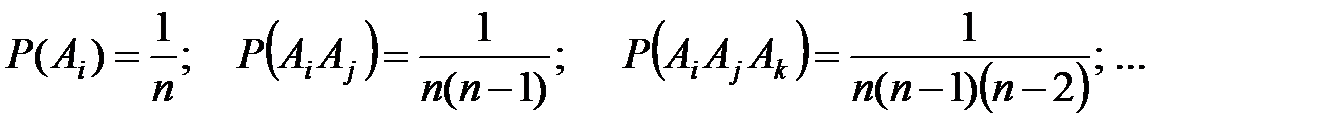
Тогда
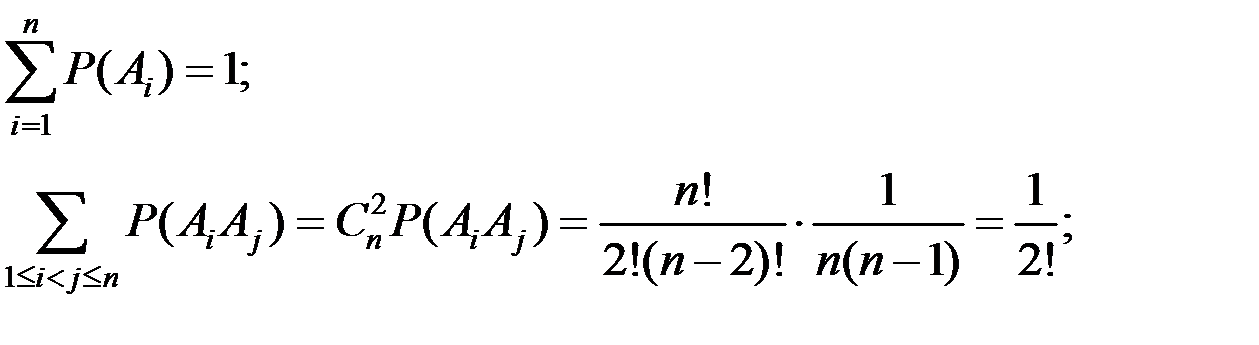
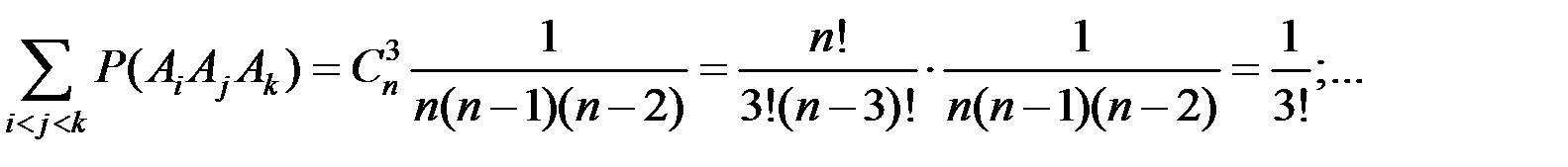
Окончательно получаем
.
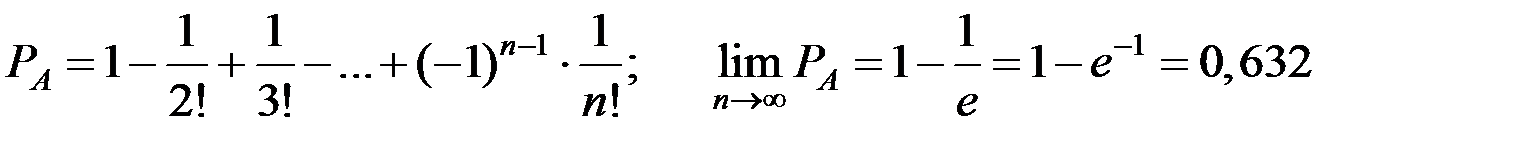Если решить эту задачу с использованием формулы Бернулли, то получим:
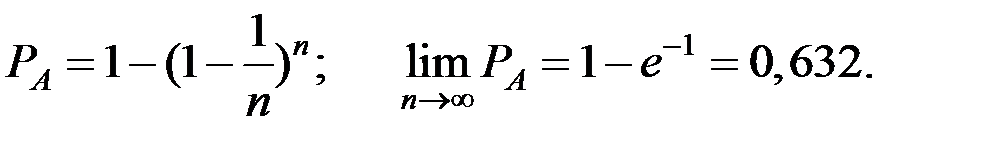
Пример 1.27. Какова вероятность купить “счастливый” билет, y которого сумма первых двух цифр номера равна сумме последних двух?
Решение. Число благоприятствующих элементарных событий m равно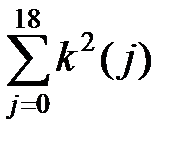 
, где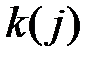 
– количество двузначных чисел с суммой цифр, равной 
, при данной сумме цифр, равной 
.
Как первую, так и вторую половину “счастливого” номера можно выбрать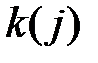 
способами, а всего способов будет 
.
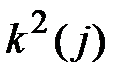Можно подсчитать, что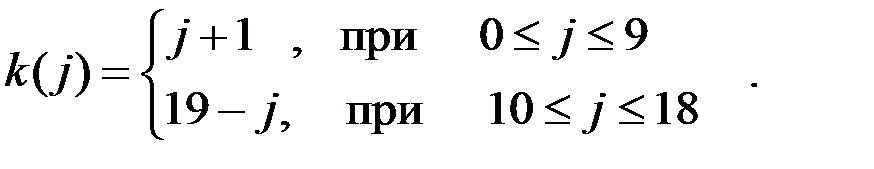 
Тогда
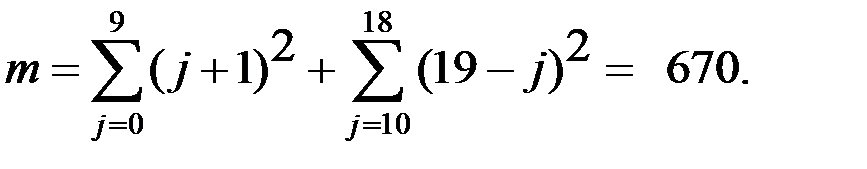
Следовательно, искомая вероятность (при n = 10000):
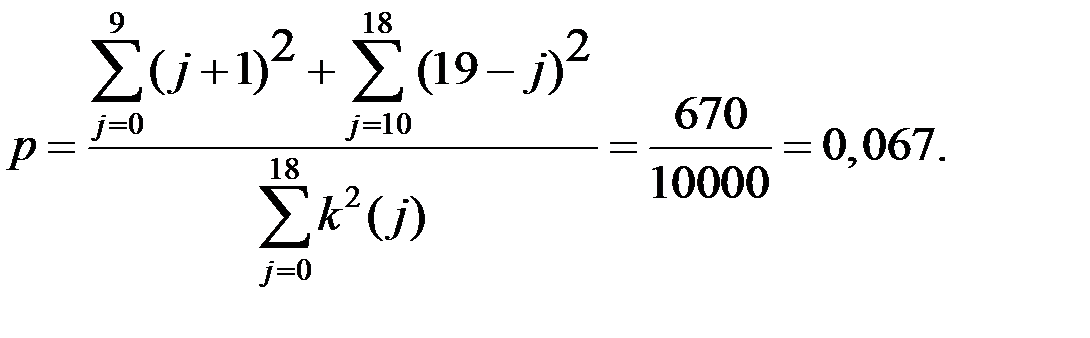
Пример 1.28. Из последовательности натуральных чисел 1, 2, ..., N отобраны n чисел х1 < х2 <...< хn . Найти вероятность того, что хm = M.
Решение.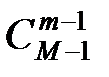 
способами можно взять числа х1, x2, ..., xm–1 и 
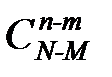способами – остальные xi.
Поэтому искомая вероятность
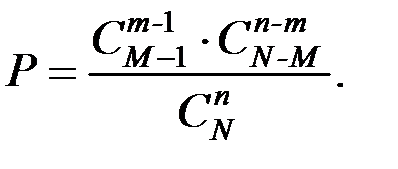
Пример 1.29. На склад поступила партия из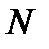 
изделий, среди которых 
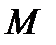дефектных. Для контроля взяли 
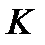изделий. Если среди контрольных окажется более 
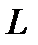бракованных, то вся партия бракуется. Какова вероятность забраковки всей партии?
Решение.
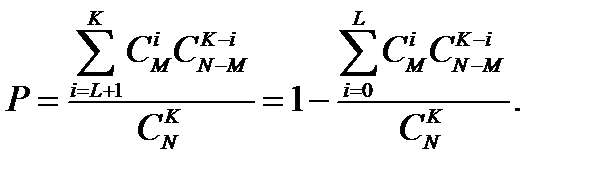
Пример 1.30. В первом ящике находится N1 деталей первого сорта и N2 деталей второго сорта, во втором ящике, соответственно, M1 и M2. Из первого ящика во второй переложено К деталей. Затем из второго ящика взяли одну деталь. Определить вероятность того, что она первого сорта.
Решение. Имеем две гипотезы:
H1 – взятая деталь принадлежит к группе из К деталей, переложенных из первого ящика во второй;
H2 – взятая деталь первоначально находилась во втором ящике.
Тогда Р(H1) =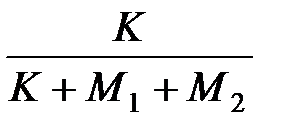 
; P(H2) = 
.
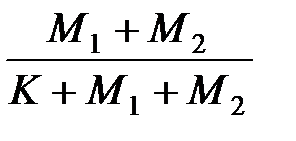Обозначим через А – событие, состоящее в том, что взятая деталь окажется первого сорта. С учётом гипотез, вероятность этого события может быть определена по формуле полной вероятности:
.
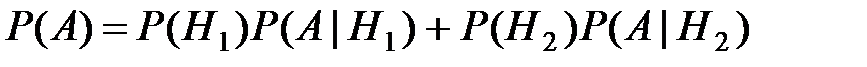Условные вероятности взятия детали первого сорта при соответствующих гипотезах будут равны:
.
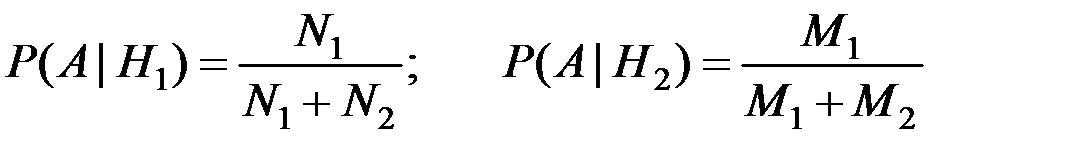Искомая вероятность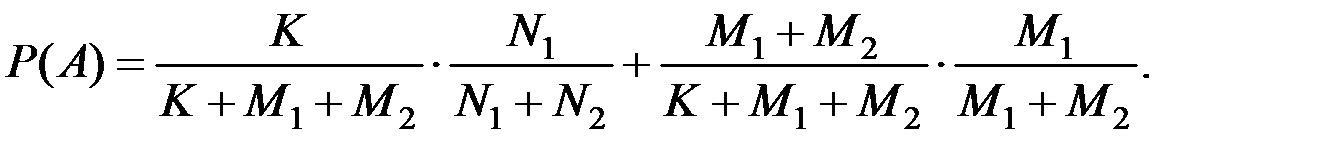 
Пример 1.31. Имеется две партии деталей, причём известно, что в одной партии все детали удовлетворяют техническим требованиям, а 25% деталей другой партии – брак. Деталь, взятая из наудачу выбранной партии, оказалась доброкачественной. Определить вероятность того, что деталь взята из второй партии.
Решение. Обозначим: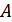 
– событие, взятая деталь доброкачественная.
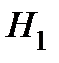– гипотеза: деталь взята из первой партии.
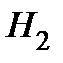– гипотеза: деталь взята из второй партии.
Имеем в силу случайности: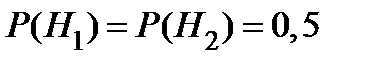 
.
Вероятность события А найдём по формуле полной вероятности:
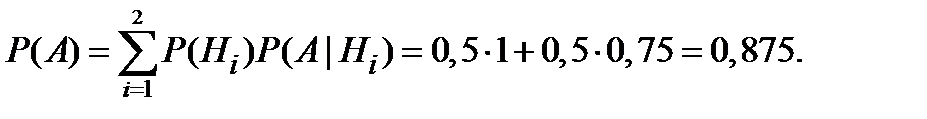
С учётом свершения события А уточним вероятность гипотезы 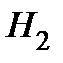по формуле Байеса:
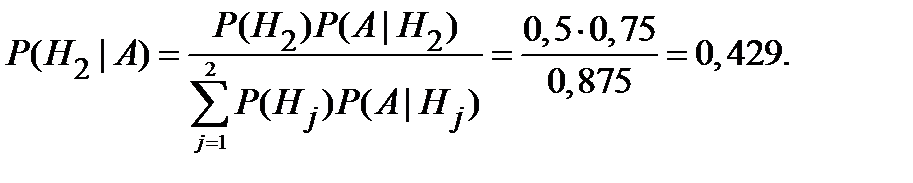
Пример 1.32. Два баскетболиста делают по 3 броска в корзину. Вероятность попадания у первого равна 0,8, у второго – 0,7. Найти вероятность того, что второй игрок будет иметь больше попаданий.
Решение. Составим таблицу распределения вероятностей с использованием формулы Бернулли:
| Число попаданий | 0 | 1 | 2 | 3 |
| Первый игрок | 0,008 | 0,096 | 0,384 | 0,512 |
| Второй игрок | 0,027 | 0,189 | 0,441 | 0,343 |
Тогда искомая вероятность:
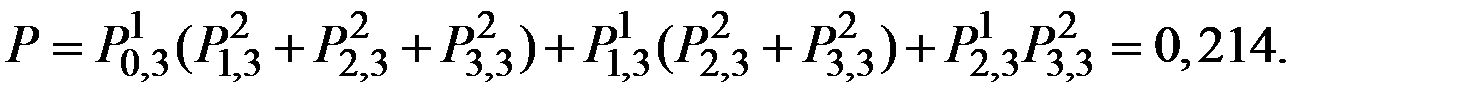
Пример 1.33. На отрезке длины L наудачу выбираются 2 точки M1 и M2. Определить вероятность того, что из полученных отрезков можно построить треугольник.
Решение. Пусть длины образованных отрезков равны x, y, L – x – y.
Эти отрезки должны удовлетворять неравенствам треугольника, т.е. сумма двух сторон больше третьей:
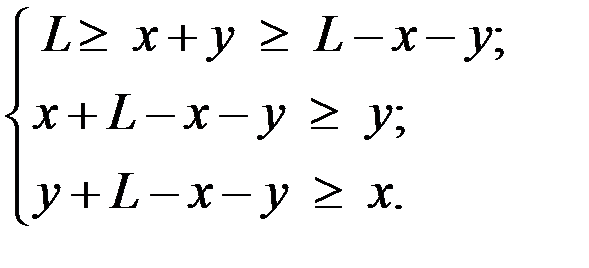
Сводим задачу к геометрической вероятности (рис.1.4):
| 
|
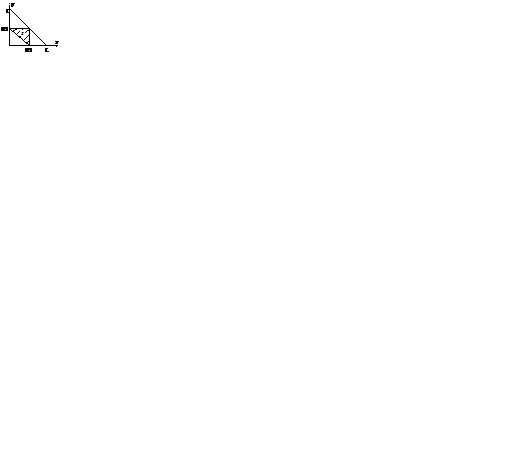
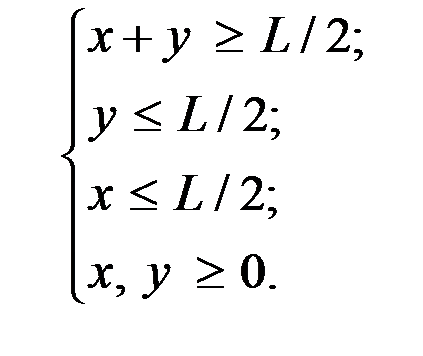
Рис. 1.4. Геометрическое представление задачи 1.33
Пример 1.34. Стрельба заканчивается после третьего попадания по мишени. Найти вероятность того, что при этом будет пять промахов, если вероятность попадания при одном выстреле равна 0,3.
Решение. Рассматриваемое событие наступит, если после 7 выстрелов было 2 попадания и восьмой выстрел был удачным. Следовательно,
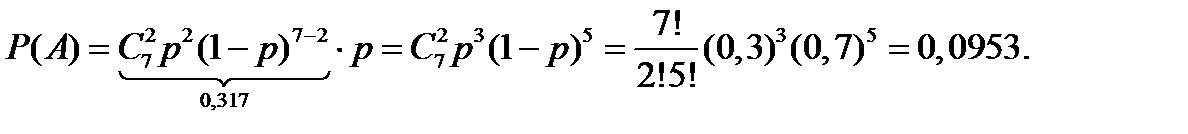
Пример 1.35. Какой толщины должна быть монета, чтобы вероятность её падения на ребро равнялась 1/3?
Решение. Рассмотрим сферу, и пусть монета вписана в эту сферу, центр которой совпадает с центром тяжести монеты. Сама монета при этом трактуется как прямой круговой цилиндр (рис. 1.5).
| 
| 
|
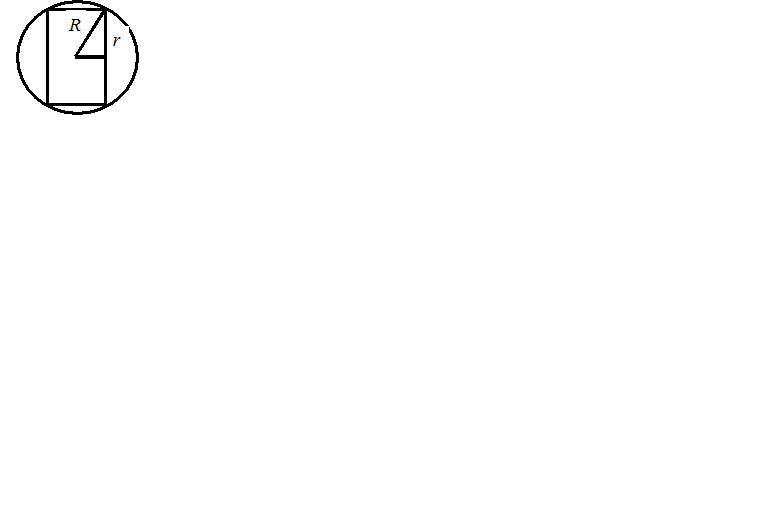
Рис. 1.5. Геометрическое представление задачи 1.35
На поверхности сферы выбирается случайная точка, и если радиус, проведённый из центра сферы в эту точку, пересекает боковую поверхность цилиндра, то считается, что монета упала на ребро.
Поверхность части сферы, заключённой между двумя параллельными плоскостями, пропорциональна расстоянию между этими плоскостями, так что толщина монеты должна составить 1/3 диаметра сферы.
Пусть R – радиус сферы, а r – радиус монеты.
Согласно теореме Пифагора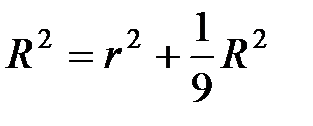 
или
.
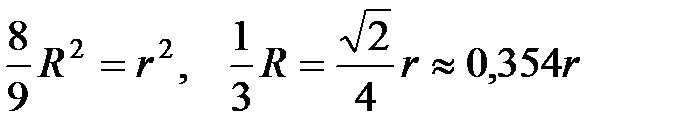Вывод: толщина монеты должна быть примерно равна 35% её диаметра, чтобы вероятность падения монеты на ребро равнялась бы 1/3.
Пример 1.36. В лифт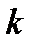 
–этажного дома ( 
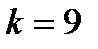) сели 
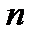пассажиров. Каждый ( 
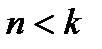) независимо от других с одинаковой вероятностью может выйти на любом этаже, начиная со второго. Определить вероятность того, что все пассажиры вышли на разных этажах.
Решение. Обозначим: событие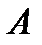 
– все вышли на разных этажах;
– 
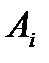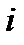–ый пассажир вышел на этаже, отличном от предыдущих.
Тогда событие А представляется в виде произведения
.
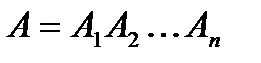Вероятности каждого события легко подсчитать непосредственно:
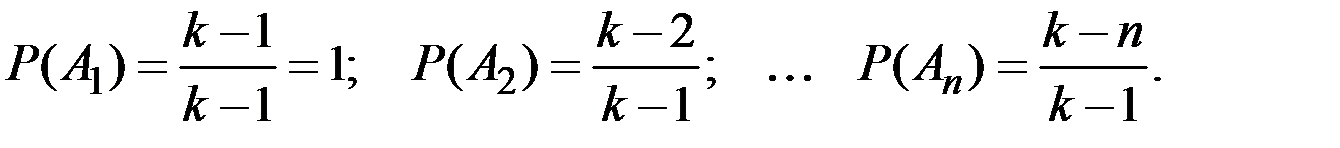
Тогда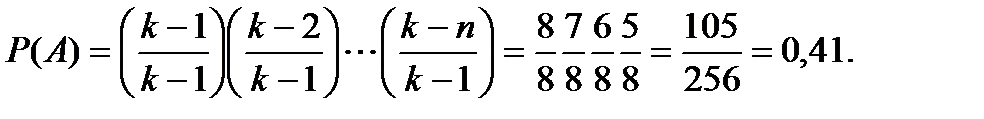 
Пример 1.37. Сотрудники предприятия полагают, что с вероятностью 80% ожидается рост спроса на их продукцию. Для уточнения ситуации предприятие обратилось к экспертам. Фирма, занимающаяся прогнозом рыночной ситуации, подтвердила предположение о росте спроса. Положительные прогнозы консультационной фирмы сбываются с вероятностью 95% , а отрицательные – с вероятностью 85%. Какова вероятность того, что рост спроса действительно произойдёт?
Решение. Обозначим:
A – событие: будет спрогнозирован рост спроса;
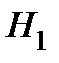– гипотеза: спрос возрастёт;
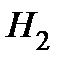– гипотеза: спрос упадёт.
По ожиданиям работников предприятия
; 
.
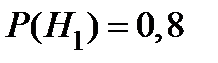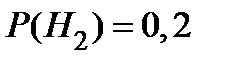Так как положительные прогнозы консультационной фирмы сбываются с вероятностью 95% , а отрицательные – с вероятностью 85%, то:
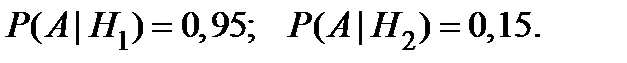
Вероятность события А вычисляется по формуле полной вероятности:
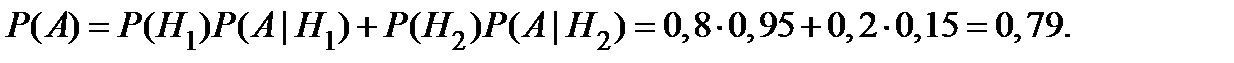
С учётом факта прогноза события A можно уточнить вероятность гипотезы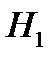 
по формуле Байеса:
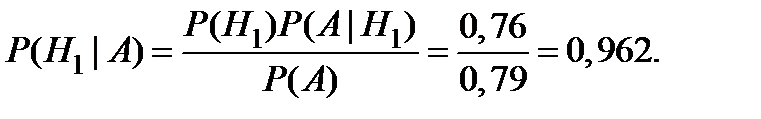
Пример 1.38. Задача Бюффона. На пол, разграфлённый параллельными линиями на полосы шириной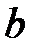 
, бросается наугад игла длины 
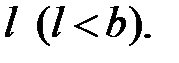Найти вероятность того, что игла пересечёт какую–нибудь прямую.
Решение. Расположение иглы определяется двумя случайными величинами: х – расстояние от центра иглы до ближайшей к нему прямо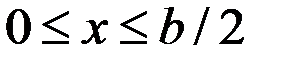й
( 
) и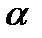 
– угол, составленный иглой с этой прямой ( 
).
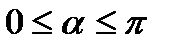Пересечение иглы прямой происходит, если выполняется условие
.
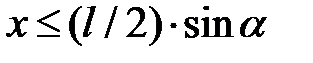Тогда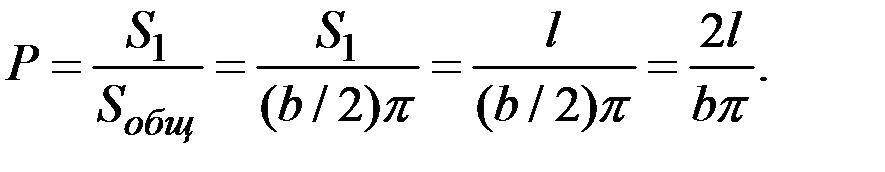 
Здесь
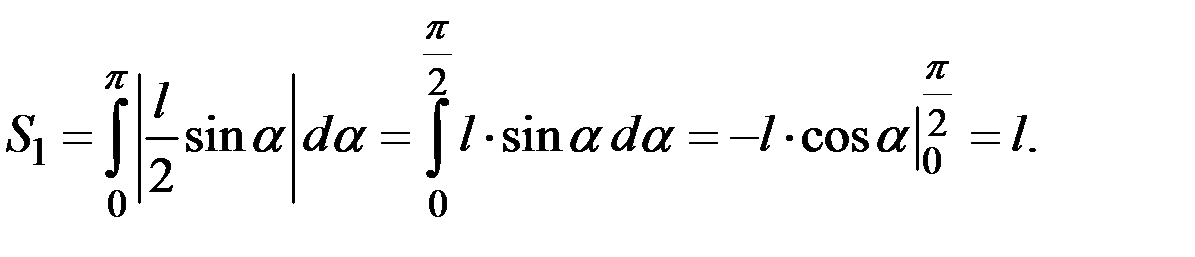
Пример 1.39. 15 экзаменационных билетов содержат по 2 вопроса, которые не повторяются. Студент может ответить только на 25. Определить вероятность того, что экзамен будет сдан, если для этого достаточно ответить на 2 вопроса из одного билета или на 1 вопрос из первого билета и дополнительный вопрос из другого билета.
Решение: Имеется всего 30 вопросов. Пусть:
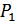– вероятность, что студент не знает ни одного вопроса в билете:
.
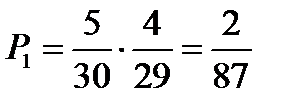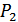– вероятность, что студент знает ответ на оба вопроса в билете:
.
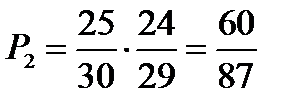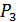– вероятность того, что студент знает один из вопросов:
.
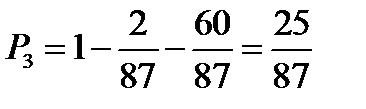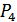– вероятность, что студент знает ответ на дополнительный вопрос.
Так как студент уже взял 1 билет и ответил на 1 вопрос из него, то:
.
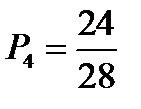Следовательно, экзамен будет сдан с вероятностью:
.
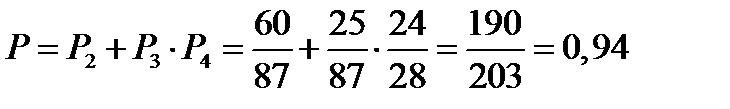Пример 1.40. 10 деталей, из которых 4 бракованных, разложили в случайном порядке в две упаковки по 5 штук. Найти вероятность того, что в каждой упаковке будет по 2 бракованные детали.
Решение. Используем комбинаторику:
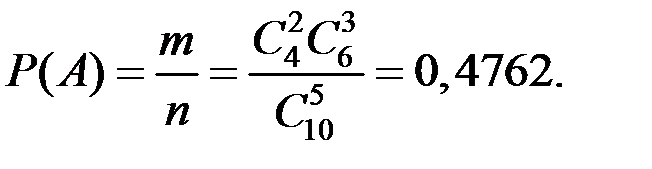
Сравним эту вероятность с приближённым расчётом по формуле Бернулли:
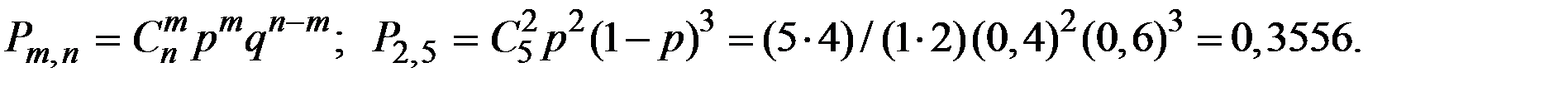
Пример 1.41. Среди 10 электрических лампочек 3 нестандартные. Найти вероятность того, что две одновременно взятые лампочки окажутся нестандартными.
Решение. Используем комбинаторику:
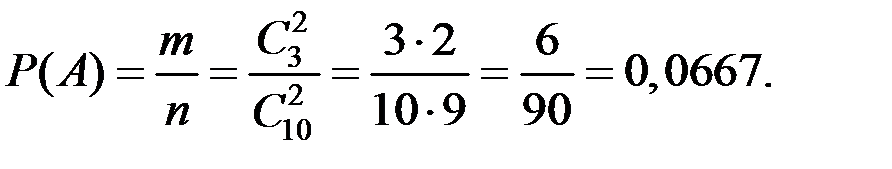
Пример 1.42. В группе 15 человек. Группу разделили на 3 подгруппы по 5 человек. Какова вероятность того, что два друга окажутся в одной подгруппе?
Решение. Пусть первый студент попал в какую то подгруппу с вероятность 1. Тогда вероятность того, что и второй туда попадёт случайно, определяется соотношением вакансий и оставшихся студентов:
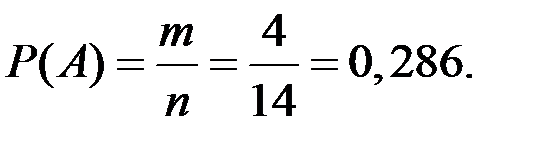
Пример 1.43. Пусть А, В, С и D – события, такие что
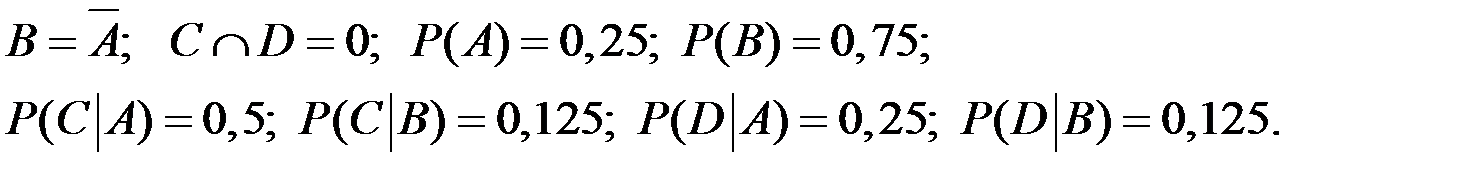
Определить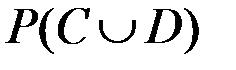 
.
Решение. По формуле полной вероятности получим вероятности
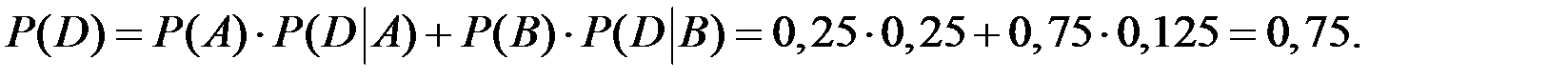
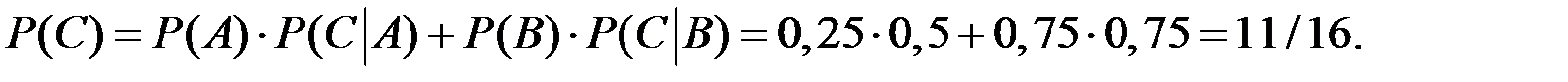
Тогда
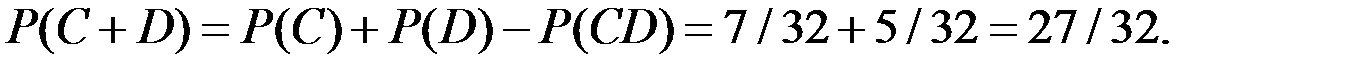
Пример 1.44. В ящике лежат 10 шаров, из которых 3 – красных, 2 – жёлтых и 5 голубых. Из ящика случайным образом, с возвращением, извлекается 5 шаров. Вычислить вероятность того, что менее двух извлечённых шаров – красные.
Решение. По формуле Бернулли
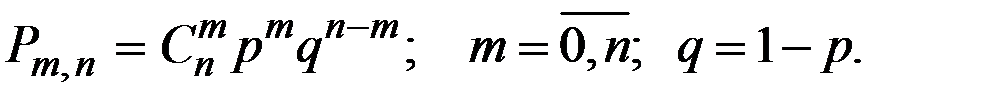
получаем
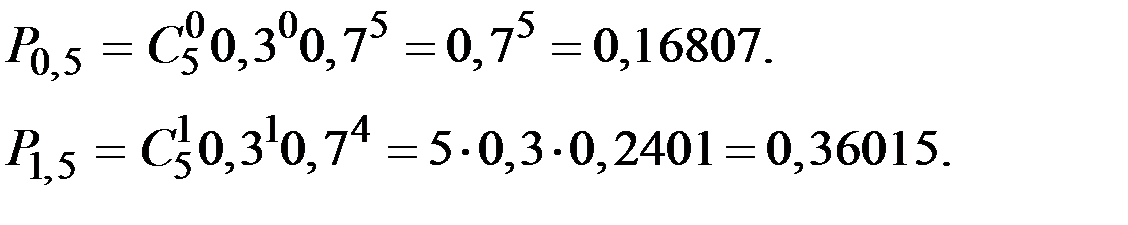
Тогда
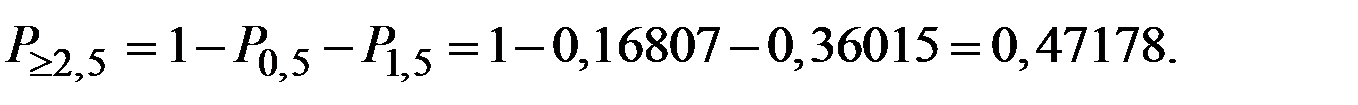
Пример 1.45. Вероятность наступления события в каждом опыте равна 0,2. Опыты производятся последовательно до наступления события. Определите вероятность того, что придётся производить четвёртый опыт.
Решение. Имеем произведение трёх событий с одинаковой вероятностью неудачи:
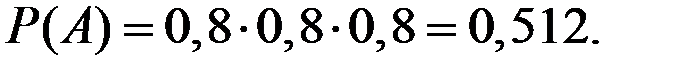
Пример 1.46. Из партии в 1000 автомобилей, собранных на конвейере 300 отправили в I зону, 150 во II, 150 в III, 300 в IV и 100 в V зону.
В I зоне после пробега 25 тысяч километров из 1000 автомобилей обычно из строя выходят 200, во II зоне – 300, в III – 350 и в IV – 250 и в V – 400. На завод поступило сообщение, что один из автомобилей данной серии вышел из строя. Определить вероятнейшую зону его отправки.
Решение. Используем формулу полной вероятности.
Можно сделать n исключающих друг друга предположений о зоне отправки авто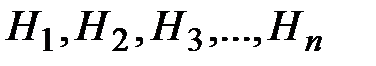 
. Событие 
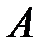(поломка авто) может появиться с каждой из этих гипотез.
Вероятность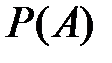 
вычисляется по формуле полной вероятности
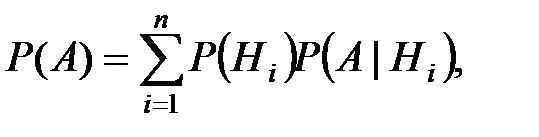
где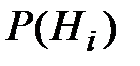 
– вероятность гипотезы 
;
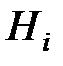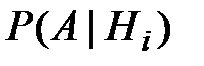– условная вероятность события A при гипотезе .
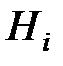Используя исходные данные получаем:
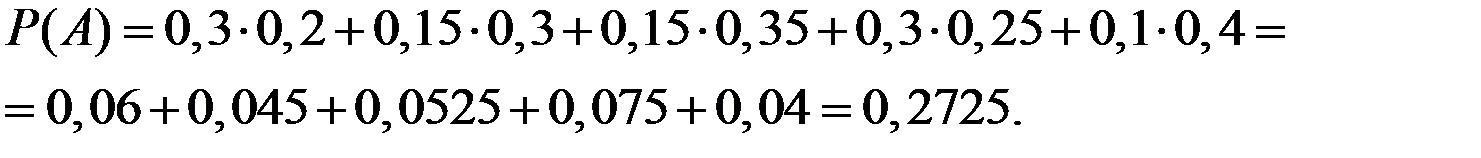
Вероятнейшая зона отправки сломанного авто – четвёртая.
Эта вероятность можно рассчитать по формуле Байеса:
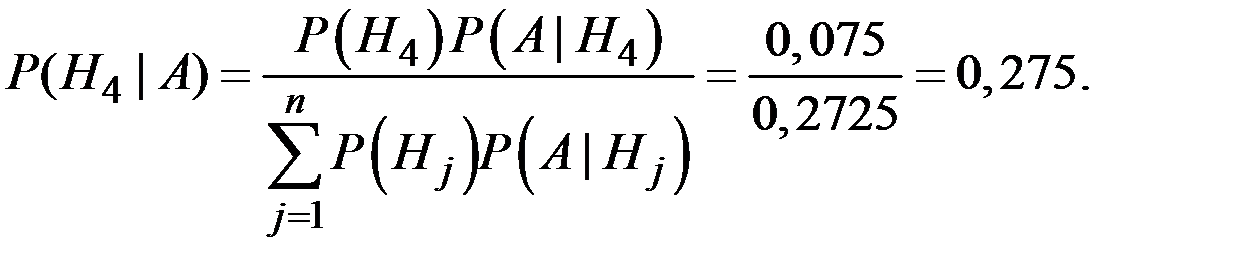
Пример 1.47. В ящике содержит 10 шаров. Из них 4 – красных и 6 – белых. Шары случайным образом извлекаются из ящика с возвращением, пока не будут извлечены 4 красных шара. Пусть X – число извлечённых белых шаров до тех пор, пока не был извлечён четвёртый красный шар. Определить вероятность P[X = 6].
Решение. Используем формулу Бернулли.
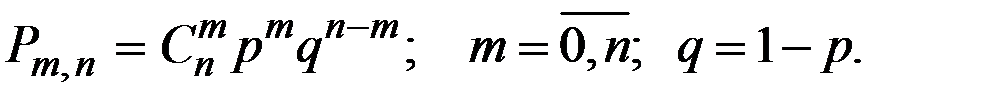
До извлечения последнего четвёртого красного шара должна быть ситуация, когда уже извлечено 3 красных шара и 6 белых. Тогда
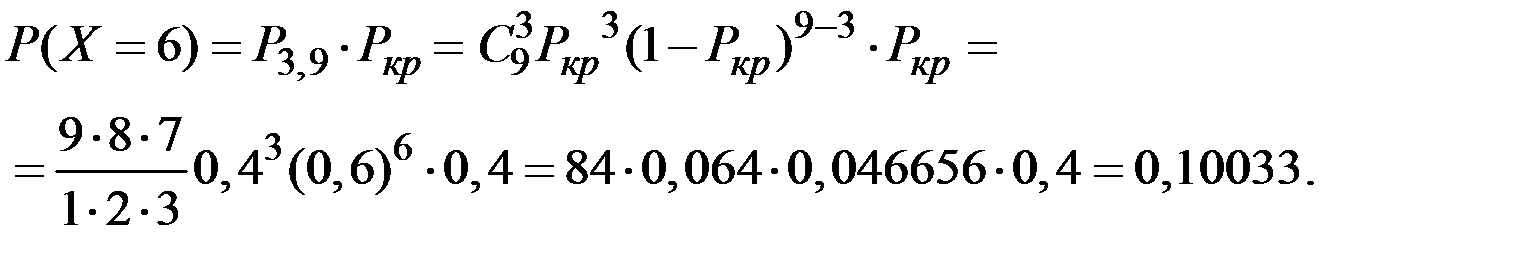
Пример 1.48. Пусть A и B – события, такие, что P[A] = 0,7 и P[B] = 0,9. Определить максимально возможную величину разности вероятностей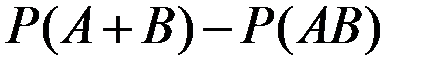 
.
Решение. Используем формулу вероятность суммы двух совместных событий
,
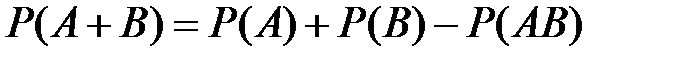где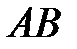 
– произведение событи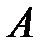й 
и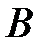 
.
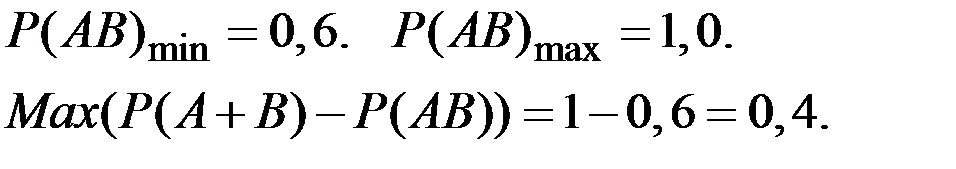
Пример 1.49. Какова вероятность увидеть (хотя бы одну) задуманную цифру (от 0 до 9) при случайнрм взгляде на электронные часы, показывающие часы (00–23) и минуты (00–59)?
Решение. Эта вероятность будет разной для различных задуманных цифр. Эту вероятность подсчитаем как дополнение к сложному событию А – все позиции (цифры) часов не содержат задуманной цифры.
Тогда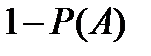 
– и есть искомая вероятность.
Для подсчета вероятности отсутствия задуманной цифры в соответствующем разряде часов используем формулу непосредственного подсчета вероятности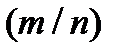 
, а отсутствие задуманной цифры в всех четырёх позициях часов используем формулу умножения зависимых событий.
Для цифр «0» и «1» искомая вероятность составит величину
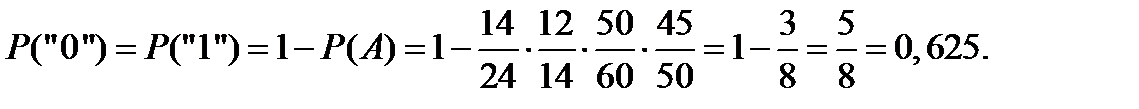
Для цифры «2» искомая вероятность составит величину
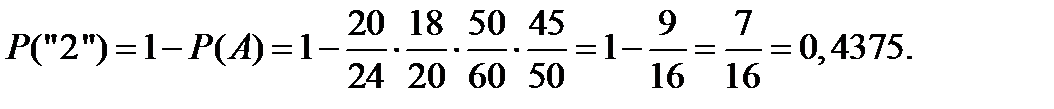
Для цифры «3» искомая вероятность составит величину
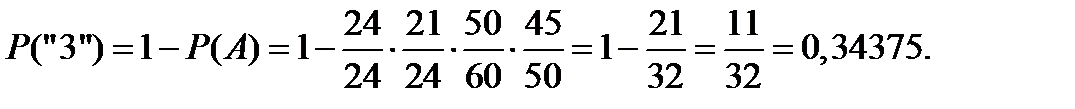
Для цифр «4» и «5» искомая вероятность составит величину
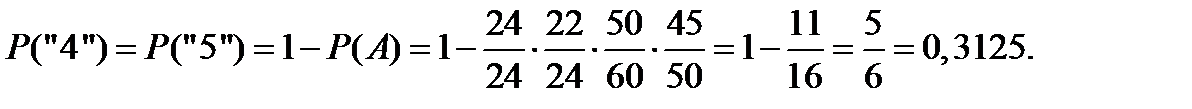
Для цифр «6», «7», «8», «9» искомая вероятность составит величину
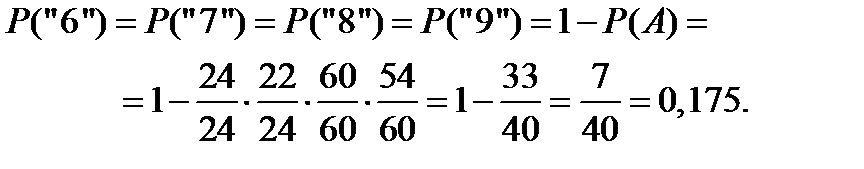
Пример 1.50. Телефонный номер состоит из 5 цифр. Найти вероятность того, что все цифры различны.
Решение. Задача на произведение событий. Вероятность того, что все цифры различны, образуется из того, что каждое из 5 – уникальная (неповторяющаяся) цифра. Причём безразлично, допустим «0» на первой позиции или нет. Получим:
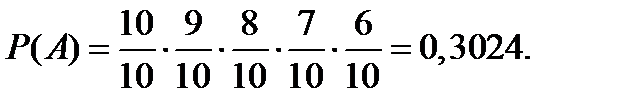
Пример 1.51. Магазин получил две равные по количеству партии одноимённого товара. Известно, что 25% первой партии и 40% второй партии составляет товар первого сорта. Какова вероятность того, что наугад выбранная единица товара будет не первого сорта?
Решение. Пусть:
A – событие, что достали деталь не первого сорта,
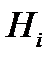– гипотеза, что достали деталь из i – й партии (i = 1,2).
Используем формулу полной вероятности:
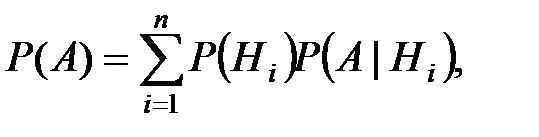
где 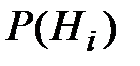– вероятность гипотезы ;
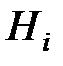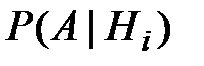– условная вероятность события A при гипотезе .
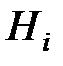Имеем:
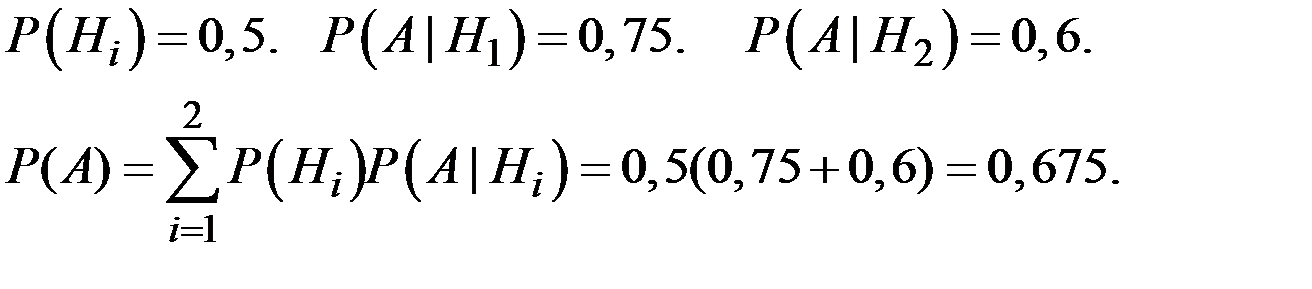
Пример 1.52. Производятся четыре выстрела по мишени. Вероятность попасть в цель при одном выстреле равна 0,29. Найдите вероятность того, что: 1) будет хотя бы одно попадание; 2) будет два попадания; 3) будет не менее трёх попаданий.
Решение. Используем формулу Бернулли. Если производится n независимых опытов в одинаковых условиях, причём в каждом из них с вероятностью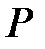 
может появиться событие A, то вероятность 
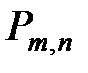того, что событие A произойдёт в этих n опытах ровно m раз, выражается формулой:
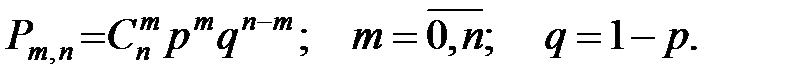
Тогда вероятность того, что будет не менее k попаданий определится соотношением:
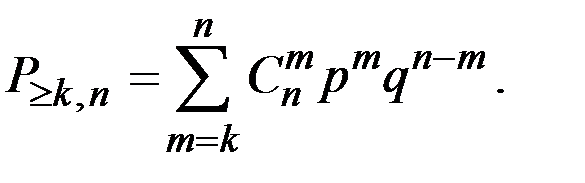
1. Вероятность того, что будет хотя бы одно попадание:
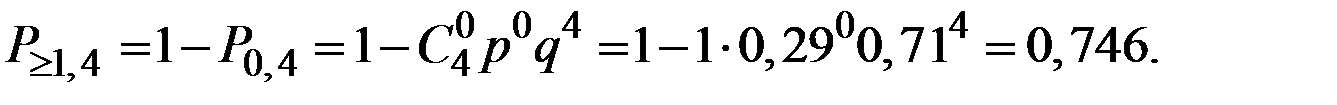
2. Вероятность того, что будет ровно два попадания:
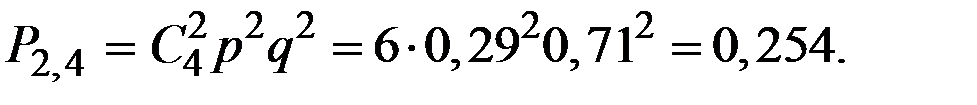
3. Вероятность того, что будет не менее трёх попаданий:
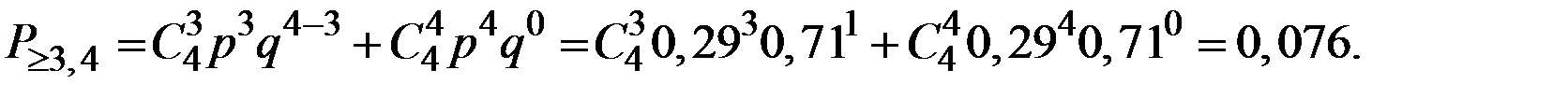
Пример 1.53. Бросаются два игральных кубика. Найти вероятность того, что сумма выпавших очков: 1) равна 7; 2) не превосходит 8; 3) больше 10.
Решение.
1. Число граней на игровом кубике равно 6.
Сумма выпавших очков на двух игральных кубиках может быть равна 7 в следующих комбинациях: (6,1); (5,2); (4,3); (3,4); (2,5); (1,6).
Всего 6 благоприятных комбинаций (m).
Всего же различных комбинаций (n) выпавших очков на двух игральных кубиках может быть равна 6∙6 = 36.
Тогда вероятность того, что сумма выпавших очков равна 7, определится соотношением:
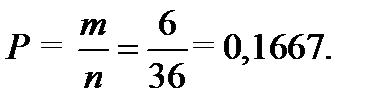
2. Вероятность того, что сумма выпавших очков не превосходит 8 определится аналогично, но благоприятных комбинаций (m) будет уже 26.
Неблагоприятными комбинациями будут следующие 10 из 36: (6,3); (6,4); (6,5); (6,6); (5,4); (5,5); (5,6); (4,5); (4,6); (3,6).
Тогда вероятность того, что сумма выпавших очков не превосходит 8, определится соотношением:
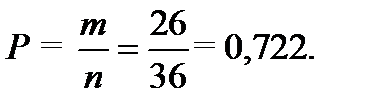
3. Вероятность того, что сумма выпавших очков больше 10 определится аналогично, но благоприятных комбинаций (m) будет только 4: (6,5); (6,6); (5,5); (5,6).
Тогда вероятность того, что сумма выпавших очков не превосходит 8, определится соотношением:
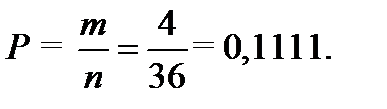
Пример 1.54. В ящике находится 8 гвоздей, 10 шурупов и 6 болтов. Наудачу выбирают две детали. Найдите вероятность того, что достали:
1) два болта; 2) два шурупа; 3) гвоздь и болт; 4) болт и шуруп.
Решение. Всего деталей в ящике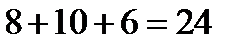 
.
1) Вероятность того, что первая взятая деталь – болт равна:
6/24 = 0,25.
Вероятность того, что и вторая взятая деталь – болт равна:
5/23 = 0,2174.
В итоге получаем вероятность того, что достали подряд два болта умножением вероятностей событий:
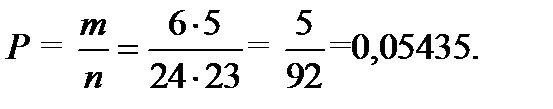
2) Вероятность того, что первая взятая деталь – шуруп:
10/24 = 0,4167.
Вероятность того, что и вторая взятая деталь – шуруп равна:
9/23 = 0,3913.
В итоге получаем вероятность того, что достали подряд два болта умножением вероятностей событий:
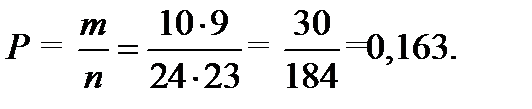
3) Вычислим вероятность того, что достали гвоздь и болт.
Получим два варианта события: достали сначала гвоздь, вероятность этого: 8/24, затем болт, вероятность этого: 6/23 или сначала болт с вероятностью: 6/24, затем гвоздь сначала болт с вероятностью: 8/23.
Тогда получим вероятность того, что достали гвоздь и болт:
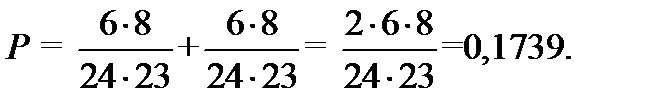
4) Вычислим вероятность того, что достали болт и шуруп.
Аналогично пункту 3 имеем два варианта события: достали сначала болт: 6/24, затем шуруп: 10/23 и сначала шуруп: 10/24, затем болт: 6/23.
Получаем итоговую вероятность:
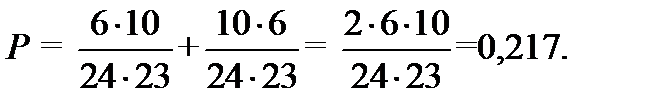
Пример 1.55. Имеются 2n шаров с числами от 1 до n. Каждое число встречается по 2 раза. Шары случайно располагаются по два в n ящиков. Из каждого ящика вынимается один шар. Какова вероятность того, что на взятых шарах все числа различные?
Решение. Всего можно организовать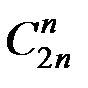 
вариантов взятия n шаров из 2n имеющихся шаров. Благоприятными исходами будут те случаи, когда все числа различные. Это количество определяется произведением n сочетаний:
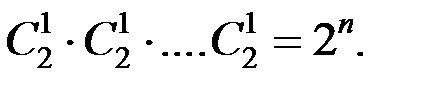
Тогда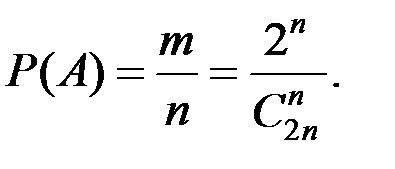 
Произведём расчёты для различных n.
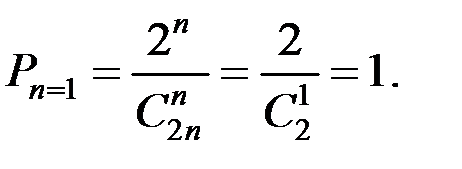
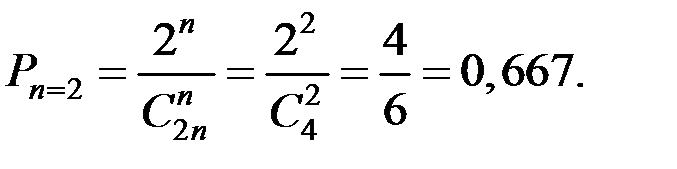
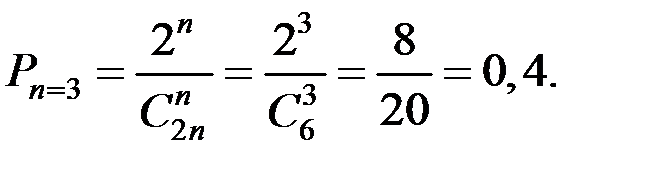
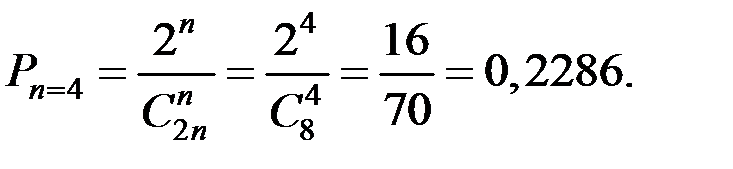
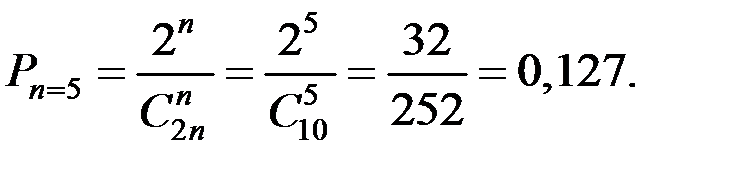
Эту же вероятность можно получить и через произведение вероятностей событий:
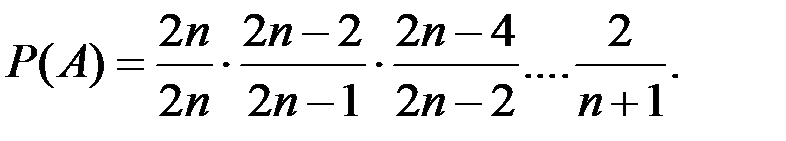
Пример 1.56. Устройство состоит из 12 независимых блоков, помеченных Б1, Б2, …, Б12. Вероятность того, что неисправность может произойти в одном из блоков Б1, Б2, Б3, Б4 составляет 0,6. При поиске появившейся неисправности обследованы блоки Б1, Б2, Б3, но неисправность не обнаружена. Какова вероятность того, что неисправность будет обнаружена в блоке Б4?
Решение. Обследование блоков Б1, Б2, Б3 привело к тому, что общая оставшаяся неопределённость оценивается вероятностью
1 – 3(0,6/4) = 0,55.
«Благоприятная» вероятность для рассматриваемого события из неё равна 0,15. Тогда
