– условная вероятность события A при гипотезе .
Если до опыта вероятности гипотез были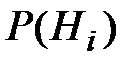 
, а в результате опыта появилось событие A, то с учётом этого факта условные вероятности гипотез вычисляются по формуле Байеса:
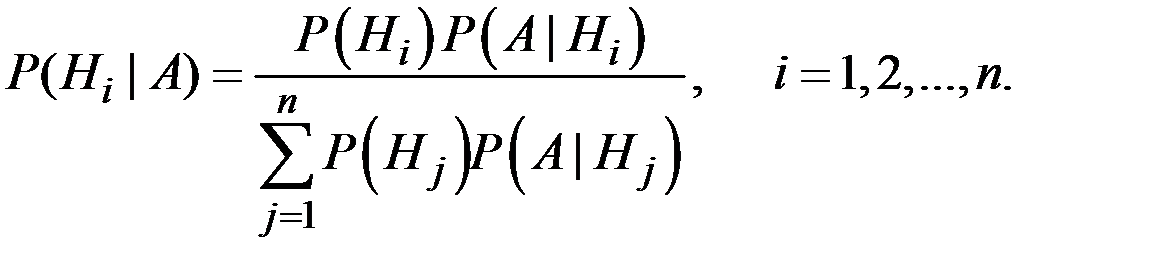
Формула Байеса даёт возможность "пересмотреть" вероятности гипотез с учётом полученного результата опыта.
Если после опыта, заканчивающегося появлением события A, производится ещё один опыт, в котором может появиться или не появиться событие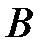 
, то условная вероятность этого последнего события вычисляется по формуле полной вероятности, в которую подставлены не прежние вероятности гипотез 
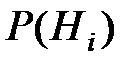, а новые 
:
.
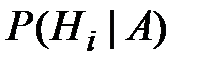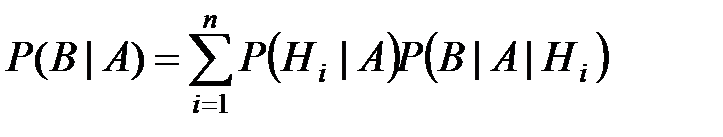Пример 1.16. Вероятность выхода прибора из строя в нормальном режиме работы равна 0,1, а в аварийном – 0,7. Вероятность нормального режима работы – 0,8, аварийного – 0,2. Определить вероятность выхода прибора из строя. Прошло время, прибор сгорел. Какова вероятность того, что были перегрузки (аварийный режим)?
Решение. Из условия задачи формулируем гипотезы:
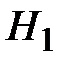– прибор работает в нормальном режиме;
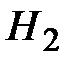– прибор работает в аварийном режиме.
Пусть A событие, означающее, что прибор вышел из строя.
Имеем: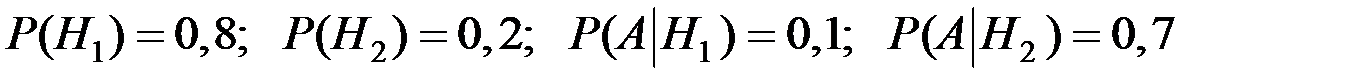 
.
Тогда по формуле полной вероятности получаем:
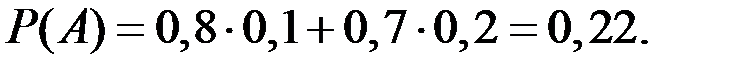
По формуле Байеса можно вычислить вероятность второй гипотезы:
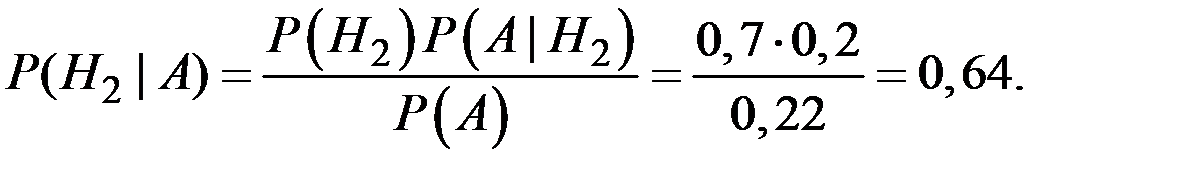
Пример 1.17. В первой группе 28 человек, а во второй – 15. Во второй группе все получили зачёт, а впервой – только 21 человек. Первый встретившийся студент группы имеет зачёт. Определить вероятность того, что он из первой группы.
Решение. Обозначим:
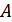– событие, студент имеет зачёт.
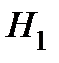– гипотеза: студент из первой группы.
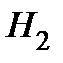– гипотеза: студент из второй группы партии.
Имеем в силу разной численности групп:
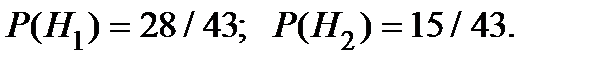
Вероятность события А найдём по формуле полной вероятности:
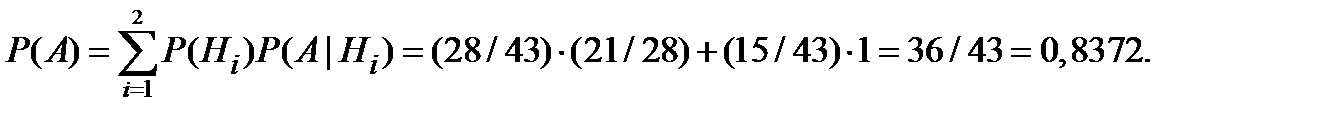
С учётом свершения события А уточним вероятность гипотезы 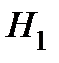по формуле Байеса:
Пример 1.18. В альбоме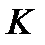 
чистых и 
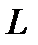гашёных марок. Из них наудачу извлекаются 
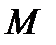марок, подвергаются спецгашению и возвращаются в альбом. После этого вновь наудачу извлекаются 
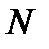марок. Определить вероятность того, что все 
марок чистые.
Решение. Обозначим:
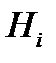– гипотеза, на спецгашение взято 
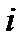чистых марок и 
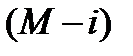гашеных, где 
;
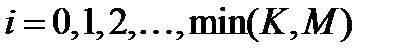Событи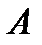е 
– все марок чистые.
Тогда искомую вероятность того, что все 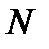марок чистые, определим по формуле полной вероятности:
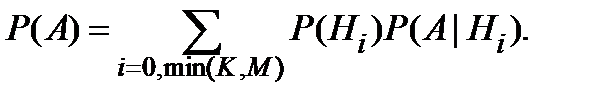
Здесь
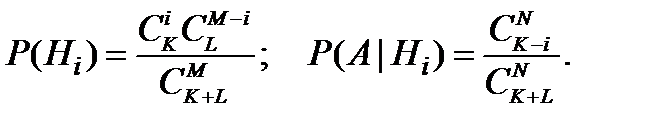
1.5. Повторение опытов
Опыты называются независимыми, если вероятность исхода (результата) каждого опыта не зависит от того, какие исходы имели другие опыты. Независимые опыты могут проводиться как в одинаковых условиях, так и в различных. В первом случае вероятность появления какого–то события A во всех опытах одна и та же, во втором случае она меняется от опыта к опыту.
Если производится n независимых опытов в одинаковых условиях, причём в каждом из них с вероятностью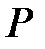 
может появиться событие A, то вероятность 
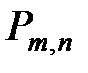того, что событие A произойдёт в этих n опытах ровно m раз, выражается формулой Бернулли:
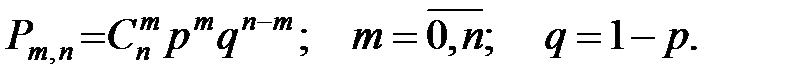
Это биномиальное распределение вероятностей.
Вероятность хотя бы одного появления события A в n независимых опытах в одинаковых условиях равна
.
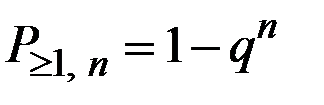Если производится n независимых опытов в различных условиях, причём вероятность события А в 
опыте равна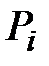 
, то вероятность 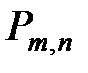того, что событие 
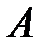появится в этих n опытах ровно 
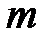раз, равна коэффициенту при 
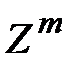в разложении по степеням 
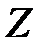производящей (вычислительной, вспомогательной) функции
.
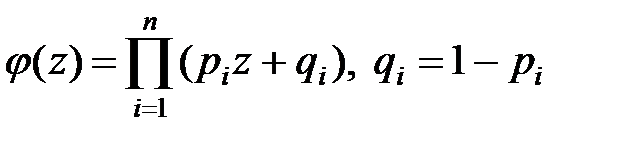Вероятность хотя бы одного появления события A в n независимых опытах в различных условиях равна
.
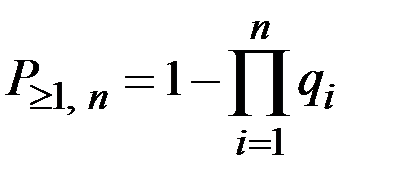Для любых условий опыта
.
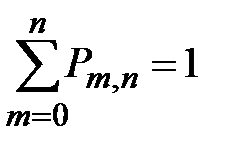Вероятность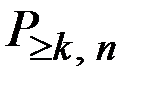 
того, что в n опытах событие А появится не менее 
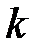раз, выражается формулой:
.
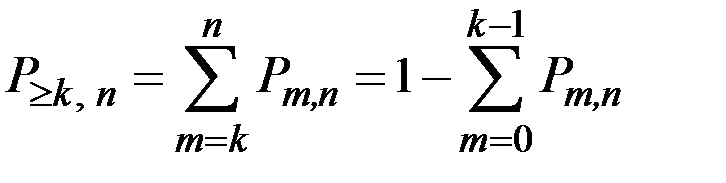