Событие называется противоположным событию A, если оно состоит в непоявлении события A.
Пример 1.10. В ящике 2 белых и 1 чёрный шар. Рассматриваются 2 события: А – первый студент взял белый шар; В – второй студент взял белый шар. Зависимы ли события А и В?
Решение. Вычислим условные и безусловные вероятности событий.
Имеем:
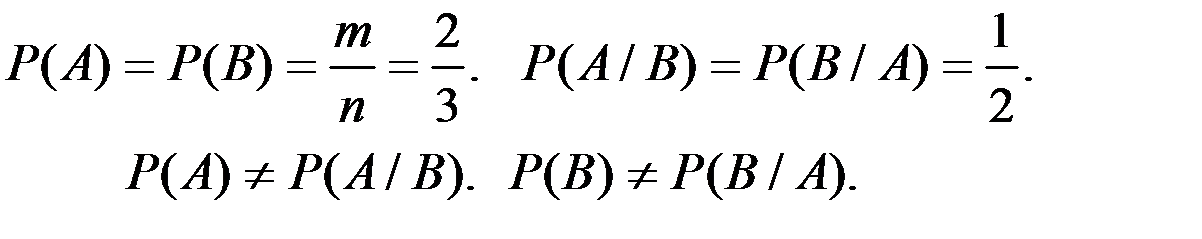
События А и В зависимы.
Вероятность суммы любого числа совместных событий определяется зависимостью
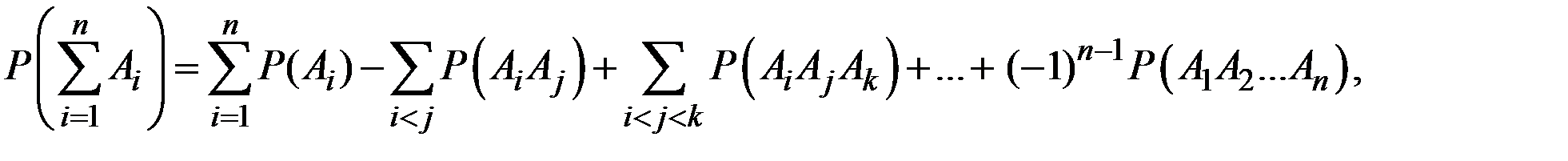
где суммы распространяются на различные сочетания соответствующих индексов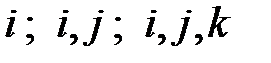 
и т.д.
В частном случае, вероятность суммы двух совместных событий
,
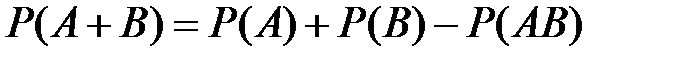где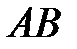 
– произведение событи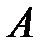й 
и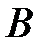 
.
В общем случае для несовместных событий имеем соотношение
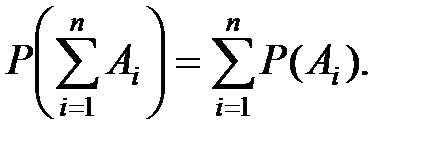
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:
.
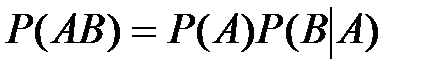Для двух независимых событий имеем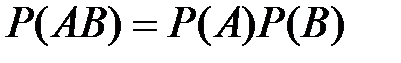 
.
Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причём вероятность каждого следующего по порядку вычисляется при условии, что все предыдущие имели место:
.
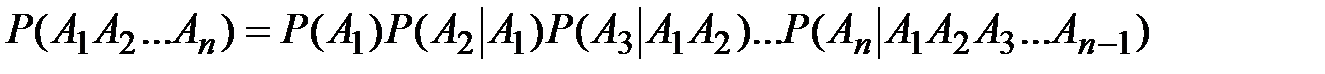Вероятность произведения независимых событий равна произведению вероятностей этих событий:
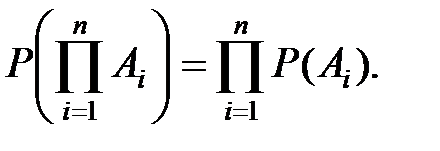
Примечание. Во многих задачах сложное событие раскладывается на простейшие, и применяются формулы вероятностей суммы и произведения событий а также формула непосредственного подсчёта вероятностей.
Пример 1.11. Какова вероятность вытащить два разноцветных шара, если в ящике a белых и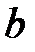 
черных шаров?
Решение. Пусть событие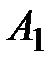 
– 1–й шар белый, 
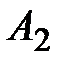– 2–й шар чёрный; 
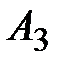– 1–й шар чёрный, 
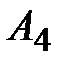– 2–й шар белый.
Тогда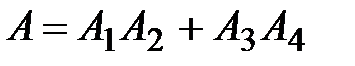 
.
Следовательно:
.
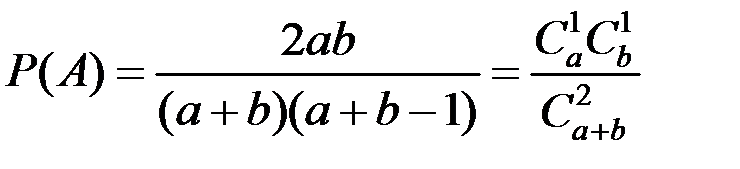Пример 1.12. Студент знает 40 из 50 вопросов программы. Найти вероятность того, что студент знает 2 вопроса, содержащихся в его экзаменационном билете.
Решение. Представим сложное событие A как произведение двух событий
,
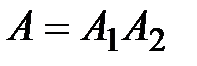где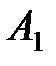 
– студент знает 1–й вопрос, 
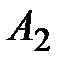– студент знает 2–й вопрос.
Тогда вероятность того, что студент знает оба вопроса
.
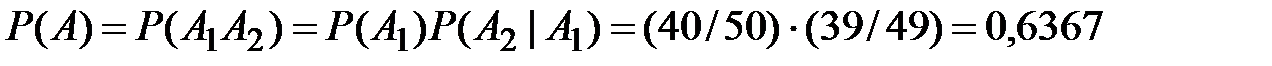Если в экзаменационном билете 3 вопроса, то вероятность того, что студент знает все 3 вопроса
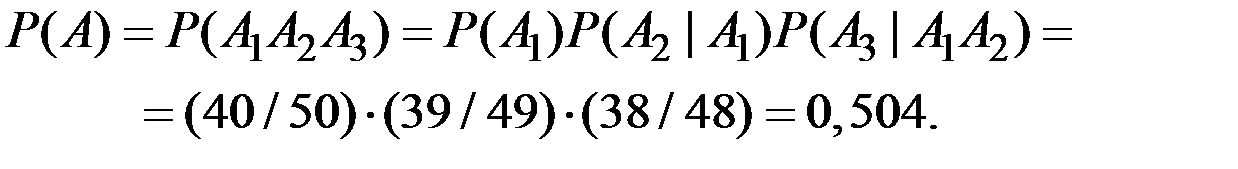
Пример 1.13. Вероятность сдачи зачёта за одну попытку равна 0,3 и не зависит от номера попытки. Какова вероятность того, что студент придёт сдавать зачёт в четвёртый раз? Какова вероятность того, что студент сдаст зачёт ровно с четвёртой попытки?
Решение. Для ответа на первый вопрос используем формулу умножения трёх событий: не сдал первый раз; не сдал второй раз; не сдал третий раз (вынужден прийти в четвёртый раз):
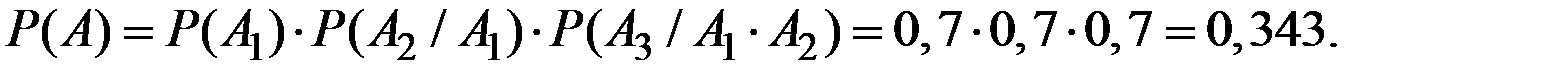
Вероятность того, что студент сдаст зачёт ровно с четвёртой попытки, определяется вероятностями двух событий: надо прийти четвёртый раз и сдать зачёт за эту попытку:
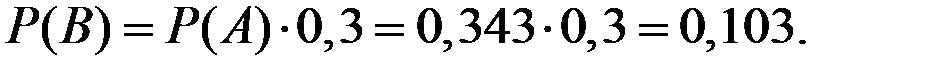
Пример 1.14. Какова вероятность взять сразу 4 карты разной масти из колоды в 36 карт?
Решение. Используем формулу умножения четырёх событий.
Пусть событие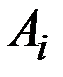 
означает, что i –ая карта удовлетворяет рассматриваемому событию. Тогда искомая вероятность определится по формуле умножения зависимых событий:
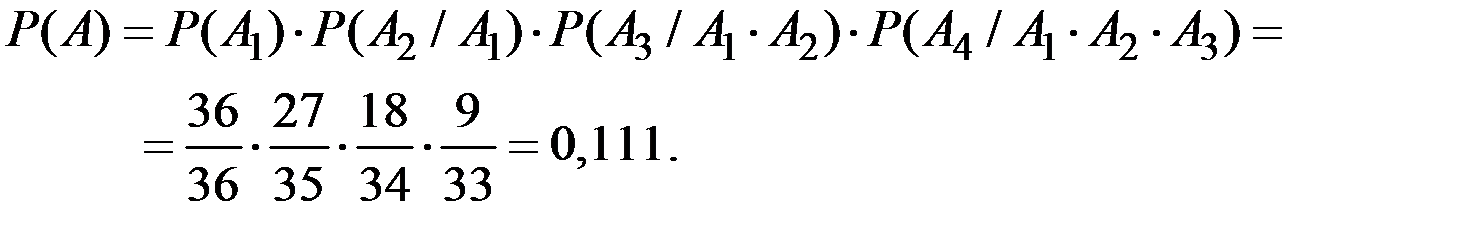
Пример 1.15. Фирма претендует на два заказа от двух корпораций А и В. Эксперты фирмы считают, что вероятность получения заказа от корпорации А равна 0,45. Эксперты так же полагают, что если фирма получит заказ у корпорации А, то вероятность того, что и корпорация В обратится к ним, равна 0,9. Какова вероятность того, что фирма получит оба заказа?
Решение. Имеем произведение двух событий.
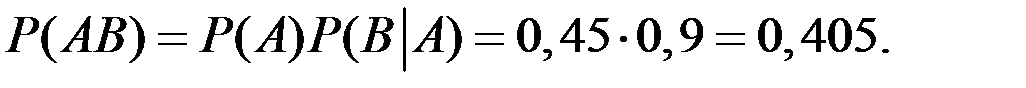
1.4. Формула полной вероятности и формула Байеса
Если об обстановке (условиях) опыта можно сделать n исключающих друг друга предположений (гипотез)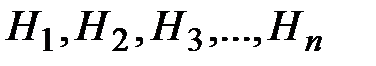 
и если событие 
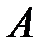может появиться с каждой из этих гипотез, то 
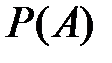вычисляется по формуле полной вероятности
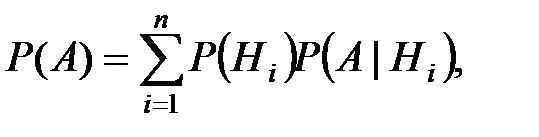
где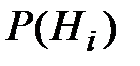 
– вероятность гипотезы 
;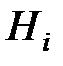