Пример 1.9. Парадокс Бертрана. В круге радиуса случайно проводится хорда. Найти вероятность того, что длина этой хорды больше числа Х.
Решение.
Вариант 1 (рис. 1.2). Хорды, пересекающие малый (заштрихованный) круг, будут больше X.
Следовательно, искомая вероятность может быть определена как отношение площади малого круга к площади большого круга:
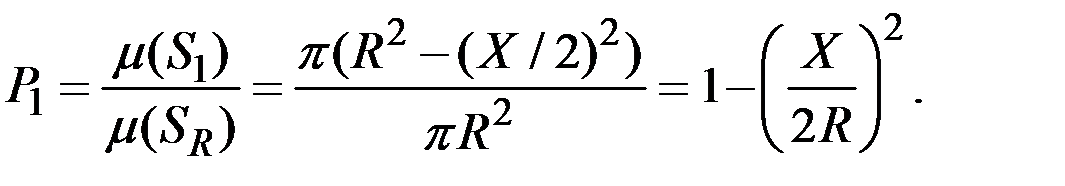
Рис. 1.2. Геометрическая интерпретация задачи Бертрана
Вариант 2. Хорды, перпендикулярно пересекающие выделенный участок диаметра, будут больше Х.
Следовательно, искомая вероятность может быть определена как отношение длины выделенного участка диаметра ко всему диаметру круга:
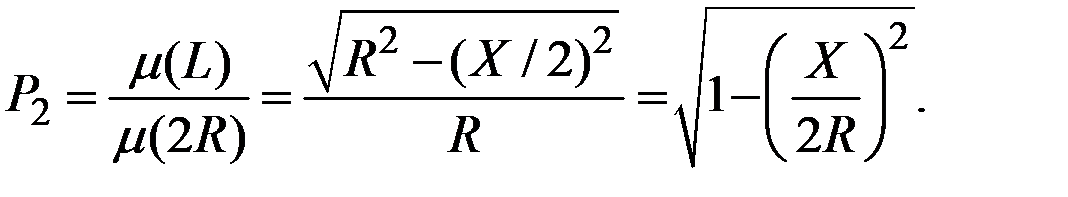
Вариант 3. Закрепим один конец хорды в точке А. Тогда все хорды, находящиеся в угле a, будут иметь длину, большую Х.
Следовательно, искомая вероятность может быть определена как отношение длины дуги, образующей угол a, и полной длины окружности, т.е.
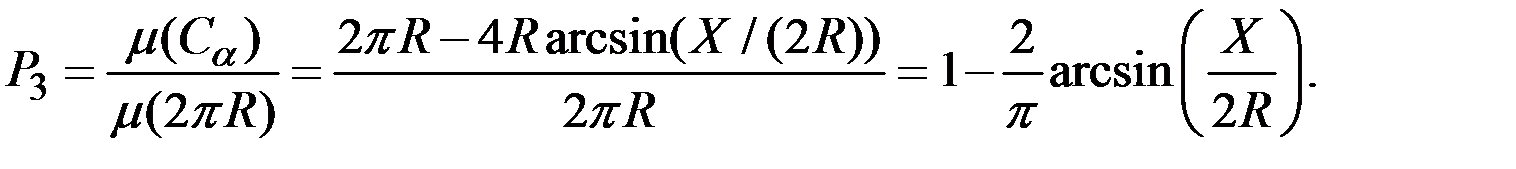
Получили три различных решения одной и той же задачи.
Здесь важны нюансы слова «случайно».
В варианте 1 середина хорды равномерно распределена в круге.
Второй вариант решения отражает ситуацию, когда задано направление хорды, а её середина равномерно распределена на диаметре, перпендикулярном её направлению.
В третьем варианте один конец хорды закреплён, а второй конец хорды равномерно распределён на окружности.
В различных вариантах решения используется различная мера, что и даёт соответствующие результаты.
1.3. Теоремы сложения и умножения вероятностей
Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.
Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Событие A 
называется независимым от события В, если вероятность события A не зависит от того, произошло событие В или нет.
Событие A называется зависимым от события B, если вероятность события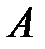 
меняется в зависимости от того, произошло событие В или нет.
Если событие A не зависит от события В, то и событие В не зависит от события A.
Вероятность события A, вычисленная при условии, что имело место другое событие B, называется условной вероятностью события A и обозначается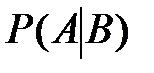 
.
Условие независимости события A от события В можно записать в виде
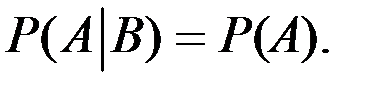
Условие зависимости определяется соотношением
.
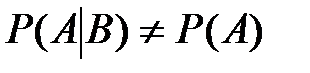