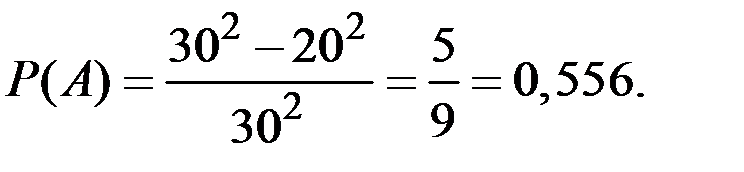Любое случайное событие отождествляется с некоторым подмножеством множества и интерпретируется как попадание элементов события в множество .
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное
Учреждение высшего образования
«Тульский государственный университет»
Институт прикладной математики и компьютерных наук
А.А. КОЧЕТЫГОВ
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
УЧЕБНОЕ ПОСОБИЕ
Тула
Издательство ТулГУ
2016
УДК 519.21 (075.8)
ББК 22.171 Я73
К75
| Рецензенты: | кафедра алгебры, математического анализа и геометрии ФГБОУ ВПО «Тульский государственный педагогический университет им. Л.Н. Толстого» (зав. кафедрой д–р физ.–мат. наук, проф. Н.М. Добровольский); |
| доктор физ.–мат. наук, доцент Тульского государственного университета Христич Д.В. |
Кочетыгов А.А. Теория вероятностей: учеб. пособие / – Тула, Изд–во ТулГУ, 2016. – 234 с.
ISBN 9785–7679–3647–2
Даётся взаимосвязанное изложение основных сведений о математическом инструментарии количественного описания случайных событий, величин, процессов, их функций и систем. Приводятся данные об основных количественных характеристиках моделирования стохастических явлений (событий, величин, процессов) и особенностях их применения. Основные понятия иллюстрируются многообразными примерами прикладного содержания и заданиями для самостоятельной работы.
Пособие предназначено для студентов направлений "Прикладная математика и информатика", "Механика и математическое моделирование", а также может быть полезно студентам, магистрам, аспирантам других направлений и специальностей, изучающих вопросы практического использования современных вероятностных методов в различных областях деятельности.
Табл. 19. Ил. 24. Библиогр.: 35 назв.
Печатается по решению библиотечно–издательского совета Тульского государственного университета
| © | А.А. Кочетыгов, 2016 | |
| ISBN 9785–7679–3647–2 | © | Издательство ТулГУ, 2016 |
СОДЕРЖАНИЕ
| ВВЕДЕНИЕ .................................................................................. | 5 | |
| 1. | СЛУЧАЙНЫЕ СОБЫТИЯ ......................................................... | 7 |
| 1.1. | Элементарные понятия случайных событий ............................ | 7 |
| 1.2. | Аксиоматический подход в теории вероятностей ................... | 11 |
| 1.3. | Теоремы сложения и умножения вероятностей ....................... | 15 |
| 1.4. | Формула полной вероятности и формула Байеса .................... | 18 |
| 1.5. | Повторение опытов ..................................................................... | 20 |
| 1.6. | Решение типовых задач главы 1 ……………………………… | 23 |
| 2. | СЛУЧАЙНЫЕ ВЕЛИЧИНЫ ...................................................... | 46 |
| 2.1. | Описание случайных величин .................................................... | 46 |
| 2.2. | Числовые характеристики случайных величин ....................... | 50 |
| 2.3. | Основные законы распределения ............................................... | 59 |
| 2.4. | Решение типовых задач главы 2 ……………………………… | 71 |
| 3. | СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН .................................... | 97 |
| 3.1. | Система двух случайных величин ............................................. | 97 |
| 3.2. | Условные законы распределения .............................................. | 100 |
| 3.3. | Числовые характеристики системы двух величин ................... | 103 |
| 3.4. | Система произвольного числа случайных величин ................. | 107 |
| 3.5. | Числовые характеристики системы нескольких величин ....... | 109 |
| 3.6. | Нормальный закон распределения системы двух величин …. | 110 |
| 3.7. | Решение типовых задач главы 3 ……………………………… | 113 |
| 4. | ФУНКЦИИ СЛУЧАЙНЫХ ВЕЛИЧИН .................................... | 121 |
| 4.1. | Законы распределения функций случайных величин ............. | 121 |
| 4.2. | Числовые характеристики функций случайных величин ....... | 124 |
| 4.3. | Композиция законов распределения ......................................... | 128 |
| 4.4. | Решение типовых задач главы 4 ……………………………… | 133 |
| 5. | ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ ...... | 141 |
| 5.1. | Закон больших чисел .................................................................. | 141 |
| 5.2. | Центральная предельная теорема .............................................. | 145 |
| 5.3. | Решение типовых задач главы 5 ……………………………… | 150 |
| 6. | ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ СЛУЧАЙНЫХ ВЕЛИЧИН ……………………………………………………... | 157 |
| 6.1. | Определение и свойства характеристической функции ........... | 157 |
| 6.2. | Использование характеристических функций ......................... | 161 |
| 6.3. | Семиинварианты ......................................................................... | 164 |
| 7. | СЛУЧАЙНЫЕ ПРОЦЕССЫ ………………………………….. | 167 |
| 7.1. | Основные понятия и характеристики случайных процессов .. | 167 |
| 7.2. | Стационарные случайные процессы ………………………….. | 176 |
| 7.3. | Система случайных функций …………………………………. | 183 |
| 7.4. | Преобразования случайных процессов ………………………. | 189 |
| 7.5. | Выбросы случайных процессов ………………………………. | 202 |
| 7.6 | Спектральное представление стационарных процессов ……. | 211 |
| БИБЛИОГРАФИЧЕСКИЙ СПИСОК ………………………… | 227 | |
| ПРИЛОЖЕНИЕ. СПРАВОЧНЫЕ ТАБЛИЦЫ ДЛЯ РАСЧЁТОВ …...…………. | 229 |
ВВЕДЕНИЕ
Во многих областях своей практической деятельности человек сталкивается с явлениями, на которые оказывают влияние множество факторов, не поддающиеся строгому учёту и контролю. Объективное суждение о закономерностях таких процессов возможно лишь на основе вероятностно–статистического анализа. Изучением закономерностей случайных массовых явлений и занимается особая математическая наука – теория вероятностей. Раздел теории вероятностей, изучающий методы обработки результатов опытов и получения из них обоснованных научных и практических выводов, называется математической статистикой.
Область практического применения теории вероятностей непрерывно расширяется. Сейчас трудно назвать отрасль науки или практики, которая не пользовалась бы вероятностными методами. Современный специалист должен хорошо ориентироваться в вопросах количественного описания вероятностных процессов, оценивать закономерности в случайных явлениях, владеть навыками обработки статистических данных, уметь перевести задачу с проблемно–содержательного языка на язык абстрактных математических схем и моделей.
Цель пособия – дать студентам систематическое и взаимосвязанное изложение основных сведений о математическом инструментарии количественного описания стохастических явлений и процессов, а также привить навыки использования этих знаний к решению практических задач.
В пособии приводятся необходимые теоретические сведения, математический аппарат решения задач, применение которого иллюстрируется решением типовых примеров. В конце каждого раздела предлагаются контрольные задачи и индивидуальные задания для закрепления соответствующего материала.
В конце пособия приводятся образцы справочные таблицы для выполнения статистических расчётов.
Более подробную информацию по затронутым вопросам можно получить из приводимого библиографического списка.
Пособие предназначено для студентов направлений "Прикладная математика и информатика", "Механика и математическое моделирование", а также может быть полезно студентам, магистрам, аспирантам других направлений и специальностей, изучающих вопросы практического использования современных вероятностных методов в различных областях деятельности.
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
| P(A) | – | вероятность случайного события А; |
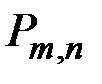
| – | вероятность того, что случайное событие произойдёт ровно m раз в n опытах; |
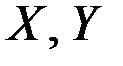
| – | случайные величины (наименования); |
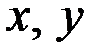
| – | значения случайных величин; |
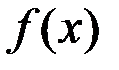
| – | функция плотности распределения вероятностей случайной величины Х; |
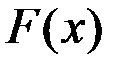
| – | функция распределения вероятностей величины Х; |
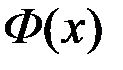
| – | функция Лапласа 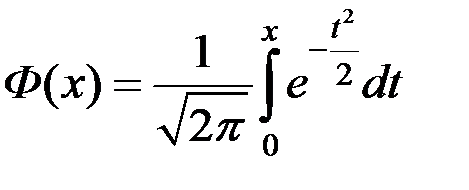 ; ;
|
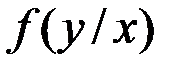
| – | условная функция плотности распределения вероятностей случайной величины Y при условии, что величина Х принимает значение х; |
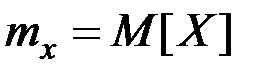
| – | математическое ожидание случайной величины Х; |
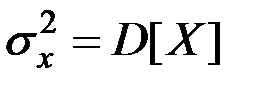
| – | дисперсия случайной величины Х; |
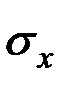
| – | среднее квадратическое отклонение величины Х; |
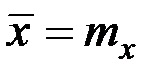
| – | среднее значение случайной величины Х; |
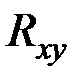
| – | корреляционный (ковариационный) момент случайных величин Х и Y; |
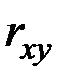
| – | коэффициент линейной корреляции показателей Х и Y; |
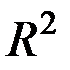
| – | коэффициент детерминации; |
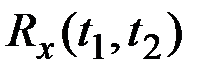
| – | автокорреляционная функция процесса X(t), АКФ; |
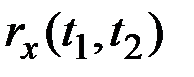
| – | нормированная корреляционная функция X(t); |
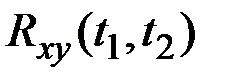
| – | взаимная корреляционная функция процессов X(t) и Y(t) (ВКФ); |
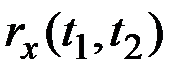
| – | нормированная ВКФ процессов X(t) и Y(t); |
| Sx(w) | – | спектральная плотность процесса X(t); |
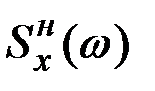
| – | нормированная спектральная плотность X(t); |
| w | – | круговая частота колебаний, рад/с; |
| f | – | циклическая частота колебаний, обратная величина единицы времени |
1. СЛУЧАЙНЫЕ СОБЫТИЯ
1.1. Элементарные понятия случайных событий
Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях.
Случайное явление – это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз по иному. Случайное явление на практике часто проявляется в виде случайных событий, случайных величин, случайных процессов.
Случайное событие – это всякий факт, который в результате опыта может произойти или не произойти.
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее, какое именно.
Случайным процессом (или случайной функцией) называется процесс, который в результате опыта может принять тот или иной конкретный вид, причём заранее неизвестно, какой именно.
Для количественного сравнения случайных событий между собой по степени их возможности используют понятие вероятности события.
Вероятность 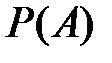 случайного события
случайного события 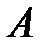 – это численная мера степени объективной возможности наступления этого события.
– это численная мера степени объективной возможности наступления этого события.
Достоверным называется событие, которое в результате опыта непременно должно произойти. Здесь 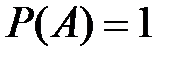 .
.
Невозможным называется событие, которое в результате опыта не может произойти: 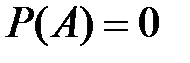 .
.
Вероятность события 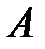 заключается между нулём и единицей:
заключается между нулём и единицей:
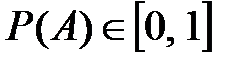 .
.
Несколько событий в данном опыте образуют полную группу, если в результате опыта должно появиться хотя бы одно из них.
Несколько событий называются несовместными в данном опыте, если никакие два из них не могут появиться вместе.
Несколько событий называются в данном опыте равновозможными, если объективная возможность их появления одинакова.
Если события в данном опыте несовместны, равновозможны и образуют полную группу, то они называются случаями или шансами. При этом вероятность события 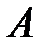 равна отношению числа m случаев, благоприятствующих появлению этого события, к общему числу случаев n:
равна отношению числа m случаев, благоприятствующих появлению этого события, к общему числу случаев n:
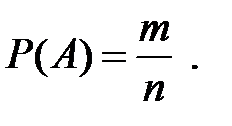
Эта формула работает при дискретном количестве случаев.
При решении геометрических задач вероятность того или иного события определяется отношением геометрического размера (длины, площади, объёма, угла и т.п.), благоприятствующего появлению рассматриваемого события (m), к общему размеру (n).
Непосредственный расчёт вероятности по указанной выше формуле в случае симметрии возможных исходов часто включает элементы комбинаторики.
Размещением из n элементов по m называется упорядоченная выборка элементов. Если среди n элементов все различные, то число размещений из n элементов по m определяется соотношением:
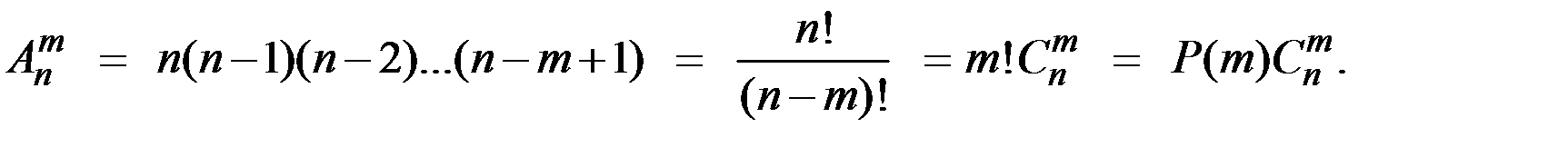
Размещениями с повторениями называют упорядоченные последовательности, составленные из n элементов по m, где некоторые из элементов (или все) могут оказаться одинаковыми. Число размещений с повторениями из n элементов по m определяется соотношением
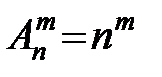 .
.
При m = n размещения называются перестановками, т.е. различные перестановки отличаются только порядком элементов.
Число перестановок из n элементов определяется формулой
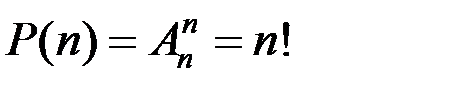
Сочетанием из n элементов по m называется выборка m элементов без учёта их порядка, т.е. различные выборки отличаются самими элементами. Если среди n элементов все различные, то число сочетаний определяется соотношением
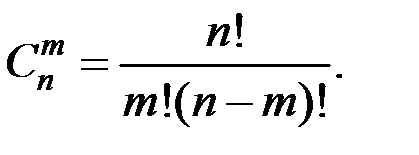
Отметим, что 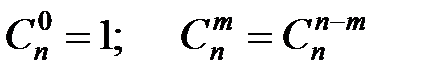 .
.
Последним свойством удобно пользоваться, когда 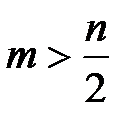 .
.
Количество различных способов разбиения n элементов на m групп с числом 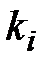 элементов в
элементов в 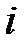 –й группе (перестановки с повторениями) определяется по формуле
–й группе (перестановки с повторениями) определяется по формуле
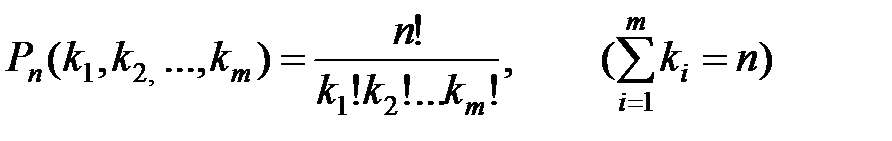 .
.
Пусть n–элементное множество 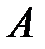 является суммой множеств
является суммой множеств 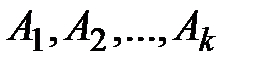 , число элементов которых равно соответственно
, число элементов которых равно соответственно 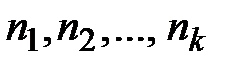 ,
, 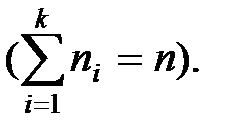 И пусть
И пусть 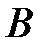 – m–элементное подмножество множества
– m–элементное подмножество множества 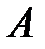 , содержащее
, содержащее 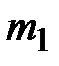 элементов из
элементов из 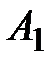 ,
, 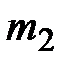 элементов из
элементов из 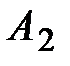 , ...,
, ..., 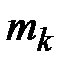 элементов из
элементов из 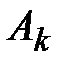
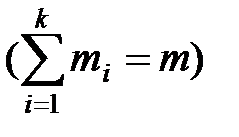 . Число способов, которыми можно выбрать такое множество В из А (множества неупорядоченные), равно
. Число способов, которыми можно выбрать такое множество В из А (множества неупорядоченные), равно 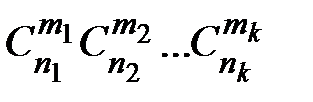 .
.
Пример 1.1. В ящике a белых и 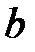 черных шаров
черных шаров 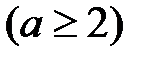 . Из ящика вынимают сразу два шара. Найти вероятность того, что оба шара будут белыми. Вычислить эту вероятность при a = 10,
. Из ящика вынимают сразу два шара. Найти вероятность того, что оба шара будут белыми. Вычислить эту вероятность при a = 10, 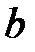 = 8.
= 8.
Решение. Общее число случаев взятия двух шаров
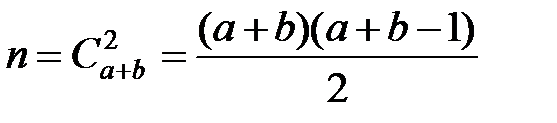 .
.
Число благоприятных случаев (когда оба шара белые)
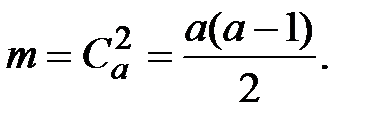
Тогда вероятность искомого события
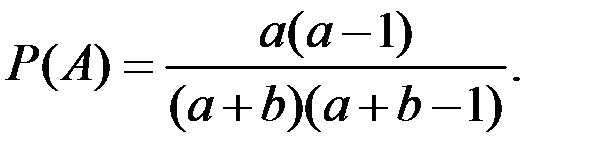
Вероятность искомого события при a = 10, 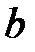 = 8:
= 8:
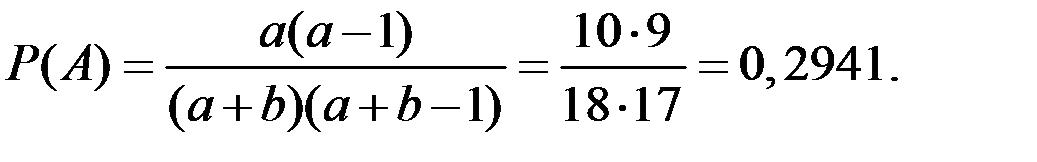
Пример 1.2. Игральная кость бросается один раз. Найти вероятность следующих событий: 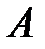 – появление чётного числа очков,
– появление чётного числа очков, 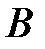 – появление не менее 5 очков,
– появление не менее 5 очков,  – появление не более 5 очков.
– появление не более 5 очков.
Решение. Определяем отношение числа благоприятных случаев к их общему числу:
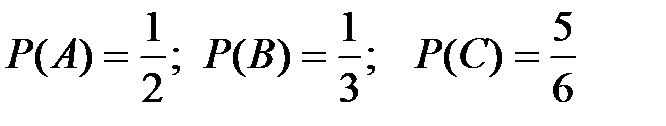 .
.
Пример 1.3. Найти вероятность того, что сумма двух случайных чисел из отрезка [0; 1] не превосходит единицы, а их произведение не меньше 0,09.
Решение. Найдём геометрическое место точек в квадрате со сторонами 1, где указанные условия выполняются.
Имеем границу области 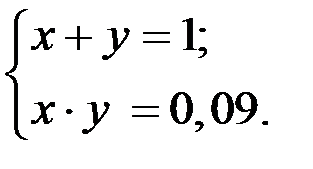
Точки пересечения можно найти, решив эту систему уравнений.
В результате получим 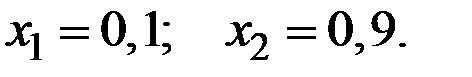
Тогда искомая вероятность равняется площади фигуры, ограниченной линиями 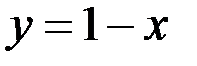 и
и 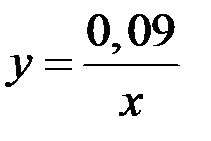 , и определяется следующим образом
, и определяется следующим образом
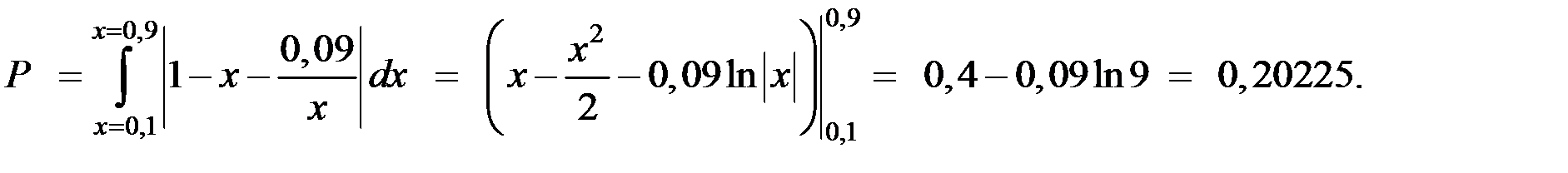
Пример 1.4. Шар радиуса R движется на забор из штакетника, расстояние между которыми равно а. Найти вероятность того что шар проскочит забор, не зацепив штакетника, если толщиной штакетника пренебречь.
Решение. Используем понятие геометрической вероятности:
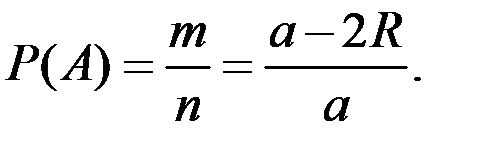
Пример 1.5. Какова вероятность того, что при игре в преферанс в прикупе окажутся 2 туза?
Решение. Используем формулу непосредственного вычисления вероятности события с использованием элементов комбинаторики:
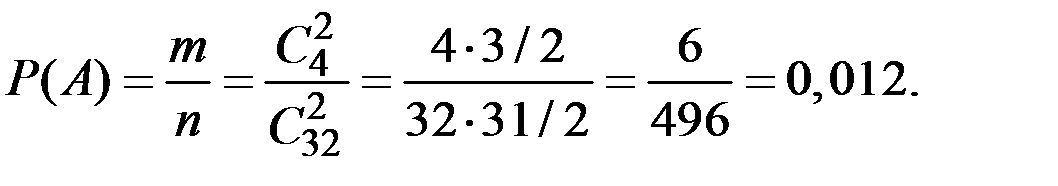
Пример 1.6. Кусок проволоки длиной 20 см был согнут в точке, выбранной наугад (точка сгиба равномерно распределена). После этого, перегнув ещё в двух местах, сделали прямоугольную рамку. Найти вероятность того, что площадь полученной рамки не превосходит 21 кв. см.
Решение. Пусть x – есть расстояние от точки первого сгиба до ближайшего конца, тогда площадь прямоугольника S = x Ч(10 – x).
Из условия
x Ч(10 – x) Ј 21
находим, что либо x О (0; 3), либо x О (7; 10).
Поэтому нужная рамка получится, если точка сгиба попадает в один из промежутков (0; 3), (7; 13), (17; 20) по длине стержня.
Искомая вероятность определится отношением благоприятствующей событию длины проволоки (m = (3 – 0) + (13 – 7) + (20 – 17) = 12) к общей длине (n = 20):
P = m/n = 0,6.
1.2. Аксиоматический подход в теории вероятностей
Логическим фундаментом всей современной теории вероятностей служит аксиоматическое определение вероятности.
В каждой вероятностной задаче задаётся некоторое непустое множество 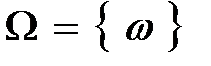 , элементы (или точки) которого интерпретируются как взаимоисключающие исходы изучаемого случайного явления.
, элементы (или точки) которого интерпретируются как взаимоисключающие исходы изучаемого случайного явления.
Определяется некоторая система a подмножеств множества  , называемых случайными событиями.
, называемых случайными событиями.
Любое случайное событие отождествляется с некоторым подмножеством 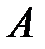 множества
множества  и интерпретируется как попадание элементов события
и интерпретируется как попадание элементов события 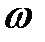 в множество
в множество 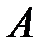 .
.
Для каждого случайного события 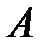 определяется числовая функция
определяется числовая функция 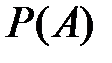 , называемая вероятностью события
, называемая вероятностью события 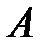 .
.
Множество a событий А 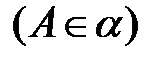 должно быть
должно быть 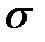 – алгеброй.
– алгеброй.
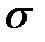 –алгеброй называется непустая совокупность подмножеств
–алгеброй называется непустая совокупность подмножеств 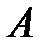 некоторого множества со следующими свойствами:
некоторого множества со следующими свойствами:
1) 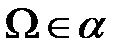 ;
;
2) если 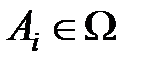 ,
, 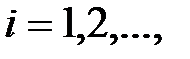 то
то 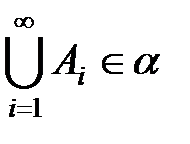 ;
;
3) если 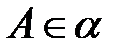 ,
, 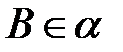 , то
, то 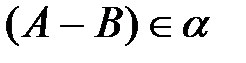 ;
;
4) если 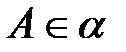 ,
, 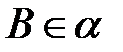 , то
, то 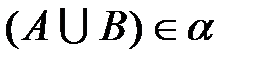 ;
;
5) если 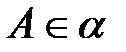 ,
, 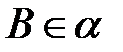 , то
, то 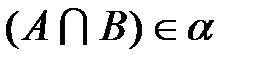 ;
;
6) если 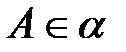 , то
, то 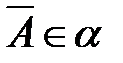 .
.
Проще говоря, 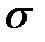 –алгебра a обладает тем свойством, что операции пересечения
–алгебра a обладает тем свойством, что операции пересечения 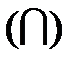 , вычитания (-), объединения
, вычитания (-), объединения 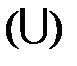 , дополнения (-), производимые над множествами из a, не выходят за её пределы, а операцию объединения можно при этом производить бесконечное (счётное) число раз.
, дополнения (-), производимые над множествами из a, не выходят за её пределы, а операцию объединения можно при этом производить бесконечное (счётное) число раз.
Вероятность 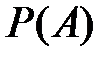 определяется для всех
определяется для всех 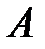 некоторой
некоторой 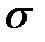 –алгебры из a.
–алгебры из a.
Для функции 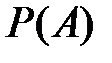 должны быть выполнимы следующие аксиомы:
должны быть выполнимы следующие аксиомы:
1) 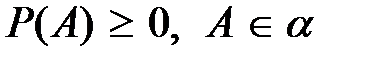 ;
;
2) 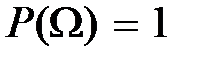 ;
;
3) аксиома счётной аддитивности (расширенная аксиома сложения): если 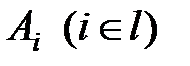 – непересекающиеся множества, где l – конечное или счётное множество, то
– непересекающиеся множества, где l – конечное или счётное множество, то 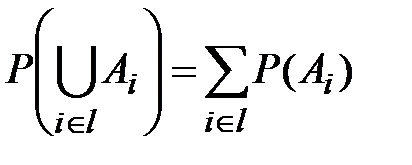 ;
;
4) аксиома полноты: функция 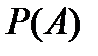 определена для любых подмножеств множества нулевой вероятности, т.е. если для
определена для любых подмножеств множества нулевой вероятности, т.е. если для 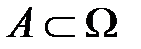 определена
определена 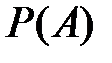 , причём
, причём 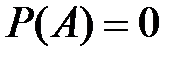 , а B – любое множество, входящее в A (хотя, возможно, и не принадлежащее a), тогда
, а B – любое множество, входящее в A (хотя, возможно, и не принадлежащее a), тогда 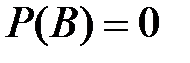 .
.
Тройка ( 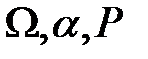 ), где
), где  – произвольное множество, a – s–алгебра подмножеств
– произвольное множество, a – s–алгебра подмножеств  ,
, 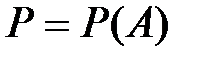 – вероятность, определённая на a и удовлетворяющая перечисленным выше условиям, называется вероятностным пространством.
– вероятность, определённая на a и удовлетворяющая перечисленным выше условиям, называется вероятностным пространством.
Функция 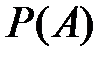 называется также вероятностной мерой, нормированной условием
называется также вероятностной мерой, нормированной условием 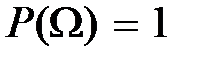 .
.
Из приведённых выше аксиом выводятся следующие основные соотношения между вероятностями событий:
1) 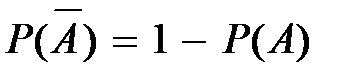 ;
;
2) если 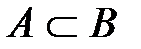 , то
, то 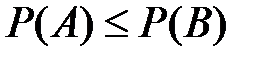 ;
;
3) 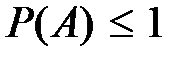 ;
;
4) пусть 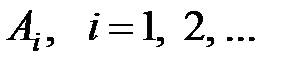 любое множество из a. Образуем множество
любое множество из a. Образуем множество
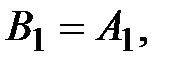
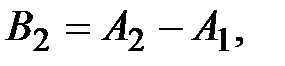
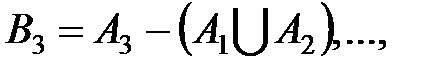
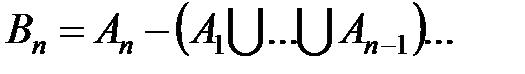
Тогда 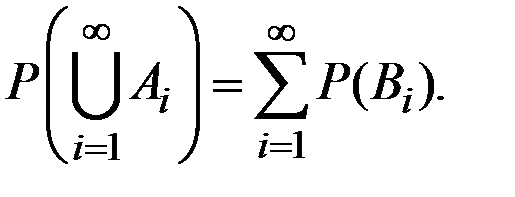
Пусть  множество в n–мерном евклидовом пространстве, объём (или мера)
множество в n–мерном евклидовом пространстве, объём (или мера) 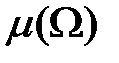 которого положителен и конечен.
которого положителен и конечен. 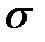 –алгебра a здесь состоит из всех измеримых (т.е. имеющих объем) подмножеств
–алгебра a здесь состоит из всех измеримых (т.е. имеющих объем) подмножеств 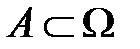 .
.
Тогда вероятность 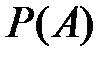 определяется равенством
определяется равенством
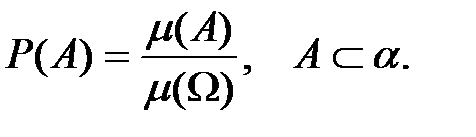
Такое определение вероятности называют геометрическим определением вероятности.
Пример 1.7. Найти вероятность того, что сумма выпавших очков на двух игральных кубиках делится на 6.
Решение. Исход опыта можно описать парой чисел 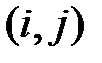 , где
, где 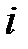 – число очков, выпавших на 1–м кубике, а
– число очков, выпавших на 1–м кубике, а  – на 2–м
– на 2–м 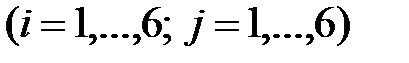 .
.
Поэтому 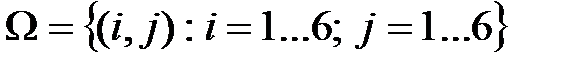 .
.
Общее число элементарных событий 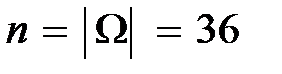 .
.
Интересующее нас событие 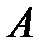 соответствует подмножеству
соответствует подмножеству 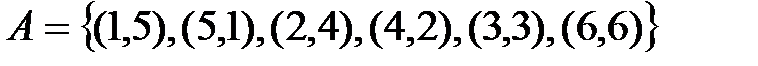 множества
множества  .
.
Так как 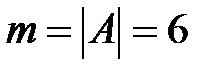 (число элементов множества
(число элементов множества 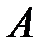 ), то искомая вероятность
), то искомая вероятность
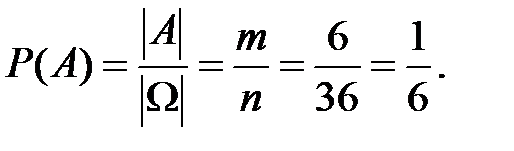
Пример 1.8. Два студента договорились зайти на кафедру на "большой" перемене (например, между 11–15 и 12–00). Каждый ждёт другого 10 минут, а потом уходит. Найти вероятность того, что студенты встретятся.
Решение. Множеством элементарных событий здесь является множество 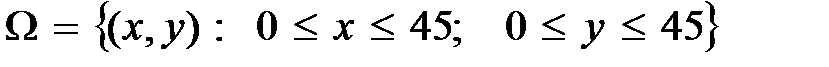 , где
, где 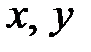 – моменты прихода студентов на кафедру относительно начала отсчёта времени (рис. 1.1).
– моменты прихода студентов на кафедру относительно начала отсчёта времени (рис. 1.1).
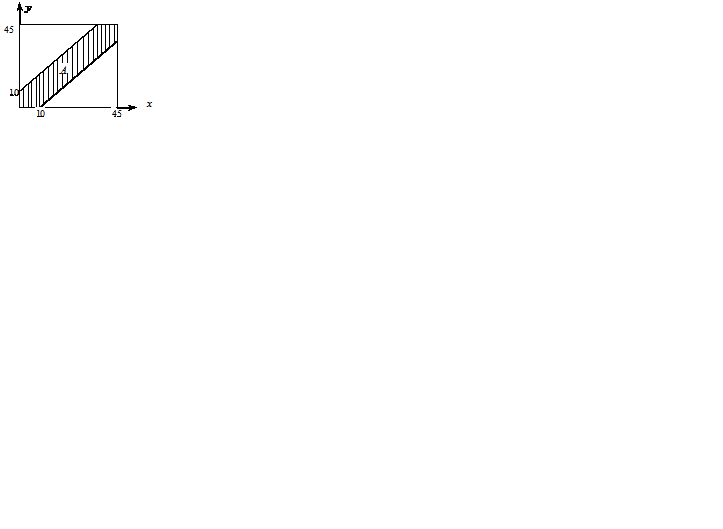
Рис. 1.1. Геометрическая интерпретация задачи о встрече
Тогда событие 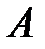 = {встреча студентов происходит} соответствует множеству
= {встреча студентов происходит} соответствует множеству 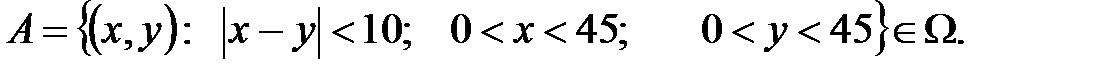
Так как 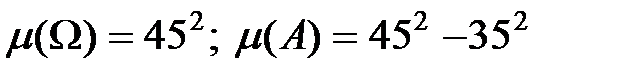 , то
, то
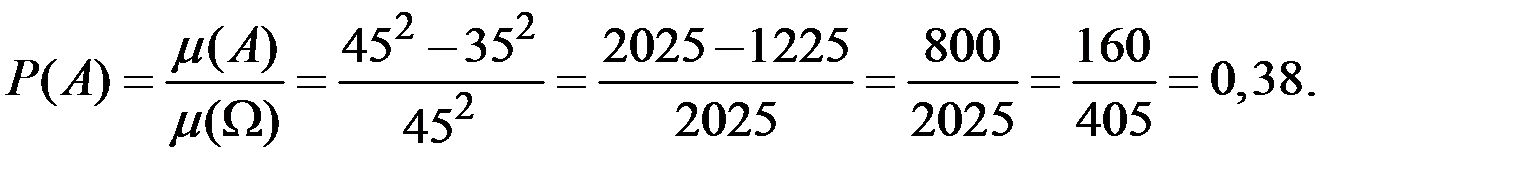
Если большая перемена длится 30 минут (с 13–10 до 13–40) то вероятность встречи студентов: