Сравнение ортогональных и линейно независимых сигналов
Применение ортогональных переносчиков для организации многоканальной передачи сообщений, с одной стороны, существенно упрощает процедуру разделения группового сигнала на приеме, а с другой стороны, обеспечивает большую в сравнении с линейно независимыми переносчиками помехозащищенность сигнала на приеме. Покажем это на примере.
Пример: Предположим, что необходимо передать два независимых сигнала ac(t) и аs(t) методом ФРK. Тогда групповой сигнал S ( t ) примет вид
,
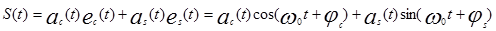где ec ( t ), es ( t )- линейно независимые переносчики; φc, φs - фазовые сдвиги соответственно сигналов ac ( t ) и а s ( t ). Для выделения из S ( t ) исходных первичных сигналов ac(t), as(t) на приемной стороне необходимо применить взаимно ортогональные базисные функции
,
.
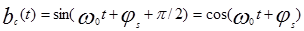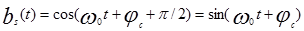Здесь bc ( t ) ортогонален es(t), а bc(t) ортогонален ec(t).
Применив к групповому сигналу операторы разделения, соответственно получим
,
.
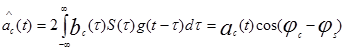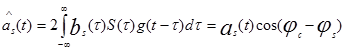Из приведенных соотношений следует, что оценки переданных первичных сигналов будут максимальны, когда φс-φs=0, т. е. когда переносчики ec(t), es(t) взаимно ортогональны.
Групповой сигнал S(t),сформированный на передаче даже с применением ортогональных переносчиков,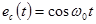 
и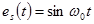 
, проходя по направляющей среде, подвергается воздействию различных искажений, например может возникнуть фазовый сдвиг φ каждого из несущих колебаний канальных сигналов Sc(t), Ss(t). В результате этого принимаемый сигнал будет иметь вид:
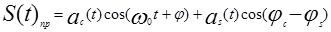
Если на приемной стороне при разделении применяются базисные функции ec(t), es(t), то оценки переданных первичных сигналов соответственно будут в виде
,
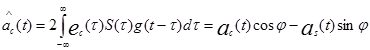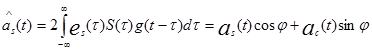
Из этих соотношений видно, что отсутствие ортогональности между первичными сигналами и базисными функциями на приеме уменьшает мощность выделенных первичных сигналов на cos φn. Кроме того, появляются переходные влияния между каналами, т.е. на выходе синфазного канала помимо основного сигнала ac(t)cosφ появляется сигнал as(t)cosφ. Аналогичное явление имеет место и в квадратурном канале.
1.5. ПОСТРОЕНИЕ КАНАЛОВ ДВУСТОРОННЕГО ДЕЙСТВИЯ