Метод временного разделения каналов
Основой построения метода временного разделения каналов (ВРК) является теорема Котельникова, в соответствии с которой непрерывный на интервале {-∞‚∞} первичный сигнал a ( t ) с граничной частотой спектра fmax может быть представлен в форме ряда так называемых отсчетных базисных функций g(t)i или
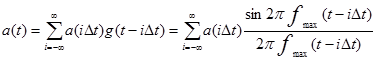
| (1.19) |
где a ( iΔt) - отсчеты непрерывного сигнала a ( t ), взятые в моменты времени iΔt; 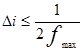 - интервал дискретизации непрерывного сигнала a ( t ).
- интервал дискретизации непрерывного сигнала a ( t ).
Базисные функции gi(t), gj(t) ортогональны на бесконечно большом интервале времени, т.е. для них справедливо
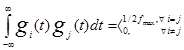
Как следует из (1.19), все сведения о передаваемом первичном сигнале a ( t ) содержатся только в отсчетах a ( iΔt ), а базисные функции gi ( t ) для всех I одинаковы по форме и отличаются друг от друга сдвигом во времени. Поэтому вместо непрерывного сигнала a ( t ) можно передавать лишь последовательность отсчетов
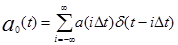
| (1.20) |
где δ(t)-дельта-функция, а базисные функции gi(t) восстанавливать на приеме.
Из сравнения (1.19) и (1.20) легко заметить, что (1.19) является результатом свертки во времени последовательности отсчетов a0(t) с одной базисной функцией g(t)=(sin2πfmaxt)/(2πfmaxt), являющейся импульсной характеристикой идеального ФНЧ с полосой пропускания 0…fmax
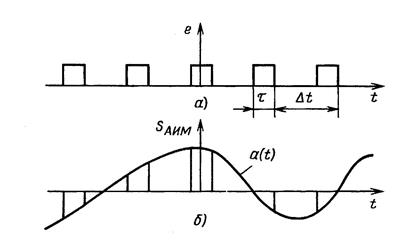
Рис. 1.17 - Формирование сигналов с АИМ
Поскольку сформировать последовательность отсчетов практически невозможно, то обычно первичный сигнал a ( t ) умножают на периодическую последовательность прямоугольных импульсов конечной длительности (рис. 1.17). В этом случае импульсную последовательность следует считать переносчиком или импульсной несущей, а сам модулированный сигнал S ( t )= a ( t ) e ( t ) тогда следует называть сигналом амплитудно-импульсной модуляции (АИМ)
Импульсную несущую e ( t ) можно представить в виде ряда Фурье:
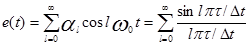 ,
,
где 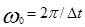 - круговая частота дискретизации;τ- длительность импульсов; αl-коэффициенты ряда Фурье.
- круговая частота дискретизации;τ- длительность импульсов; αl-коэффициенты ряда Фурье.
С учетом этого АИМ сигнал принимает вид
S(t)АИМ= 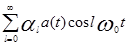
В последнем соотношении каждое из слагаемых определяет АМ колебание с ДБП частот около каждой гармоники импульсной несущей.
Поэтому спектр АИМ сигнала будет определяться в виде (рис. 1.18)
S(ω)АИМ= 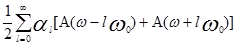 .
.
Слагаемое с l =0 соответствует исходному первичному сигналу и может быть выделено из спектра S(ω)АИМ c помощью ФНЧ при условии, что ω0 ≥2Δω.
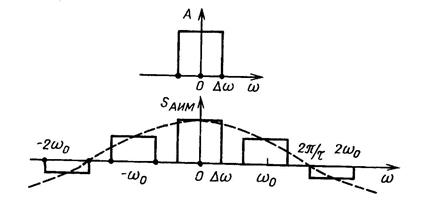
Рис. 1.18 - Спектр сигналов с АИМ
При организации многоканальной передачи сообщений каждому первичному сигналу an ( t ) ставится в соответствие переносчик
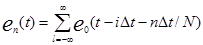 ,
,
где е0( t )- единичный импульс в импульсной несущей.
Тогда групповой сигнал МСП с ВРК и АИМ будет определяться в виде
S(t) ВРК АИМ = 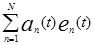 ,
,
а алгоритм разделения аналогичен ранее рассмотренным алгоритмам, т. е.
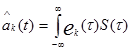 ВРК АИМ ВРК АИМ 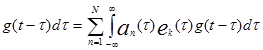
| (1.21) |
В (1.21) все интегралы, (кроме случая, когда п= k) равны нулю, поскольку переносчики en ( τ ), ek ( τ ) ортогональны с весом g(t+ τ) на бесконечном интервале времени. Единственный ненулевой интеграл определяет отклик ФНЧ на входной сигнал Sk(t) АИМ, который равен 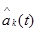
Сигналы АИМ применяются во всех МСП с ВРК, в частности в ЦСП с ИКМ.
На рис. 1.19 приведены временные диаграммы переносчиков разных каналов, с помощью которых осуществляется процесс формирования группового сигнала ВРК АИМ. Структурная схема МСП с ВРК АИМ представлена на рис.1.20.
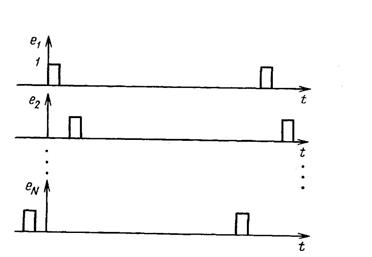
Рис. 1.19 - Ортогональные переносчики системы передачи с ВРК АИМ
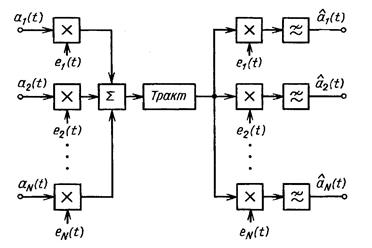
Рис.1 20 - Структурная схема системы передачи с ВРК АИМ
Сопоставление рассмотренных алгоритмов показывает, что все существующие МСП с ЧРК ДБП, ФРК,ЧРК ОБП и ВРК АИМ строятся согласно одному общему правилу. На передаче в процессе формирования группового сигнала осуществляется сложение первичных сигналов an ( t ) ,умноженных на базисные функции -переносчики en ( t ). Разделение группового сигнала на приеме выполняется путем вычисления скалярного произведения группового сигнала S(t) и ek(t) с весовой функцией g ( t ), являющейся импульсной характеристикой ФНЧ.








