Многоканальная передача сигналов с разделением по фазе
При фазовом разделении сигналов (ФРС) для каждого номинала несущей частоты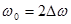 
нужно использовать переносчики вида
,
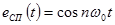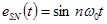
Тогда групповой двухканальный сигнал для n-й несущей частоты можно представить так
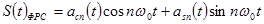
| (1.15) |
Разделение двухканального сигнала на приеме необходимо и здесь осуществить путем вычисления скалярного произведения группового сигнала и векторов- переносчиков, т.е. согласно алгоритму
,
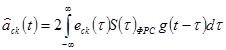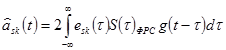
Структурная схема МСП, реализующая метод ФРК для одной несущей, приведена на рис. 1.11.
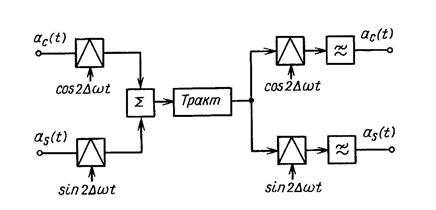
Рис.1.11 - Структурная схема системы передачи с ФРК
Следует обратить внимание, что при ФРК на каждой несущей частоте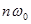 
обеспечивает передача двух независимых первичных сигналов 
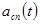и 
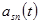в полосе частот 
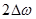. Следовательно, при одинаковом числе каналов (N-четном) МСП с ФРК требует в сравнении МСП с ЧРК ДБП в 2 раза меньшую полосу частот. Это обеспечивается тем, что при одной и той же частоте несущего колебания 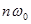первичные сигналы 
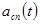и 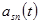передаются с помощью ортогональных переносчиков
,
.
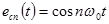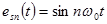Ортогональность переносчиков обеспечивается за счет фазового сдвига на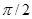 
между ними. Соответственно и все спектральные составляющие канальных сигналов 
, 
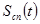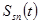будут сдвинуты друг относительно друга на угол 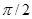(рис.1.12).
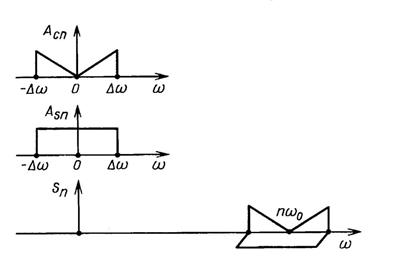
Рис. 1.12 - Формирование спектра системы с передачи с ФРК
Многоканальная передача сигналов амплитудной модуляции с одной боковой полосой частот
Свойство четной симметрии спектра сигнала АМ относительно частоты несущего колебания говорит о том, что в обеих боковых полосах частот содержится одинаковое количество информации о передаваемом сообщении. Поэтому достаточно передавать Ам сигнал только с одной боковой полосой (ОБП) частот. При этом ширина полосы частот группового сигнала будет в два раза меньше, чем при АМ – ДБП.
Рассмотрим механизм формирования сигнал АМ ОБП рис. 1.13 представив его спектр в виде суммы двух спектров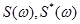 
:
.
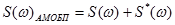Если первичному сигналу a(t) соответствует спектр A(w), то АМ колебанию S(t) с двумя боковыми полосами частот соответствует спектр
.
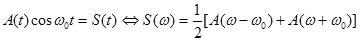Как следует из рис.1.2, ненужная боковая полоса частот АМ ОБП колебания компенсируется с помощью сигнала, которому соответствует спектр S*(w). Найдем структуру компенсирующего сигнала S*(w), выполнив преобразования Фурье над S*(w).
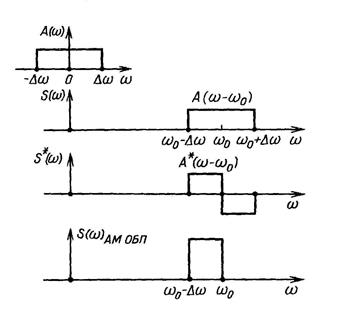
Рис.1.13 - Формирование спектра сигнала АМ ОБП колебания
Поскольку спектр действительных сигналов всегда является четной функцией частоты, то следует применять cos-преобразование Фурье, в соответствии с которым
 =  .
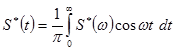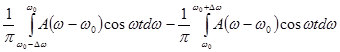| (1.16) |
Сделав замену переменной интегрирования в приведенной формуле и обозначив W=w-w0, после несложных преобразований приходим к результату
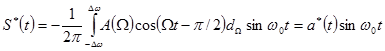
где а*(t)- первичный сигнал, преобразованный по Гильберту.
Следовательно,
.
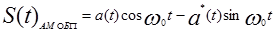Таким образом, АМ колебание с ОБП частот состоит из двух АМ колебаний с ДБГ. При этом вся информация о передаваемом сообщении содержится в первом АМ колебании, в то время как второе слагаемое выполняет роль, компенсирующего сигнала для подавления ненужной боковой полосы частот.
Структурная схема формирователя АМ ОБП колебания приведена на рис. 1.14.
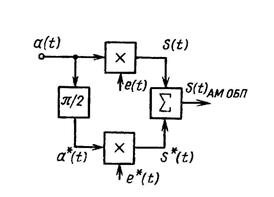
Рис. 1.14 - Структурная схема формирователя АМ ОБП колебания
Поскольку ширина спектра АМ ОБП колебания равна Dw, то и разность между соседними несущими частотами должна (может) быть равной w0=Dw. Тогда групповой сигнал МСП с ЧРК ОБП будет определяться суммой
S(t)ЧРК ОБП=  .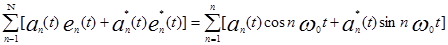
| 1.17 |
Спектральные диаграммы, поясняющие процесс формирования группового сигнала МСП с ЧРК ОБП, приведены на рис. 1.15.
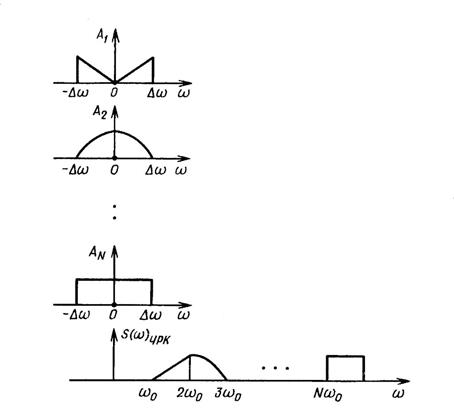
Рис.1.15. - Формирование спектра группового сигнала системы передачи с ОБП
Процесс разделения группового сигнала при ЧРК ОБП сводится к вычислению двух скалярных произведений с последующим суммированием их результатов, т. е.
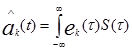ЧРКОБП 
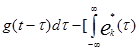ЧРКОБП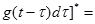 
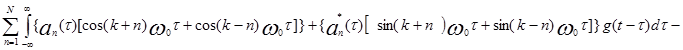
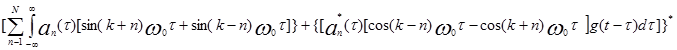
Все слагаемые, соответствующие суммарным частотам первой суммы, будут равны нулю, поскольку они определяют АМ колебания, спектры которых находятся вне полосы пропускания ФНЧ. Из разностных продуктов ненулевыми будут только слагаемые с n=k, n=k+1. Аналогичные ненулевые продукты будут и для второй суммы.
После преобразования по Гильберту ненулевых продуктов второй группы слагаемых и их суммирования с первыми слагаемыми оказывается, что все побочные продукты компенсируются, а остается лишь оценка полезного первичного сигнала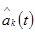 
. Для большей наглядности приведем простой пример.
Пример. Пусть первичные сигналы составляют совокупность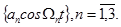 
Тогда групповой трехканальный сигнал будет определяться суммой
.
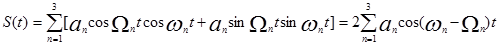Как следует из этого соотношения, групповой сигнал состоит только из нижних боковых полос АМ колебаний.
Теперь пусть на приеме необходимо выделить первичный сигнал с k=2. Скалярное произведение группового сигнал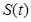 
с 
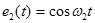дает
.
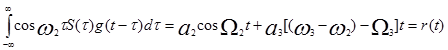После вычисления скалярного произведения группового сигнала 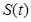с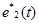 
и последующего преобразования результатов по Гильберту получаем
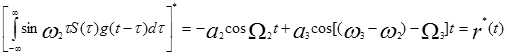
Объединяя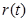 
с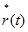 
,с учетом знака находим, что
.
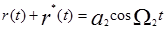На практике в большинстве случаев одна боковая полоса частот АМ колебания выделяется с помощью полосового фильтра (ПФ).
На рис. 1.16 приведена структурная схема МСП с ЧРК ОБП, соответствующая алгоритмам (1.17), (1.18). На этой структурной схеме выделение одной боковой полосы частот осуществляется с помощью ПФ.
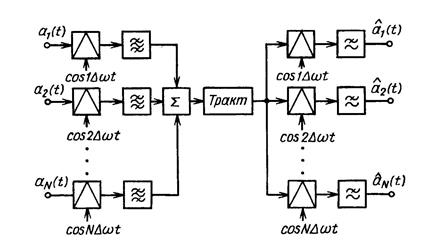
Рис. 1.16 - Структурная схема системы передачи с ОБП