Разделение сигнала с конечной мощностью
Рассмотренные до сих пор методы организации многоканальной передачи применимы к передачи дискретных во времени первичных сигналов или же отсчетов непрерывных сигналов. Вместе с тем идея использования для многоканальной передачи линейно независимых или ортогональных переносчиков может использоваться и для передачи непрерывных во времени первичных сигналов с ограниченным спектром. Однако здесь следует употреблять функции – переносчики ортогональные или хотя бы линейно независимые на бесконечном промежутке времени. Указанные свойства обеспечиваются за счет введения понятия ортогональности базисных функций с определенным весом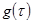 
, т.е.
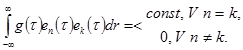
Для тригонометрических функций кратных аргументов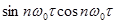 
, а также для периодических последовательностей импульсов в качестве весовой функции следует применить импульсную характеристику ФНЧ. Например, импульсной характеристики вида (рис.1.8,а)
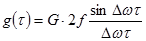
соответствует передаточная функция идеального ФНЧ (рис.1.8, б)
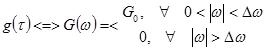
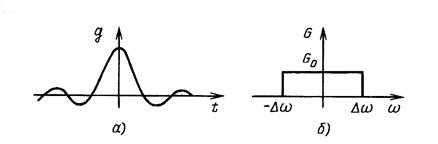
Рис. 1.8 – Импульсная характеристика идеального ФНЧ
Формирование групового сигнала при передаче непрерывных во времени первичных сигналов осуществляется согласно правилу
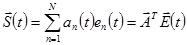
| (1.11) |
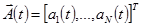-вектор первичных сигналов;
Алгоритм разделения группового сигнала в этом случае имеет вид
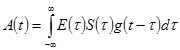
| (1.12) |
или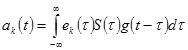 
, 
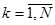
Приведенный алгоритм формирования группового сигнала (1.11) и алгоритм разделения (1.12) справедливы для всех типов МСП.
Многоканальная передача сигналов амплитудной модуляции с двумя боковыми полосами частот
Предположим, что все первичные сигналы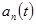 
имеют ограниченную ширину 
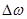спектра - 
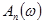. Тогда формирование группового сигнала амплитудной модуляции (АМ) с передачей двух боковых полос (ДБП) осуществляется в соответствии с (1.11), т.е.
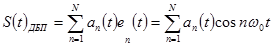
| (1.13) |
где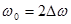 
.
Поскольку операции умножения функции 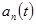во временной области и 
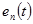в частной области соответствует свертка спектров сомножителей, то
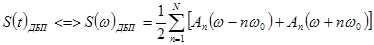
На рис. 1.9 приведены спектральные диаграммы первичных и группового сигналов, соответствующие передаче ДБП.
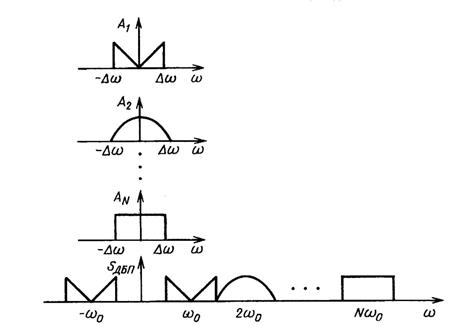
Рис. 1.9 - Формирование спектра группового сигнала системы передачи с ДБП
Разделение группового сигнала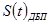 
на приеме необходимо делать согласно алгоритму
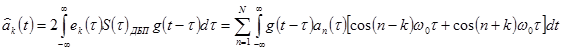
| (1.14) |
Из (1.14) видно, что все N интегралов определяют отклики ФНЧ с граничной частотой полосы пропускания 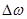на АМ колебания. Спектры всех колебаний в сумме, кроме слагаемого с n=k, расположены за полосой пропускания ФНЧ. Поэтому N-1 колебаний не проходят на выход ФНЧ, т.е. N-1 интегралов в (1.14) равно нулю. Единственный ненулевой интеграл определяет реакцию ФНЧ на 
.
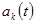Очевидно, что при G=1
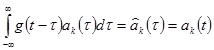
Структурная схема МСП с ДБП, соответствующая приведенным алгоритмам, представлена на рис 1.10.
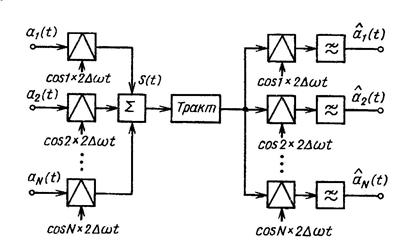
Рис. 1.10 - Структурная схема системы передачи ДБП