Разделение линейно независимых сигналов

Дата: 2025-06-02; Просмотры: 23

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Если переносчики не обладают свойством ортогональности, то разделение группового сигнала может быть выполнено но только согласно алгоритму (1.8), связанному с обращением матрицы Е. На приемной стороне формируется совокупность линейно независимых векторов 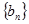, взаимно ортогональных к совокупности переносчиков .

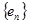При формировании векторов 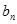нужно руководствоваться алгоритмом

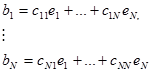
где коэффициент 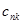определяется из N² линейных уравнений

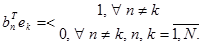
Пример. Пусть будут заданы два линейно независимых переносчика

; .

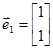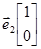Сформируем с помощью этих переносчиков групповой сигнал .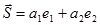

Для разделения этого группового сигнала на приеме образуем векторы 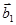и 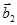взаимно ортогональные к 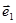и .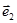

;

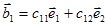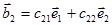
Вычислив коэффициенты 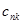из уравнений

; ; ; .

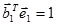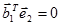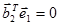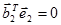Получим , .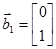

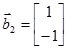Теперь выделение первичных сигналов a ₁ и a₂ из 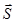сводится к операциям 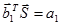и 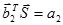соответственно.

Разделение сигналов с конечной энергией

Выделенные ранее понятия линейной независимости и ортагональности (ортонормированности) в полной мере справедливы и для непрерывных во времени переносчиков 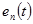, обладающих конечной энергии, т.е.

, .

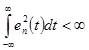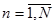Для таких переносчиков условие линейной независимости имеет место, когда тождество 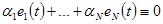правомерно только при условии .

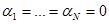Ортогональными (ортонормированными на интервале 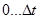) являются переносчики, для которых скалярные произведения удовлетворяют условиям

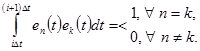
Такие переносчики, называемые иногда базисными функциями, широко применяются при организации многоканальной передачи дискретных сообщений. Алгоритм формирования группового сигнала на передачи с помощью таких переносчиков определяется аналогично (1.6), т.е.

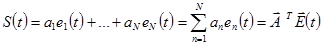
(1.9)

где 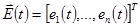- вектор переносчик: 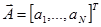- вектор первичных сигналов.

Процедура выделения первичных сигналов на приеме здесь так же определяется путем вычисления скалярных произведений, т.е.

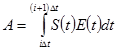
(1.10)

Поскольку переносчики по определению ортогональны на интервале 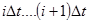, то векторный алгоритм разделения (1.10) разбиваются на N независимых скалярных алгоритмов:

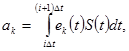
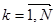
Свойством ортогональности обладает множество функций, например отрезки тригонометрических функций кратных аргументов, полиномы Чебышева, Лаггера, Эрмита, Лежандра, Уолша, Харра и др. На рисунке 1.7 приведена структурная схема МСП дискретных сигналов 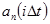с ортогональными базисными функциями .

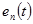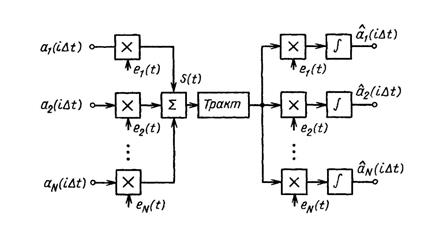
Рис. 1.7 - Структурная схема системы передачи с ортогональными переносчиками