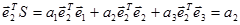Формировангие группового сигнала
С учетом введенных ранее обозначений перепишем систему линейных уравнений (1.2) в следующем виде:
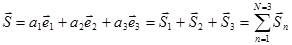
| (1.6) |
где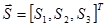 
- вектор группового сигнала.
Соотношение 1.6 является алгоритмом формирования группового сигнала. Векторы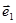 
, 
, 
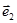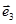принято называть переносчиками, а векторы 
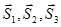- канальными сигналами.
Уравнение 1.6 можно представить более компактной форме
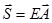
| (1.7) |
где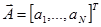 
- вектор первичных сигналов, матрица была определена ранее.
Очевидно решением данного уравнения относительно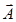 
является
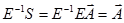
| (1.8) |
Это уравнение правомерно тогда, и только тогда, когда матрица Е неособенная, т.е. ее определитель не равен нулю, а это имеет место, когда переносчики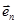 
линейно независимы. Таким образом, вновь убеждаемся, что линейная независимость переносчиков является необходимым и достаточным условием условием разделимости группового сигнала.
Ортогогнальные переносчики. Разделенние ортогональных сигналов
Как следует из (1,8), разделение группового сигнала на приеме сопряжено с обращением матрицы Е. При большей размерности этой матрицы, т.е. при большом N, операция обращения чрезвычайно трудоемка. Решение задачи существенно облегчается, если матрица ортогональна. Ортогональные матрицы обладают свойством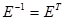 
.
Если матрица Е ортогональна, то должно выполнятся условие
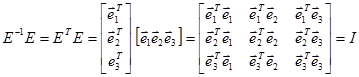
где I – единичная матрица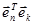 
скалярное произведение векторов 
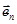и 
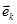соответственно.
Теперь видно, что для выполнения условия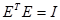 
необходимо одновременное выполнение следующих условий:
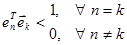
Из курса математики известно, что векторы, обладающие указанными свойствами, называются ортонормированными, т.е. ортогональными с единичной нормой (длинной) вектора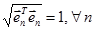 
. Свойство ортонормированности векторов – переносчиков обеспечивает разбиение векторного уравнения 
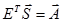на N не связанных скалярных уравнений:
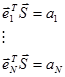или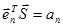 
, 
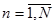
Таким образом, при применении ортогональных переносчиков операция разделения группового сигнала на приеме сводится к вычислению N скалярных произведений.
Пример. Пусть групповой сигнал будет сформирован из суммы ортогональных канальных сигналов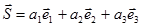 
/
Если требуется выделить на приеме первичный сигнал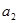 
, то это сводится к операции
