Условие линейного разделения сигналов

Дата: 2025-06-02; Просмотры: 17

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Условие линейной независимости уравнений системы (1.2), определяющее возможность линейного разделения группового сигнала на индивидуальные, означает, что столбцы матрицы Е, соответствующей определителю Δ , линейно независимы. Это же относится и к строкам. Условие линейной независимости столбцов соблюдается только тогда, когда тождество

,

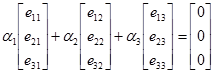(1.3)

что имеет место лишь при условии 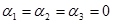. Если тождество выполняется хотя бы при одном 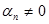, то система линейных уравнений (1.2) будет линейно зависимой, а следовательно, из группового сигнала {S₁, S₂, S₃} нельзя выделить первичные сигналы а₁, а₂, а₃.

В курсе линейной алгебры одностолбцовые матрицы принято называть векторами. Поэтому тождество (1.3) целесообразно переписать в виде

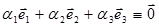
(1.4)

где 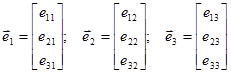-векторы

При выявлении связи между 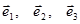следует составить определитель Грамс:

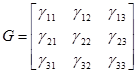, где 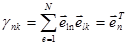, 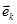-скалярное произведение векторов 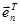и 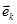; Т – означает знак транспонирования матрицы.

Транспонирование матрицы означает поворот ее относительно главной диагонали, а транспонирование вектора-столбца переводит в его вектор-строку. Например, если

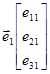, то .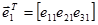

Если определитель Грама положителен, то векторы 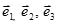линейно независимы. Если же G=0, то векторы будут линейно независимы.

Максимальное число линейно разделимых сигналов в N – мерном линейном пространстве

Размерность линейного векторного пространства определяется числом координат используемых векторов. Путь заданы, N линейно независимых векторов в N – мерном линейном пространстве. Тогда на основании (1.4) для этих векторов справедливо соотношение

.

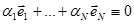(1.5)

Возьмем еще один вектор 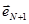в том же N - мерном пространстве. Добавив его в уравнение (1.5), получим

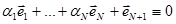
Это уравнение перепишем в виде

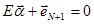
Где 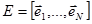- матрица, составленная из линейно независимых векторов, 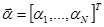- вектор коэффициентов .

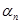Из этого уравнения находим, что 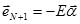или

.

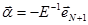Матрица Е не особенная, поскольку ее столбцы линейно независимы. Тогда если только 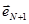не нулевой вектор, то и 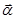не нулевой вектор. Поэтому вектор 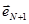является линейной комбинацией векторов 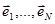. Следовательно, в N- мерном пространстве может быть лишь N линейно независимых сигналов

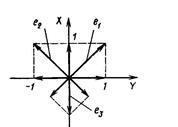
Рис.1.6 - К определению максимального числа линейно независимых сигналов

Например. Пусть будут заданы два вектора 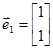; 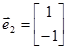. Возьмем третий вектор, например 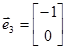. Составим уравнение 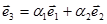. Решая это уравнение относительно 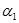, 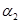определяем, что 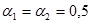. Таким образом, 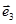линейно связан с 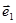и .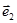

Поскольку векторы 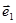и 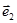представлены в двухмерном пространстве, т.е. на плоскости, то этот пример может быть легко решен геометрически. На рисунке 1.6 показаны векторы 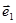и 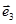; вектор 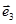определяется геометрической суммой векторов 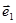и 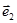.