Простейшие методы разделения сигналов
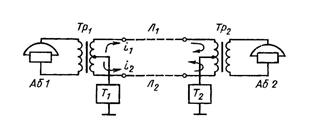
Простейшие методы организации многоканальной передачи сообщений основаны на применении двухпроводных линий связи с симметрирующими трансформаторами. Так, с помощью одной двухпроводной симметричной линии связи можно организовать одну несимметричную линию связи, называемую искусственной или фантомной цепью (рис.1.3). Несимметричная искусственная цепь была впервые предложена Пикаром для одновременной передачи телефонного и телеграфного сигналов.
Телефонная связь между абонентами Аб1 и Аб2 осуществляется по двухпроводной физической цепи. Абоненты к цепи подключены через дифференциальные трансформаторы Тр1 и Тр2. К средним точкам линейных обмоток трансформаторов подключены телеграфные аппараты Т1 и Т2, работающие по несимметричной искусственной цепи, одним проводом которой является земля. Ток i от телеграфного аппарата разветвляется: по проводу Л1 протекает ток i 1 , а по проводу Л2 – ток i 2 . При одинаковом сопротивлении этих проводов и симметрии их относительно земли i 1 = i 2 и создаваемые этими токами магнитные потоки в трансформаторах Тр1 и Тр2 компенсируют друг друга. Следовательно, явление телеграфного сигнала на телефонный отсутствует.
В настоящее время такой метод передачи используется только для организации дистанционного питания с обслуживаемых усилительных пунктов (ОУП) на необслуживаемые усилительные пункты (НУП), а также для передачи сигналов телеконтроля.
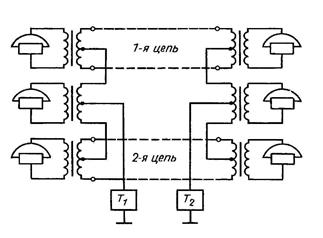
При наличии двух одинаковых двухпроводных цепей можно получить дополнительную искусственную двухпроводную цепь для организации телефонной связи и одну несимметричную искусственную цепь для передачи телеграфного сигнала (рис.1.4).
| 
|
| Рис1.3 - К понятию искусственной несимметричной цепи | Рис.1.4 - К понятию построения искусственной симметричной цепи |
Линейное разделение сигналов
Простейшие методы разделения сигналов имеют очень ограниченные возможности и всегда приводят к увеличению числа используемых физических цепей. В современных МСП групповой (многоканальный) сигнал передается по одной какой-либо среде распространения, т.е. по линии передачи - проводной, радиолинии, волноводно- или волоконно-оптической.
В процессе изучения основ теории разделения сигналов в первом приближении можно считать, что все первичные сигналы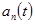 
имеют одинаковую природу, принадлежат одному пространству сигналов и обладают одинаковой шириной спектра 
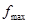. Поэтому на основании теоремы Котельникова каждый из первичных сигналов 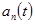полностью описывается отсчетами мгновенных значений 
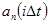, следующие через интервалы дискретизации 
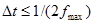. Следовательно, в конкретные моменты 
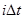отсчеты первичных сигналов проектируются в виде точек 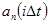на ось напряжений или токов (рис.1.5).
a 1 0 a 2 a 3 a
Рис. 1.5 - Пространство одномерных сигналов
В курсе МСП, ставится задача выделения из группового сигнала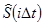 
всех первичных сигналов 
.
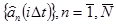Предположим, что на передающей стороне групповой сигнал формируется из совокупности первичных сигналов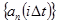 
путем их суммирования с определенными весовыми коэффициентами 
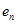, т.е.
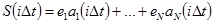
| (1.1) |
В каждый момент времени 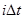конкретные значения 
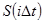передаются каким-либо образом из пункта передачи в приемный пункт. При отсутствии влияния помех и искажений в процессе передачи группового сигнала 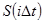в пункте приема он будет точно соответствовать переданному. Теперь, получив на приеме групповой сигнал и зная закон его формирования, а также полные сведения о коэффициентах 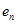, нужно найти 
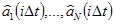, т.е. по существу ставится задача решения одного линейного уравнения с N неизвестными. Одно линейное уравнение с N неизвестными имеет бесчисленное множество решений, т.е., задача поставлена некорректно. Для того чтобы можно было бы выделить на приеме первичные сигналы из их сумм, необходимо произвести, по крайней мере, N измерений группового сигнала, т.е. получим N линейных уравнений.
Положим, например, N=3 и отступим для простоты аргумент дискретного времени в первичных и групповых сигналов. Тогда
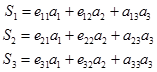
| (1.2) |
При наличии теперь на примере результатов трех измерений группового сигнала и априори известных коэффициентов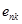 
систему линейных уравнений можно решить, например, методом Крамера, т.е. 
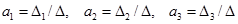, где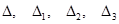 
-соответственно главный и вспомогательный определители.
Система линейных уравнений (1.2) обладает единственным решением, если главный определитель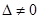 
. В противном случае система будет, либо несовместной, либо неоднозначной, т.е. иметь бесчисленное множество решений.
Условие 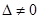означает, что линейные уравнения системы (1.2) независимы, т.е. ни одно уравнение этой системы не может быть получено путем линейной комбинации других уравнений.