Средняя мощность совпадает с дисперсией случайного процесса - мерой его разброса около среднего значения. Положительное значение называют эффективным или действующим напряжением сигнала.
Максимальная мощность Р max - это мощность синусоидального сигнала с амплитудой UM, которая превышается мгновенными значениями переменной составляющей сигнала u_(t) с определенной, достаточно малой вероятностью e. Для различных видов сигналов e принимают равной 10-2, 10-3 а иногда и 10-5 .
Минимальная мощность Р min - чаще всего принимается равной допустимой среднеквадратической ошибке при приеме сигналов данного вида, которая устанавливается экспериментально. В свою очередь, среднеквадратическая ошибка обычно равна средней мощности допустимой флуктуационной помехи: Р min = Рпер.
Иногда минимальная мощность сигнала принимается равной мощности синусоидального сигнала с амплитудой Uмmin, которая превышается мгновенными значениями переменной составляющей u_(t) с определенной, достаточно большой вероятностью (1-e). Обычно принимают (1 - e)=0.98.
Возможно использование логарифмических отношений выше названных величин:
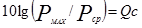- пик-фактор сигнала;
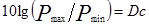- динамический диапазон сигнала;
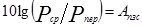- помехозащищенность сигнала.
Две последние величины используются и для характеристик трактов передачи сигналов. При этом:
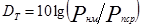, где Рнм- неискаженная мощность на выходе тракта,
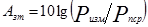, где Ризм- мощность измерительного сигнала на выходе.
Тогда при передаче сигналов должны выполняться следующие неравенства
.
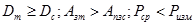Для оценки скорости изменения сигнала используют функцию автокорреляции
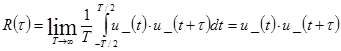
Очевидно, что при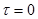 
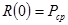. Величина 
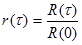называется коэффициентом автокорреляции. Собственно мерой скорости изменения сигнала является интервал корреляции t0 - время, через которое утрачивается статистическая зависимость между u_(t) и u_(t+t):
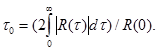
Посредством косинус - преобразования Фурье можно получить спектральную плотность процесса G(f) по функции автокорреляции:
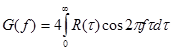
или обратно
,
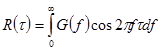где G(f) - спектральная плотность, или мощность процесса, определенная в бесконечно малой полосе df вблизи частоты f. В конечной полосе частот средняя мощность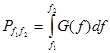 
.
Эффективная ширина энергетического спектра сигнала
,
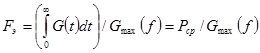где Gmax(f)- максимальное значение спектральной плотности. Очевидно, что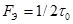 
.
Эффективную ширину энергетического спектра сигнала не следует смешивать с эффективно передаваемой полосой частот сигнала, которая устанавливается экспериментально исходя из необходимо высокого качества передачи.