Теория вероятностей.
1.1. Исторические сведения и основание
для возникновения теории вероятностей.
Теория вероятностей возникла в середине 17 века в связи с развитием азартных игр. У истоков развития стояли математики: Паскаль ( кавалер де Мере ), Ферми, Гюйгенс. Они первыми решили задачи о вероятности исхода в азартных играх с костями и картами, в которых реализовывались случайные события. Большое значение в становлении и развитии теории вероятностей сыграли работы математиков Якоба Бернули, Муавра, Лапласа, Гаусса, Пуассона, а также российских учёных Чебышева, Маркова, Лягупова и др.
1.2. Основные понятия ТВ. Непосредственный подсчет вероятностей.
Событием ( случайным событием ) называется всякий факт, который в результате опыта может произойти или не произойти.
В окружающем нас мире можно наблюдать событие (явление) следующих классов:
А) Достоверные события – такие события, которые при соблюдении определённых условий обязательно произойдут.
Б) Невозможные события – такие события, которые в результате опыта не могут произойти.
В) Случайные события – такие события, которые могут как произойти, так и не произойти при данных определённых условиях. Случайность событий, то есть принципиальная неопределённость исхода испытания связана с тем, что в ходе испытания с некоторым объектом на него воздействуют очень много внешних факторов, воздействие которых на данный объект учесть в принципе невозможно.
Обозначение событий: случайные события обозначают первыми буквами латинского алфавита (A, B, C, S), достоверные события – U, невозможные события –V. Вероятность события А обозначается Р(А).
Вероятность достоверного события равна 1:
Р(U) = 1.
Вероятность невозможного события равна 0:
Р(V) = 0.
Вероятность события А заключена между нулем и единицей:
0= < Р(А) =< 1.
Теория вероятностей, а также математическая статистика изучают не просто случайные явления, а случайные явления массового характера, вероятность наступления которого отлична от нуля. Если событие истинно случайное, но единичное или очень редкое, то оно не может быть предметом изучения теории вероятностей и статистики.
Например: студент спешил на лекцию, упал и сломал ногу. Событие случайное, но оно не является предметом изучения теории вероятностей, так как оно единично в жизни человека, вероятность близка к «0». Если студент опаздывает или не опаздывает на лекции при ежедневном их посещении, то опоздание носит не только случайный, но и массовый характер, то есть является предметом изучения теории вероятностей.
1.3. Основные понятия теории вероятностей.
1) Теория вероятностей – раздел математики, изучающий случайные явления и их закономерности.
2) Предмет теории вероятностей – случайные явления массового характера.
3) Цель теории вероятностей – вскрытие закономерностей, которым подчиняются случайные величины при условии их массового характера (во времени и пространстве).
4) Средства теории вероятностей: элементарная математика, опыты, геометрия, математический анализ, логика и комбинаторика.
5) Объекты изучения теории вероятностей:
В теории игр – монета, игральный кубик, колода карт, рулетка;
В физике – электрон, скорость движения молекул;
В технике – качество изделий производства;
Два склада. На первом складе из к изделий р бракованных, на втором складе из а изделий ь бракованных. Взяли одно изделие. Какова вероятность что оно бракованное.
Вывод: Предметами изучения теории вероятностей могут быть любые материальные объекты или их характеристики, которые образуют массовые явления со случайным характером событий.
1.4. Виды случайных событий.
а) Элементарные – обозначаются заглавной буквой латинского алфавита.-А, В, С Такие случайные события, которые наблюдаются в результате одного простого опыта, проведённого с объектом теории вероятностей.
Пример: бросание одной кости.
б) Сложные события – такие случайные события, которые представляют собой сумму нескольких элементарных случайных событий. (Обозначение – Si).
Пример: бросание двух костей.
Пример: выпадение двойки на двух игральных костях раз при одновременном броске.
в) Благоприятное событие (исход) – такой результат испытаний с объектом, который нас интересует.
Пример: выпадение орла, выпадение решки.
Выпадение 3 при бросании игральной кости.
г) Равновозможные события – несколько событий в данном опыте называются равновозможными, если нет оснований считать какое-либо из них более возможным, чем любое другое.
Пример: Достоверное событие , невозможное событие.
е) Несовместные события.
Несколько событий называются несовместными в данном опыте, если никакие два из них не могут появиться вместе. . (Выпадение «орла» исключает выпадение «решки»).
ж) Совместные события – случайные события, которые могут наблюдаться в одном простом опыте.
Пример: Из ящика вынимают шары разных цветов с захватом сразу двух, при этом захват двух шаров одного цвета – совместное событие.
з) Независимые события – такие случайные события, вероятность наступления которых в одном опыте не влияет на вероятность наступления следующего (аналогичного) опыта.
е) Полная группа событий.
События А1, А2 … образуют полную группу событий в том случае, если в результате испытаний произойдёт хотя бы одно из этих событий.
Пример:
1. При броске на стол 6и-гранного кубика (симметрического, однородного) могут произойти следующие события: выпадение 1, 2, 3, 4, 5, 6. Эти события образуют полную группу событий.
2. Орел или решка при бросании монеты.
1.5. Классическое определение вероятности событий.
Вероятностью наступления события А называется величина Р(А), равная отношению числа благоприятных событий к общему количеству событий и находится по формуле:
P(A) = m/n , где
Р – символ вероятности;
А – благоприятные события;
m – число благоприятных событий
 n – число равновозможных случаев.
n – число равновозможных случаев.
Вероятность наступления случайного события не может превышать единицу.
Примеры: найти вероятность орла или решки.
Найти вероятность выпадения цифры 5 при бросании игральной кости.
Сумма вероятностей всех единственно возможных событий, составляющих полную группу событий должна быть равна 1. Это является критерием проверки правильности решения задач по теории вероятностей.
РS = Р(А1) + Р(А2) +…+ Р(Аn) = 1
В примере: 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.
д) Противоположное событие.
Противоположными событиями называются два несовместных события, образующих полную группу.
Событие противоположное А обозначается Ā.
Р(А) + Р(Ā) = 1
1.6. Статистическое определение вероятности.
Если случайное событие наступает m раз из n испытаний, частотой события А называется отношение
P*(A) = m/n
Вероятностью случайного события называется предел к которому стремится частота события при неограниченном увеличении числа испытаний:
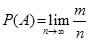
Пример: рождение мальчиков и рождение девочек( Статистическая вероятность Р рождения мальчиков равна 0.512 ).
Одна из центральных теорем теории вероятностей ( теорема Бернулли ) утверждает, что при достаточно общих условиях ( в частности, при большом количестве испытаний ) вероятность, найденная классическим способом ( классическая вероятность ) очень близка к статистической вероятности.
Вызвать 10 студентов.
1.6. Примеры на нахождение классической вероятности.
1. Найти вероятность вытащить белый шар из урны: в урне 3 белых шара, 7 черных шаров.
3. Найти вероятность вытащить два белых шара из урны: в урне 3 белых шара, 7 черных шаров.
2. Найти вероятность комбинации 2+3 при бросании двух игральных костей.








