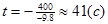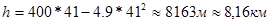Тема урока: Степенная функция, ее свойства и график. Применение свойств степенной функции при решении задач.
15.10.2021
Математика
Группа ПК-271
Тема урока: Степенная функция, ее свойства и график. Применение свойств степенной функции при решении задач.
Цели урока:
Ø обобщить понятие степенной функции, ее свойств путем знакомства со свойствами и графиками различных (в зависимости от показателя степени) видов степенной функции;
Ø обозначить перспективу практического применения знаний о степенной функции.
Образовательная цель: обеспечить повторение, обобщение и систематизацию знаний о степенной функции: виды, свойства и график.
Воспитательная цель: создать условия для применения на уроке математики знаний, полученных в других предметных областях; развивать познавательную активность, самостоятельность, упорство в достижении цели, а так же коммуникативные способности учащихся.
Развивающая цель: продолжить развитие культуры умственной деятельности (анализ, синтез, классификация, планирование), математическая речь
Дидактические средства: учебник Алимов Ш.А. Алгебра и начала анализа: учебник для 10-11 классов общеобразовательных учреждений / Ш.А. Алимов – М.: Просвещение, 2016 Уважаемые студенты!
Для достижения цели занятия вам рекомендуется организовать самообразовательную деятельность, опираясь на предложенный план работы.
План работы.
1. Запишите в тетрадь число, аудиторная работа, тему урока
2. Прочтите материал §6 в учебнике https://znayka.cc/uchebniki/10-klass/algebra-10-11-klass-alimov-kolyagin-bazovyj-i-uglublennyj-urovni/
3. Просмотрите материал видеоролика по ссылке:
https://www.youtube.com/watch?v=z80fU8VeSk4
4. Проработайте следующий материал:
Для начала вспомним определение функции:
Вопрос 1: Что такое функция?
Ответ: Функция (отображение, оператор, преобразование) — соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу первого множества соответствует один и только один элемент второго множества.
Вопрос 2: Какие функции Вы знаете?
Ответ:
Ø Прямая пропорциональность.
Ø Линейная функция.
Ø Обратная пропорциональность.
Ø Квадратичная функция.
Ø Степенная функция.
Ø Показательная функция.
Ø Логарифмическая функция.
Ø Тригонометрические функции.
Ø Обратные тригонометрические функции.
Все выше перечисленные функции относятся к элементарным функциям.
Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций. Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения.
Вопрос 3: Что называется графиком функции?
Ответ:
Ø Это геометрическое понятие в математике, дающее представление о геометрическом образе функции.
Ø В случае использования прямоугольной системы координат, график функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y), которые связаны отображаемой функцией или проще множество точек координатной плоскости, абсциссы которых составляют область определения функции, а ординаты соответствующие значения функции.
Ø Изучение любой функции завершается построением графика этой функции.
Задание: Обратите внимание, на эскизе представлен некий пейзаж. Постарайтесь среди данных линий найти графики функций.
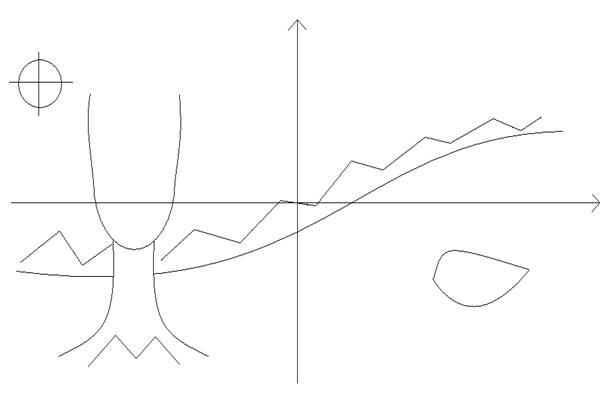
Вопрос 3: Так любое ли множество точек на координатной плоскости задает график функции?
Ответ:
Нет, только такое множество, где каждому значению аргумента соответствует только одно значение функции
Посмотрите, насколько значимо изучение функции! Как мы видим на эскизе, графики функций встречаются не только в математике, но и в природе (горы, леса, деревья) – все, что нас окружает, состоит из графиков функций.
Вопрос: А какие из этих линий относятся к графикам степенных функций?
Теперь давайте вспомним следующие функции, их графики и свойства:
y=x², y=x³, y=1/x ,y=√x или y=x½ , y=x
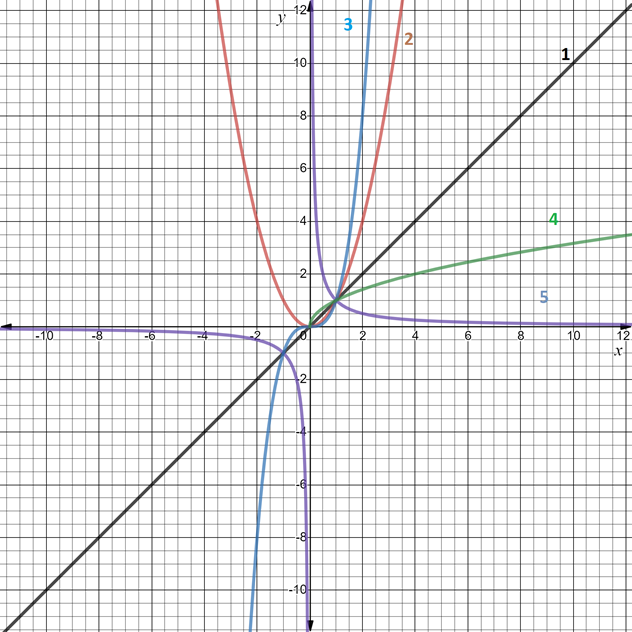
На рисунке изображены графики ряда степенных функций, обозначенные цифрами от 1 до 5). Давайте вспомним:
Ø названия графиков и их соответствие алгебраической записи функции;
Ø свойства изображенных функций (область определения, область значений, четность/нечетность).
1. Степенная функция.
И так, мы вплотную приблизились к пониманию степенной функции.
3.1 Степенная функция — это функция вида y = x p , где p — заданное действительное число (показатель степени).
Ø К степенным функциям часто относят и функцию вида y = kxp , где k — некоторый (ненулевой) коэффициент.
Ø На практике показатель степени почти всегда является целым или рациональным числом.
Ø Если показатель степени — целое число, то можно рассматривать степенную функцию на всей числовой прямой (кроме, возможно, нуля).
Ø Графики степенной функции при натуральном показателе p (= n , принадлежит множеству N – натуральных чисел) называются параболами порядка n.
Ø При p =1 получается y=kx, называемая прямой пропорциональной зависимостью.
Ø Графики функций вида y = xn где n — натуральное число, называются гиперболами порядка n.
Ø При p =-1 получается функция y = x -1 или y =1/ x называемая обратной пропорциональной зависимостью.
Ø Если p =1/ n ,то функция есть арифметический корень степени n.
3.2 Свойства степенной функции:
1. Если показатель p = 2n — четное натуральное число:
1.1. область определения — все действительные числа, т. е. множество R;
1.2. множество значений — неотрицательные числа, т. е. y ≥ 0;
1.3. функция четная;
1.4. функция является убывающей на промежутке x ≤ 0 и возрастающей на промежутке x ≥ 0.
1.4.1. Пример функции с показателем p = 2n: y = x4 , y = x 16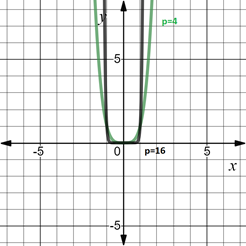 
2. Если показатель p = 2n - 1 — нечетное натуральное число:
2.1. область определения — множество R;
2.2. множество значений — множество R;
2.3. функция нечетная;
2.4. функция является возрастающей на всей действительной оси.
2.4.1. Пример функции с показателем p = 2n - 1: y = x5 и y = x 17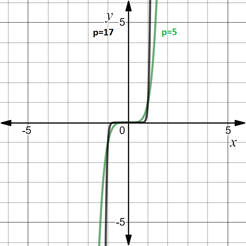 
3. Если показатель p = -2n, где n — натуральное число:
3.1. область определения — множество R, кроме x = 0;
3.2. множество значений — положительные числа y > 0;
3.3. функция четная;
3.4. функция является возрастающей на промежутке x < 0 и убывающей на промежутке x > 0.
3.4.1. Пример функции с показателем p = -2n: y = 1/x2 и y = 1/x16
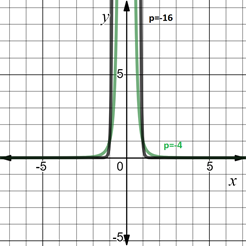
4. Если показатель p = -(2n - 1), где n — натуральное число:
4.1. область определения — множество R, кроме x = 0;
4.2. множество значений — множество R, кроме y = 0;
4.3. функция нечетная;
4.4. функция является убывающей на промежутках x < 0 и x > 0.
4.4.1. Пример функции с показателем p = -(2n - 1): y = 1/x3 и y = 1/x17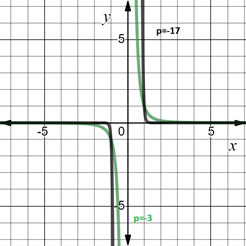 
5. Если показатель p — положительное действительное нецелое число:
5.1. область определения зависит от четности знаменателя;
5.2. множество значений зависит от четности знаменателя;
5.3. функция является возрастающей/убывающей в зависимости от четности знаменателя;
5.3.1. Пример функции с показателем p, где p — положительное действительное нецелое число: y = x 1/3 и y = x4/3.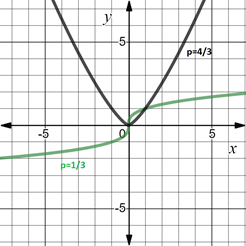 
6. Если показатель p — отрицательное действительное нецелое число:
6.1. область определения — зависит от четности знаменателя и числителя, но x≠0;
6.2. множество значений — зависит от четности знаменателя и числителя, но y≠0;
6.3. функция является убывающей на промежутке x > 0.
6.3.1. Пример функции с показателем p, где p — отрицательное действительное нецелое число: y = x -4/3 и y = x -1/3.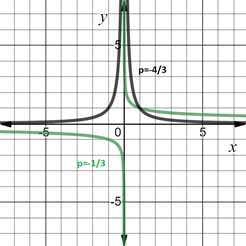 
5. Разберите и запишите в тетрадь задачи
4.1 Задача 1.
Рассмотрим задачу из физики (пример практического применения степенных функций):
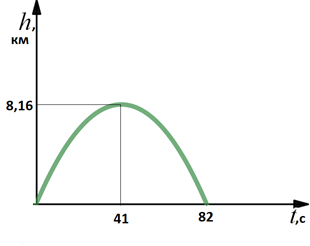
На учебном полигоне произведён выстрел из зенитного орудия в вертикальном направлении. Требуется определить наибольшую высоту подъёма снаряда h, время подъёма t 1 и время падения t 2, если начальная скорость снаряда V 0 = 400 м/с. Сопротивлением воздуха пренебречь.
| Вопрос | Ответ | На доске |
| Что дано в задаче? | Начальная скорость снаряда V0 = 400 м/с, указано направление выстрела. | Дано: V 0 = 400 м/с. |
| Что нужно найти? | Наибольшую высоту подъёма снаряда, время подъёма и время падения. | Найти h , t1 , t2. |
| Записываем решение. | Решение. | |
| Какой функцией выражается закон движения снаряда? | Квадратичной функцией
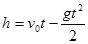 , где g – ускорение свободного падения, g = 9.8 м/с.
|
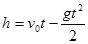g = 9.8 м/с.
|
| А что будет графиком данной функции? | Графиком данной функции является парабола. |
Рисунок |
| Куда будут направлены её ветви? | Ветви параболы направлены вниз. | |
| Где, следовательно, будет наибольшая высота подъёма снаряда? | Наибольшая высота подъёма снаряда будет в вершине параболы. | |
| Что необходимо знать для нахождения наибольшей высоты? | Необходимо найти координаты вершины параболы. | |
| Что мы получим, подставив данные? |
| |
| Как найти время падения снаряда? | Время подъёма снаряда соответствует интервалу возрастания функции и равно 41с. Время падения снаряды соответствует интервалу убывания функции и равно времени подъёма, так как график функции симметричен относительно прямой, проходящей через вершину параболы. | |
| Ответ: | Ответ: h = 8.16 км; t 1 = t 2 ≈ 41c. | |
; 
4.2 Задача 2.
Рассмотрим задачу из экономики с использованием степенной функции:
Вкладчик поместил в банк 1000р. Банк ежегодно выплачивает вкладчику 3% от суммы вклада. Какую сумму денег s получит вкладчик через 2 года?
Решение: (проводится совместно с учениками на доске).
| Вопрос | Ответ | На доске |
| Что нам дано? | Первоначальная сумма денег (s0), Число процентов, начисляемых банком в год (r), Число лет, в течении которых деньги находились в банке (T) | Дано: s0 =1000 r =3% T =2 года |
| Что нужно найти? | Сумму денег (S) | Найти: S-? |
| Вычислим сумму по формуле сложных процентов (степенная функция) | Подставим данные и найдем S | Решение:
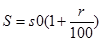 T
S= 1000 (1+0.03)2= =1000*(1.03)2=
=1000*1.6=1060 р.
|
| Записываем ответ | Ответ: S=1060 р. |
Домашнее задание
1. Проработать материал урока,
2. Изучить §6 электронного учебника https://znayka.cc/uchebniki/10-klass/algebra-10-11-klass-alimov-kolyagin-bazovyj-i-uglublennyj-urovni/
Итоги работы и вопросы присылайте преподавателю личным сообщением по адресу https://vk.com/id403066777 до 19.10.2021
Преподаватель Лисица Елена Петровна
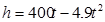
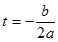