Тема урока: Повторение по теме «Окружность». Анализ контрольной работы.
14 мая 2020 год
Геометрия, 8-А класс
Добрый день!
Ребята, сегодня на уроке мы проводит обобщение и повторение изученного материала.
Тема урока: Повторение по теме «Окружность». Анализ контрольной работы.
Вам необходимо:
1. Записать в тетрадь число, классная работа и перенести тему урока
2. Прослушать анализ контрольной работы (голосовое сообщение в беседе)
3. Выполнить самопроверку контрольной работы (материалы в беседе будут размещены)
4. Повторить п.71, п.72,п.73 из учебника
5. Выполнить задания 1-12 теста Вариант 2
Домашнее задание:
1. Повторить п.63, п.59, п.73, п.65, п.73, п.68, п69, п.71
2. Выполнить задания 13-24 теста Вариант 2
Уважаемые ребята!
Фото выполненной работы отправлять в личные сообщения учителю на страницу ВКонтакте: https://vk.com/id403066777
Вариант 2
1) Расстояние от центра окружности до прямой меньше радиуса окружности. Тогда окружность и прямая имеют общих точек
a) 0 b) 1 c) 2 d) 3 e) определить невозможно
2) AB и ВС – отрезки касательных, проведенных из точки В к окружности с центром О. ОB = 10 см, AO = 5 см. Чему равен ∠AOC?
a) 30° b) 60° c) 90° d) 120° e) 150°
3) Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВ, если ∠АОВ = 60°, а r = 12 см.
a) 6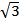 
см b) 12 см c) 12 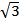см d) 24 см e) 36 см
4) ∠ABC вписан в окружность. Найдите величину дуги AВ, если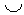 
BC = 112°, а ∠ABC = 78°.
a) 92° b)156° c)170° d)184° e)209°
5) Точки M, N и K лежат на окружности с центром в точке О. Найдите величину угла NОK, если ∠NMK = 70°.
a) 70° b)35° c)90° d)105° e)140°
6) Найдите величину угла ВАС, если АВ – диаметр окружности , точка С лежит на этой окружности, а градусная мера дуги АС равна 80°.
a)100° b)80° c)40° d)50° e)160°
7) Центр описанной окружности лежит на стороне AC треугольника ABC. Найдите сторону АB треугольника, если AC = 12 см, ∠ACB = 60°.
a) 4 см b) 6 см c) 6 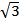см d) 7,5 см e) 9 см
8) Углы MKN и MPN вписаны в окружность с центром в точке О. Найдите величину ∠MKN , если ∠MPN = 120°
a) 15° b) 30° c) 60° d) 90° e) 120°
9) Найдите длину отрезка ED, если хорды AB и CD пересекаются в точке Е.
AE = 0,2 см, BE = 0,5 см, CE = 0,4 см.
a) 0,16 см b) 0,25 см c) 0,3 см d) 0,35 см e) 1 см
10) Сколько утверждений неверны?
1) В любой ромб можно вписать окружность.
2) В любой прямоугольник можно вписать окружность.
3) Радиус окружности, описанной около прямоугольного треугольника, равен половине суммы катетов.
4) Центром окружности, вписанной в треугольник, является точка пересечения биссектрис.
5) Радиус окружности, описанной около треугольника, вычисляется по формуле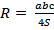 
( a, b, c – стороны треугольника, S – его площадь) .
a)одно b)два c)три d)четыре e)пять
11) Радиус окружности, описанной около равностороннего треугольника, равен 12 см. Найдите радиус окружности, вписанной в этот треугольник.
a) 3 см b) 4 см c) 6 см d) 8 см e) 10 см
12) Около окружности описана трапеция, боковые стороны которой равны 8 см и 12 см. Найдите среднюю линию этой трапеции.
а) 6 см b) 8 см c) 10 см d) 12см е) 16 см
13) Для того, чтобы вокруг выпуклого четырехугольника ABCD можно было описать окружность, должно выполняться следующее равенство:
a) ∠A + ∠B = ∠C + ∠D
b) AB + CD = BC + AD
c) ∠A + ∠C = ∠B + ∠D
d) AB ∙ CD = BC · AD
e) AC = BD
14) Хорды AB и CD окружности с центром О, пересекаются в точке K. Найдите ∠CKA, если 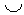AC = 24°, а 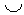BD = 74°.
a) 98° b) 50° c) 49° d) 48° e) 25°
15) Через точку М окружности проведены касательная и хорда. Найдите угол между ними, если хорда стягивает дугу в 80°.
a) 20° b) 40° c) 60° d) 80° e) 90°
16) Найдите величину угла, образованного касательной и секущей, проведенными из точки В к окружности, если 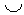CD = 50°, CE = 70° ( С – точка касания, D и E – точки пересечения секущей с окружностью).
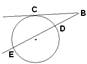
a) 10° b) 20° c) 25° d) 35° e) 60°
17) Из точки А проведены секущие AC и AE. AC пересекает окружность в точках B и C , AE – в точках D и E. ∠СAЕ = 35° , CE = 100°. Найдите BD.
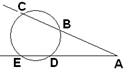
a) 30° b) 35° c) 50° d) 60° e) 70°
18) Найдите длину отрезка CD, если из точки А к окружности проведена касательная AB и секущая AC, AB = 8 см, АС = 16 см.
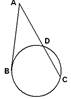
а) 15 см b) 12 см c) 9 см d) 8 см е) 4 см
19) Найдите длину отрезка CD, если из точки М к окружности проведены секущие МВ и MD.
AВ = 4 см, MA = 8 см, MC = 6 см, C – точка пересечения секущей MD с окружностью, А – точка пересечения секущей MB с окружностью.
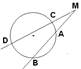
а) 3 см b) 4 см c) 5 
см d) 6 см е) 10 см
20) Треугольник ABC вписан в окружность. CD – диаметр этой окружности. CD перпендикулярен стороне AB треугольника и пересекает ее в точке K. Найти AB,
если CB = 13 см, CK = 12 см.
а) 5 см b) 10 см c) 12 см d) 13 см е) 25 см
21) Две окружности касаются внешним образом. Радиусы этих окружностей относятся как 5:3, а расстояние между их центрами равно 24 см. Найдите диаметр меньшей окружности.
а) 12 см b) 18 см c) 24 см d) 30 см е) 48 см
22) В равнобедренный треугольник ABC (AB = BC) вписана окружность. Точка касания D делит сторону AB в отношении 2:3, считая от вершины А. Найдите сторону CB, если сторона AC равна 12 см.
а) 10 см b) 15 см c) 24 см d) 30 см е) 36 см
23) В прямоугольный треугольник, периметр которого равен 30 см, вписана окружность. Найдите радиус окружности, если его гипотенуза равна 13 см.
а) 2 см b) 2,5 см c) 4 см d) 6 см е) 6,5 см
24) Найдите периметр прямоугольного треугольника, если радиусы его вписанной и описанной окружностей равны соответственно 3 см и 6 см.
а) 18 см b) 24 см c) 27 см d) 30 см е) 36 см