4 Параллельное соединение активного, индуктивного и емкостного элементов
В цепи с параллельным соединением основных пассивных элементов (рисунок 3.18) известно входное напряжение 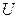 и токи ветвей.
и токи ветвей.
| |
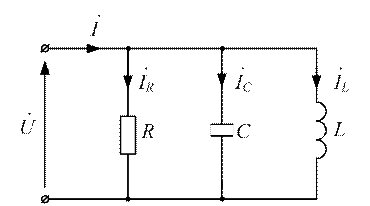
Рисунок 3.18 - Цепь с параллельным соединением элементов 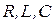 .
.
Определить общий ток, построить векторную диаграмму, найти проводимости.
Для построения векторной диаграммы цепи воспользуемся уравнением первого закона Кирхгофа в векторной форме
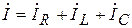 . (3.35)
. (3.35)
Начинаем построение с вектора 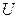 , величина которого является общей для всех элементов цепи. Вектор активного тока
, величина которого является общей для всех элементов цепи. Вектор активного тока 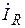 строим совпадающим по фазе с напряжением,
строим совпадающим по фазе с напряжением, 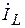 - строим отстающим от него на угол 90°, а
- строим отстающим от него на угол 90°, а 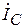 - опережающим его на угол 90°.
- опережающим его на угол 90°.
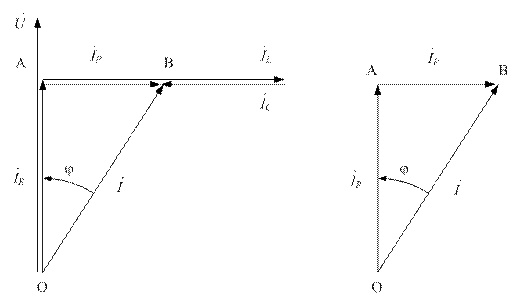
а) б)
Рисунок 3.19 - Векторная диаграмма цепи с параллельным соединением 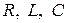 (а) и треугольник тока для случая
(а) и треугольник тока для случая 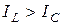 (б).
(б).
Выделим из векторной диаграммы треугольник АОВ, называемый треугольником токов.
Вектор АВ называется реактивной составляющей общего тока
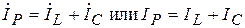
Из треугольника токов получаем соотношение, определяющее общий ток (ток в неразветвленной части цепи) по его составляющим
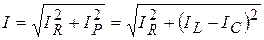 . (3.36)
. (3.36)
Отсюда же получим и выражения для определения составляющих тока и угла между ними, часто используемые в расчетной практике:
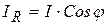 ;
; 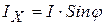 ;
; 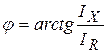 . (3.37)
. (3.37)
Разделив все стороны треугольника токов на напряжение, получим подобный ему треугольник проводимостей (рисунок 3.20).
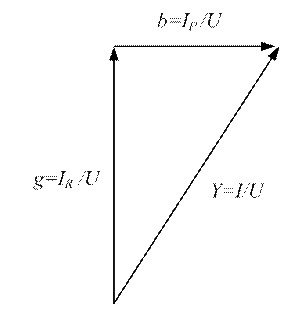
Рисунок 3.20 - Треугольник проводимостей
В этом треугольнике: 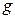 - активная проводимость,
- активная проводимость, 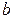 - реактивная проводимость,
- реактивная проводимость,
причем, 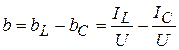 .
.
Полная проводимость цепи - 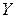 , определяется из треугольника следующим путем
, определяется из треугольника следующим путем
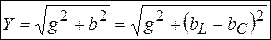 , (3.38)
, (3.38)
где
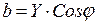 ;
; 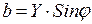 . (3.39)
. (3.39)
Задача № 6
В цепь переменного синусоидального тока с напряжением 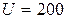 В и частотой
В и частотой 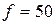 Гц включены три параллельных ветви (рисунок 3.18). Параметры включенных элементов известны:
Гц включены три параллельных ветви (рисунок 3.18). Параметры включенных элементов известны: 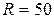 Ом,
Ом, 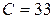 мкФ,
мкФ, 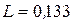 Гн. Определить все токи построить векторную диаграмму.
Гн. Определить все токи построить векторную диаграмму.
Решение
1. Определяем сопротивления реактивных элементов:
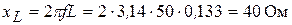 ,
,
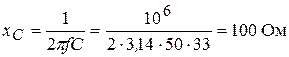 . (3.40)
. (3.40)
2. Токи в параллельных ветвях согласно закона Ома будут равны:
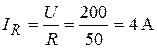 ;
;
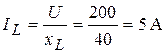 ; (3.41)
; (3.41)
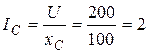 А.
А.
3. В масштабе строим векторную диаграмму напряжения и токов в порядке, описанном выше, ее общий вид показан на рисунке 3.19.
4 Общий ток найдем по выражению (3.36)
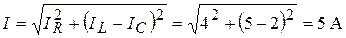 (3.42)
(3.42)
5 Электрические резонансы
Под резонансным режимом работы цепи, содержащей индуктивности и емкости, понимают режим, при котором в результате компенсирующего действия L и C цепь в целом носит чисто активный характер. Поэтому напряжение и ток на входе цепи совпадает по фазе и реактивная мощность равна нулю.
В схеме последовательного соединения катушки и конденсатора наблюдается резонанс напряжений, а в схеме параллельного их соединения - резонанс токов.
3.5.1 Резонанс напряжений
Рассмотрим цепь, в которой установился режим резонанса напряжений (рисунок 3.21).
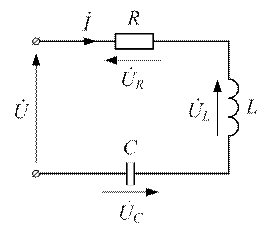
Рисунок 3.21 - Схема цепи с резонансом напряжений
Пусть известны параметры цепи R, L, C и угловая частота резонанса 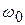 . Найдем результирующее сопротивление цепи, ток, напряжения на элементах, коэффициент мощности и резонансный коэффициент (добротность цепи). Построим векторную диаграмму.
. Найдем результирующее сопротивление цепи, ток, напряжения на элементах, коэффициент мощности и резонансный коэффициент (добротность цепи). Построим векторную диаграмму.
Условием резонанса напряжений является равенство индуктивного и емкостного сопротивлений
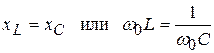 (3.43)
(3.43)
При выполнении этого условия реактивное сопротивление цепи станет равным нулю 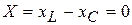 , а полное сопротивление примет минимальное значение равное
, а полное сопротивление примет минимальное значение равное
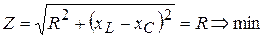 . (3.44)
. (3.44)
Ток цепи достигается максимального значения
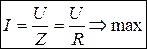 . (3.45)
. (3.45)
Напряжение на индуктивности и емкости будут равны (из условия (3.43))
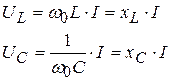 (3.46)
(3.46)
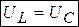 .
.
Поэтому результирующее напряжение станет равным активному напряжению
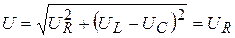 ,
, 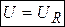 . (3.47)
. (3.47)
В соответствии с выражениями (3.46) и (3.47) векторная диаграмма примет вид, показанный на рисунок 3.22.
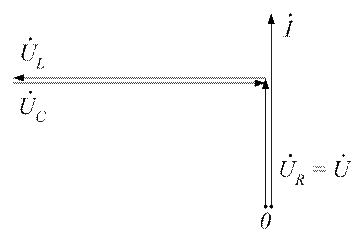
Рисунок 3.22 - Векторная диаграмма резонанса напряжений
Коэффициент мощности при резонансе равен единице
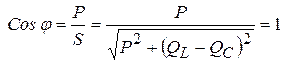
так, как реактивные мощности 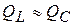 полностью компенсирует друг друга, то есть
полностью компенсирует друг друга, то есть
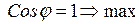 . (3.48)
. (3.48)
Резонансный коэффициент (добротность) определяется отношением
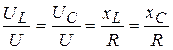 . (3.49)
. (3.49)
При 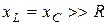 напряжения на индуктивности и емкости окажутся значительно большими, чем приложенное к цепи напряжение
напряжения на индуктивности и емкости окажутся значительно большими, чем приложенное к цепи напряжение
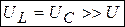 . (3.50)
. (3.50)
Задача № 7
В цепи с последовательным соединением катушки и конденсатора (рисунок 3.23) по показаниям приборов ток 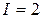 А, напряжение на зажимах цепи
А, напряжение на зажимах цепи 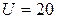 В, напряжение на зажимах конденсатора
В, напряжение на зажимах конденсатора 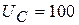 В. В цепи имеет место режим резонанса на частоте 50 Гц.
В. В цепи имеет место режим резонанса на частоте 50 Гц.
Определить: емкость конденсатора С; активное сопротивление катушки 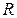 и ее индуктивность
и ее индуктивность 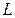 ; напряжение на зажимах катушки
; напряжение на зажимах катушки 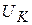 . Построить векторную диаграмму.
. Построить векторную диаграмму.
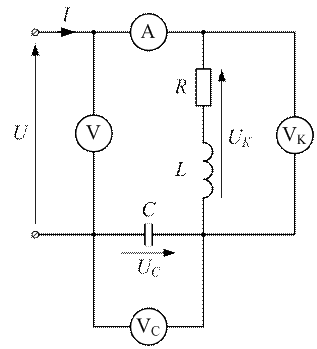
Рисунок 3.23 - Последовательная резонансная цепь
Решение
1. Определим реактивное сопротивление элементов цепи из условия резонанса напряжений
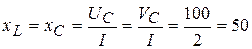 Ом (3.51)
Ом (3.51)
2. Тогда емкость конденсатора и индуктивность катушки:
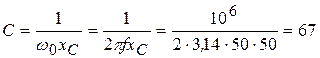 мкФ;
мкФ;
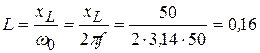 Гн. (3.52)
Гн. (3.52)
3. Определяем полное сопротивление цепи, равное при резонансе активному сопротивлению катушки:
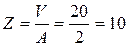 Ом;
Ом;
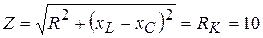 Ом. (3.53)
Ом. (3.53)
4 Определим напряжение на зажимах катушки:
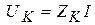 , где
, где 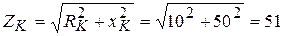 Ом, откуда
Ом, откуда
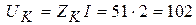 В. (3.54)
В. (3.54)
Реактивная составляющая напряжения на катушке равна
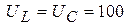 В.
В.
Активная составляющая напряжения на катушке равна
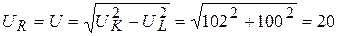 (3.55)
(3.55)
5. Для построения векторной диаграммы выбираем масштабы:
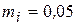 А/мм,
А/мм, 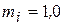 В/мм.
В/мм.
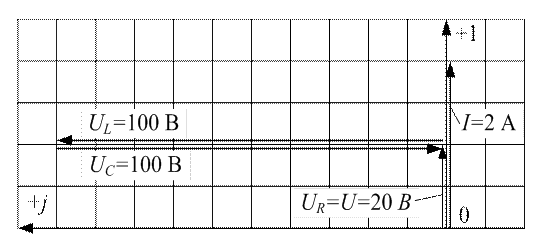
Рисунок 3.24 - Векторная диаграмма
3.5.2 Резонанс токов
Рассмотрим цепь, в которой установился режим резонанса токов (рисунок 3.25). Пусть известны проводимости цепи 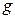 ,
, 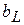 ,
, 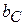 и напряжение на ее входе
и напряжение на ее входе 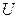 . Найдем результирующую проводимость цепи, токи в ветвях, коэффициент мощности. Построим векторную диаграмму.
. Найдем результирующую проводимость цепи, токи в ветвях, коэффициент мощности. Построим векторную диаграмму.
Условием резонанса токов является равенство реактивных проводимостей катушки и конденсатора, поэтому общая реактивная проводимость цепи равна нулю 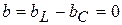 , а полная проводимость равна активной проводимости
, а полная проводимость равна активной проводимости
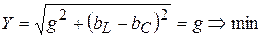 . (3.56)
. (3.56)
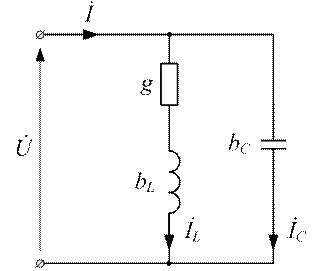
Рисунок 3.25 - Схема цепи с резонансом токов
Ток в неразветвленной части цепи будет тоже минимальным и носить чисто активный характер
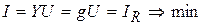 . (3.57)
. (3.57)
Реактивные составляющие токов в ветвях 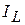 и
и 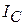 равны, так как равны реактивные проводимости
равны, так как равны реактивные проводимости 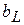 ,
, 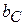 и могут быть значительно больше общего тока:
и могут быть значительно больше общего тока:
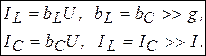 (3.58)
(3.58)
Ток катушки 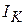 определится на векторной диаграмме (рисунок 3.26) геометрической суммой активной
определится на векторной диаграмме (рисунок 3.26) геометрической суммой активной 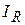 и реактивной
и реактивной 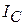 составляющих токов или аналитически:
составляющих токов или аналитически:
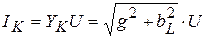 , (3.59)
, (3.59)
где 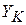 - проводимость ветви с катушкой.
- проводимость ветви с катушкой.
Коэффициент мощности найдем здесь через токи
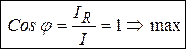 . (3.60)
. (3.60)
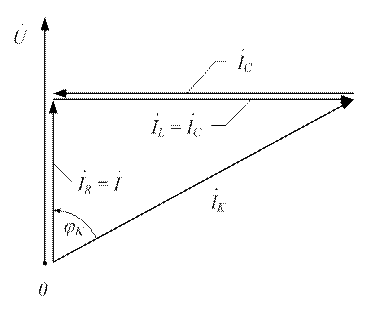
Рисунок 3.26 - Векторная диаграмма резонанса токов
Задача № 8
К зажимам цепи (рисунок 3.27) подведено синусоидальное напряжение величиной 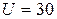 В и частотой
В и частотой 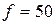 Гц.
Гц.
Какой величины емкость необходимо подключить параллельно катушке, параметры которой 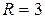 Ом и
Ом и 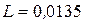 Гн, чтобы в цепи наступил резонанс?
Гн, чтобы в цепи наступил резонанс?
Определить все токи и построить векторную диаграмму для данного режима.
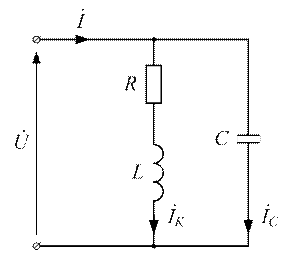
Рисунок 3.27 - Цепь с параллельным соединением 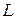 и
и 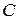
Решение
1. Определяем индуктивное и полное сопротивление катушки
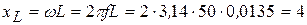 Ом,
Ом,
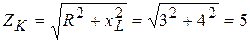 Ом. (3.61)
Ом. (3.61)
2. Тогда ток в катушке
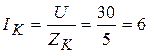 А. (3.62)
А. (3.62)
Активная и реактивная составляющие этого тока будут равны:
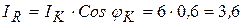 А,
А,
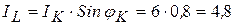 А, (3.63)
А, (3.63)
где
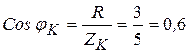 ,
, 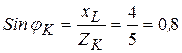
3. Из условия резонанса имеем
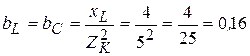 См.
См.
Определим емкостное сопротивление
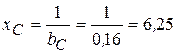 Ом. (3.64)
Ом. (3.64)
4 Емкость и ток, проходящий через конденсатор
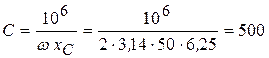 мкФ,
мкФ, 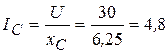 А. (3.65)
А. (3.65)
5. Векторную диаграмму строим в масштабах: 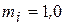 А/мм,
А/мм, 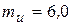 В/мм.
В/мм.
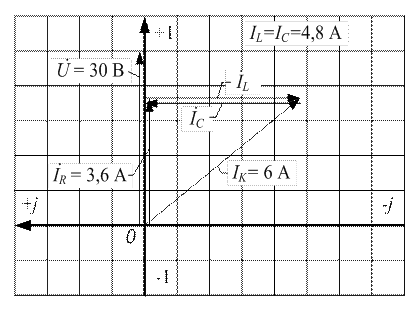
Рисунок 3.28 - Векторная диаграмма для параллельного соединения 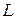 и
и 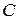
6 Расчет цепей синусоидального переменного тока символическим методом
Все методы расчета, разработанные для цепей постоянного тока, пригодны и для цепей синусоидального тока, но при этом необходимо оперировать комплексными значениями электрических величин, т.е. вести расчет символическим методом.
Рассмотрим пример расчета электрической цепи при помощи комплексных чисел.
Задача № 9
Дана схема представленная на рисунке 3.29. Параметры ее следующие:
E=220 В; f=50 Гц; C1=637 мкФ; C2=300 мкФ; L3=15,9 мГн; R1=2 Ом; R2=3 Ом; R3= 4 Ом; Rv=∞; Ra=0; (Rv и Ra – внутренние сопротивления вольтметра и амперметра, соответственно).
Найти:
1 Все токи.
2 Проверить токи на баланс токов.
3 Проверить токи на баланс мощности;
4 Все напряжения на элементах цепи.
5 Проверить напряжения на баланс напряжений.
6 Показания вольтметра и амперметра.
7 Построить топографическую диаграмму цепи.
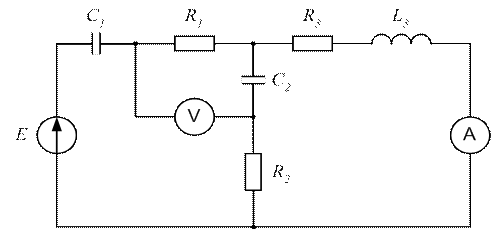
Рисунок 3.29 - Исходная схема
Решение
Расчет будем вести методом линейных преобразований, рассмотренным ранее на примере цепи постоянного тока (раздел 3.3). Метод основан, на свертывании сложной цепи с помощью формул последовательного, параллельного, смешанного соединений, а также перехода от треугольника к звезде сопротивлений. Полученное решение последовательно развертывается до заданной цепи.
Данный способ возможен, когда все ветви цепи пассивны и в цепи имеется лишь один источник энергии.
1. Определяем реактивные сопротивления участков цепи
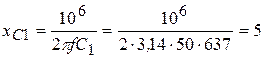 Ом,
Ом,
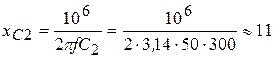 Ом, (3.66)
Ом, (3.66)
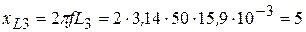 Ом.
Ом.
2. Определяем полные сопротивления ветвей цепи по выражению
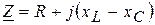
Согласно рисунку 3.30, имеем,
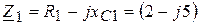 Ом,
Ом,
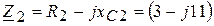 Ом,
Ом,
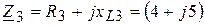 Ом. (3.67)
Ом. (3.67)
3. Составляем расчетную схему
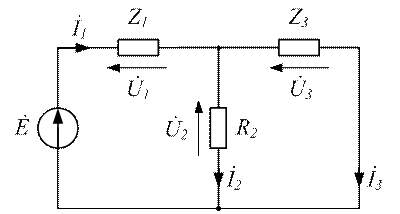
Рисунок 3.30 - Расчетная схема
Из расчетной схемы исключен вольтметр, его сопротивление равно бесконечности, и амперметр, его сопротивление равно нулю.
4 Определяем эквивалентное сопротивление цепи
По схеме (рисунок 3.30) найдем ее входное эквивалентное сопротивление относительно входных зажимов цепи
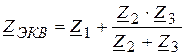 (3.68)
(3.68)
Составляющие выражения (3.68) находим так;
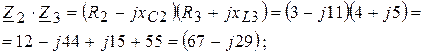
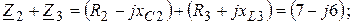
подставляя в (3 .68), получаем
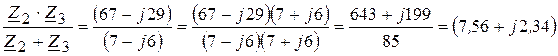
Окончательно имеем
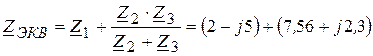 , (3.69)
, (3.69)
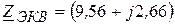 Ом.
Ом.
5. Размечаем условно-положительные направления токов и напряжений
На схеме (рисунке 3.30) размечаем стрелки токов в комплексной форме. Стрелки комплексных напряжений размечаем против стрелок токов.
6. Определяем ток 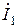
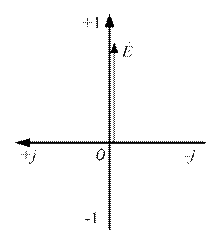 Рисунок 3.31 – К определению напряжений
Рисунок 3.31 – К определению напряжений
|
Определяем ток в первой ветви 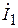 . Выражаем заданную ЭДС
. Выражаем заданную ЭДС 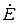 в комплексной форме. Если не задана начальная фаза ЭДС, ее можно принять равной нулю и располагать вектор ЭДС, совпадающим с положительным направлением действительной оси комплексной плоскости.
в комплексной форме. Если не задана начальная фаза ЭДС, ее можно принять равной нулю и располагать вектор ЭДС, совпадающим с положительным направлением действительной оси комплексной плоскости.
В этом случае мнимая составляющая комплексного числа будет отсутствовать (рисунок 3.31) и входная ЭДС может быть записано в форме:
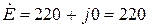 В
В
По закону Ома получаем:
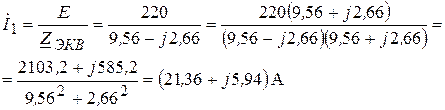 (3.70)
(3.70)
7. Проверяем найденный ток 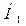 на баланс мощности
на баланс мощности
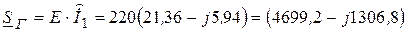 ВА,
ВА,
где 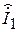 - сопряженное комплексное значение тока
- сопряженное комплексное значение тока 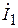 .
.
Нагрузка цепи потребляет мощность
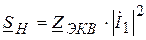
Квадрат модуля тока
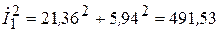
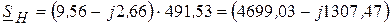 ВА.
ВА.
Ошибки по балансу мощности не превышают 1% процента, значит ток 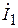 найден верно.
найден верно.
8. Определяем напряжение 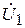
Согласно рисунку 3.30, имеем:
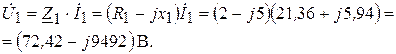 (3.71)
(3.71)
9. Определяем напряжения 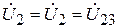
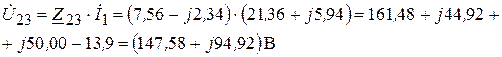 (3.72)
(3.72)
Проверяем найденные напряжения на баланс напряжений согласно второму закону Кирхгофа:
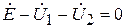
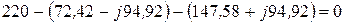 (3.73)
(3.73)
Баланс сошелся, значит напряжение 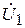 и
и 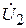 найдены верно.
найдены верно.
10. Определяем 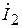
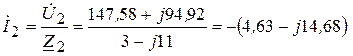 А (3.74)
А (3.74)
Ток получился отрицательным. Это значит, что в действительности ток во второй ветви протекает против направления стрелки и стрелка, была размечена в начале расчета не правильно, но исправлять стрелку не нужно, это приводит обычно к ошибкам в дальнейшем расчете.
11. Определяем ток 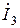
По закону Ома получаем,
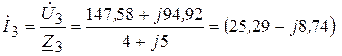 А (3.75)
А (3.75)
12. Проверяем токи на баланс токов
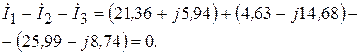 (3.76)
(3.76)
13. Проверяем токи на баланс мощности
Источник энергии вырабатывает мощность:
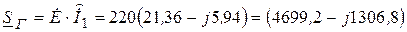 ВА,
ВА,
где 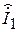 - сопряженное комплексное значение тока.
- сопряженное комплексное значение тока.
Нагрузка цепи потребляет мощность -
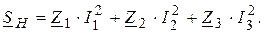
Квадраты модулей токов в ветвях:
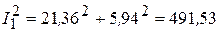
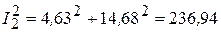
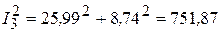
Составляющие мощности:
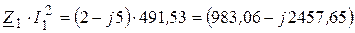 ,
,
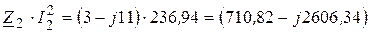 ,
,
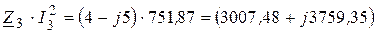 . (3.77)
. (3.77)
Итого: 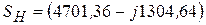 BA .
BA .
Сходимость баланса мощности

от величины 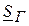 .
.
Баланс мощности сошелся, токи найдены правильно.
13. Определяем напряжения на элементах цепи
Для этого повторяем схему заданной цепи и размечаем на ней все токи и напряжения. Буквами обозначим узлы схемы и точки, отделяющие элементы цепи друг от друга, начиная с низшего потенциала.
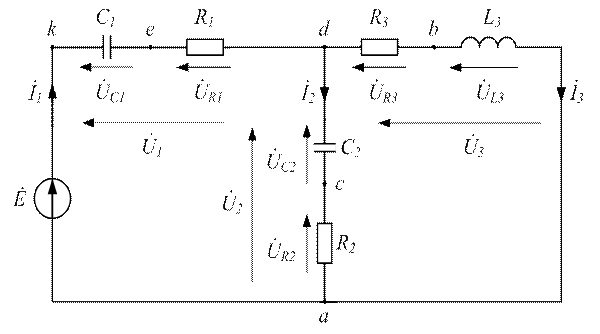 Рисунок 3.32 - Напряжения на элементах цепи
Рисунок 3.32 - Напряжения на элементах цепи
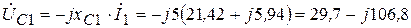 В
В
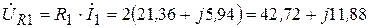 В,
В,
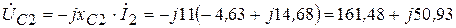 В, (3.78)
В, (3.78)
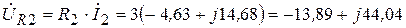 В,
В,
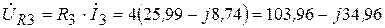 В,
В,
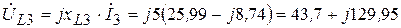 В.
В.
На основании (3.78) действующие значения напряжений будут равны:
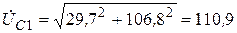 В,
В,
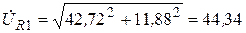 В,
В,
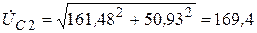 В, (3.79)
В, (3.79)
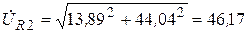 В,
В,
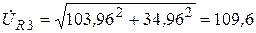 В,
В,
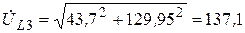 В.
В.
15. Производим проверку на баланс напряжений
Проверяем полученные напряжения на баланс напряжений, подставив полученные значения комплексов напряжений на элементах цепи в уравнения, составленные по 2-му закону Кирхгофа.
Первое уравнение:
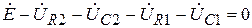
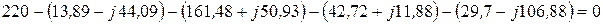
Второе уравнение:
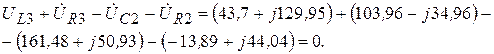 (3.80)
(3.80)
16. Определяем действующие значения токов
Из выражений (3.77) получим:
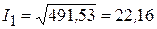 А,
А,
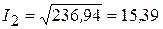 А, (3.81)
А, (3.81)
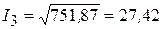 А,
А,
17. Определяем показания вольтметра
На схеме (рисунок 3.33) изображен участок цепи с включенным вольтметром, из нее имеем:
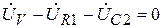 ,
,
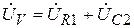 . (3.82)
. (3.82)
Подставляем в (3.82) значения (3.78).
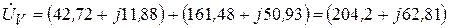 В (3.83)
В (3.83)
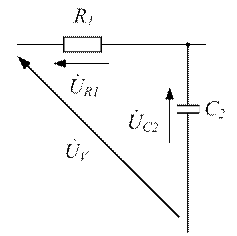
Рисунок 3.33 - Участок цепи (замкнутый контур) с напряжением
Вольтметра 
Показания вольтметра будут
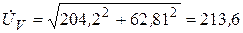 . (3.84)
. (3.84)
Результаты расчета приведены в таблице 3.1.
Таблица 3.1 - Результаты расчета токов и напряжений
| Обозначения | Комплексы | Величины |
| I1 | 21,36 + j5,94 | 22.16 A |
| I2 | - 4,63 + j14,68 | 15.39 A |
| I3 | 25,99 - j8,74 | 27,42 A |
| U1 | 72,42 – j94,92 | 119,2 A |
| U2=U3 | 147,58 + j94,92 | 173,22 B |
| UC1 | 29,7 - j106,8 | 110,9 B |
| UR1 | 42,72 + j11,88 | 44,34 B |
| UC2 | 161,48 + j50,93 | 169,4 B |
| UR2 | - 13,89 + j44,04 | 46,17 B |
| UR3 | 103,96 - j34,94 | 109,6 B |
| UL3 | 43,7 + j129,95 | 137,1 B |
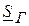
| 4699,2 - j1306,8 | 4868,8 BA |
| PГ | 4699,2 Вт | |
| QГ | 1306,8 вар |
Показания вольтметра 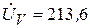 B, показания амперметра
B, показания амперметра 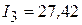 А.
А.
18. Строим векторную диаграмму токов (рисунок 3.34)
а) Выбираем масштаб для векторов токов 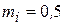 A/мм;
A/мм;
б) Наносим комплексные оси: вертикальная - ось действительных чисел, горизонтальная - ось мнимых чисел;
в) Строим в масштабе, согласно данным таблицы 3.1, векторы токов 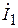 ,
, 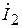 и
и 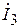 . Вектор тока
. Вектор тока 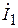 на векторной диаграмме должен равняться геометрической сумме векторов токов
на векторной диаграмме должен равняться геометрической сумме векторов токов 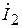 и
и 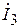 , так как
, так как 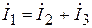 по первому закону Кирхгофа.
по первому закону Кирхгофа.
19. Строим векторную диаграмму напряжений (рисунок 3.34)
а) Выбираем масштаб для векторов напряжений: 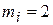 B/мм;
B/мм;
б) Строим в масштабе, согласно данным таблицы 3.1, векторы напряжений: 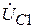 ,
, 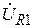 ,
, 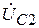 ,
, 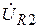 ,
, 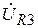 ,
, 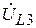 .
.
Вектор 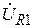 , должен быть параллелен вектору тока
, должен быть параллелен вектору тока 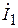 , так, как они совпадают по фазе. Вектор
, так, как они совпадают по фазе. Вектор 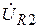 также должен совпадать по фазе с вектором тока
также должен совпадать по фазе с вектором тока 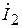 , а
, а 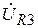 с вектором тока
с вектором тока 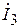 .
.
Вектор 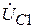 должен быть перпендикулярен к вектору тока
должен быть перпендикулярен к вектору тока 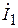 , и отставать от него. Вектор тока
, и отставать от него. Вектор тока 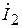 также опережает вектор напряжения
также опережает вектор напряжения 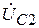 на угол равный 90°. Вектор напряжения
на угол равный 90°. Вектор напряжения 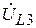 должен быть перпендикулярен к вектору тока,
должен быть перпендикулярен к вектору тока, 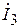 и направлен в сторону опережения от этого тока.
и направлен в сторону опережения от этого тока.
20. Построение топографической диаграммы напряжений
Топографическая векторная диаграмма напряжений строится в следующем порядке (рисунок 3.34):
а) Наносим комплексные оси: вертикальная - ось действительных чисел; горизонтальная - ось мнимых чисел;
б) За начало отсчета системы координат на комплексной плоскости принимаем точку самого низкого потенциала, а соответственно схеме на рисунке 3.33.
в) Строим вектор напряжения 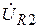 из точки а, и конец вектора обозначаем точкой с;
из точки а, и конец вектора обозначаем точкой с;
г) Из точки с строим вектор напряжения 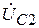 и получаем точку d;
и получаем точку d;
д) Из конца вектора напряжения 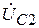 (точки d) строим вектор напряжения
(точки d) строим вектор напряжения 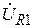 и обозначаем, конец этого вектора точкой е;
и обозначаем, конец этого вектора точкой е;
е) Из точки О строим вектор 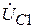 , конец, которого обозначаем точкой к;
, конец, которого обозначаем точкой к;
ж) Точка к должна являться концом вектора э.д.c. 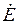 , расположенном на действительной оси чисел, так как согласно 2-му закону Кирхгофа,
, расположенном на действительной оси чисел, так как согласно 2-му закону Кирхгофа, 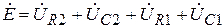 .
.
з) Строим из точки а вектор 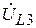 и из полученной точки в вектор
и из полученной точки в вектор 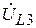 , конец, которого должен совпасть с точкой d на диаграмме, так как
, конец, которого должен совпасть с точкой d на диаграмме, так как 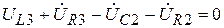 по 2-му закону Кирхгофа;
по 2-му закону Кирхгофа;
и) Соединив точки d и к, получим вектор напряжения 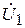 т.к.
т.к. 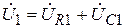 .
.
к) Соединим точку а на диаграмме с точкой d и получим вектор напряжения 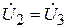 . Вектор
. Вектор 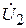 равен геометрической сумме векторов
равен геометрической сумме векторов 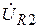 и
и 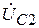 так, как
так, как 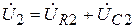 , по второму закону Кирхгофа. Вектор напряжения
, по второму закону Кирхгофа. Вектор напряжения 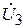 равен геометрической сумме векторов
равен геометрической сумме векторов 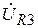 и
и 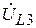 , так, как
, так, как 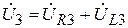 , согласно 2-му закону Кирхгофа.
, согласно 2-му закону Кирхгофа.
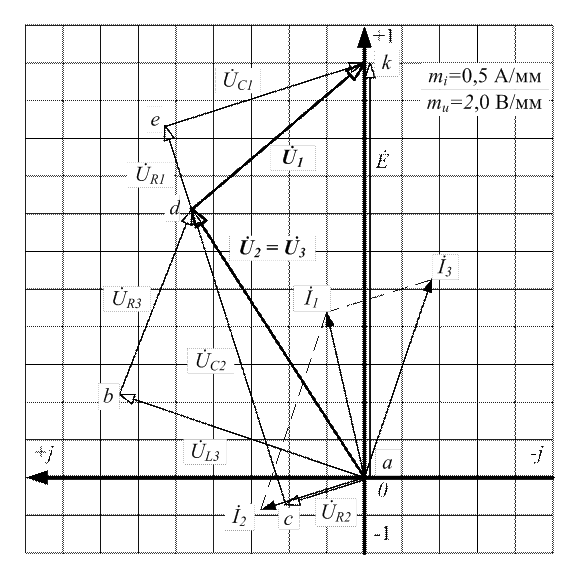 Рисунок 3.34 - Векторная топографическая диаграмма
Рисунок 3.34 - Векторная топографическая диаграмма
7 Варианты контрольных заданий для самостоятельного решения
Для электрической схемы, соответствующей номеру варианта (таблица 3.2) и изображенной на рис. 3.35 - 3.55, по заданным параметрам и ЭДС источника энергии выполнить следующие задания:
1 Определить токи во всех ветвях.
2 Проверить токи на баланс токов.
3 Проверить токи на баланс мощности.
4 Определить напряжение на элементах и ветвях.
5 Построить векторные диаграммы токов и напряжений.
6 Построить топографическую векторную диаграмму.
Таблица 3.2 – Задания для самостоятельного решения
| Вари-ант | Номер рисун-ка | E, В | f, Гц | С1, мкФ | С2, мкФ | С3, мкФ | L1, мГн | L2, мГн | L3, мГн | R1, Ом | R2, Ом | R3, Ом |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 3.35 | 50 | 50 | - | 1000 | - | 31,8 | - | 15,9 | 95 | 10 | 2 |
| 2 | 3.35 | 100 | 60 | - | 1000 | - | 31,8 | - | 6,37 | 95 | 10 | 2 |
| 3 | 3.35 | 120 | 100 | - | 1000 | - | 31,8 | - | 6,37 | 95 | 10 | 2 |
| 4 | 3.35 | 200 | 150 | - | 1000 | - | 31,8 | - | 15,9 | 95 | 10 | 2 |
| 5 | 3.35 | 220 | 200 | - | 1000 | - | 31,8 | - | 15,9 | 95 | 10 | 2 |
| 6 | 3.36 | 50 | 50 | - | - | 1000 | 15,9 | 100 | 115 | 10 | 1 | 100 |
| 7 | 3.36 | 100 | 60 | - | - | 1000 | 15,9 | 100 | 115 | 10 | 1 | 100 |
| 8 | 3.36 | 120 | 100 | - | - | 1000 | 15,9 | 100 | 115 | 10 | 1 | 100 |
| 9 | 3.36 | 200 | 150 | - | - | 1000 | 15,9 | 100 | 115 | 10 | 1 | 100 |
| 10 | 3.36 | 220 | 200 | - | - | 1000 | 15,9 | 100 | 115 | 10 | 1 | 100 |
| 11 | 3.37 | 50 | 50 | 637 | - | - | - | 15,9 | 6,37 | 5 | 10 | 2 |
| 12 | 3.37 | 100 | 60 | 637 | - | - | - | 15,9 | 6,37 | 5 | 10 | 2 |
| 13 | 3.37 | 120 | 100 | 637 | - | - | - | 15,9 | 6,37 | 5 | 10 | 2 |
| 14 | 3.37 | 200 | 150 | 637 | - | - | - | 15,9 | 6,37 | 5 | 10 | 2 |
| 15 | 3.37 | 220 | 200 | 637 | - | - | - | 15,9 | 6,37 | 5 | 10 | 2 |
| 16 | 3.38 | 50 | 50 | 637 | 300 | - | - | - | 15,9 | 2 | 3 | |
| 17 | 3.38 | 100 | 60 | 637 | 300 | - | - | - | 15,9 | 2 | 3 | |
| 18 | 3.38 | 120 | 100 | 637 | 300 | - | - | - | 15,9 | 2 | 3 | |
| 19 | 3.38 | 200 | 120 | 637 | 300 | - | - | - | 15,9 | 2 | 3 | |
| 20 | 3.38 | 220 | 200 | 637 | 300 | - | - | - | 15,9 | 2 | 3 | |
| 21 | 3.39 | 50 | 50 | 637 | 159 | - | - | - | 95 | 5 | 10 | 4 |
| 22 | 3.39 | 100 | 60 | 637 | 159 | - | - | - | 95 | 5 | 10 | 4 |
| 23 | 3.39 | 120 | 100 | 637 | 159 | - | - | - | 95 | 5 | 10 | 4 |
| 24 | 3.39 | 200 | 150 | 637 | 159 | - | - | - | 95 | 5 | 10 | 4 |
| 25 | 3.39 | 220 | 200 | 637 | 159 | - | - | - | 95 | 5 | 10 | 4 |
| 26 | 3.40 | 50 | 50 | 650 | 900 | - | 20 | - | - | 2 | 8 | 3 |
| 27 | 3.40 | 100 | 60 | 650 | 900 | - | 20 | - | - | 4 | 7 | 5 |
| 28 | 3.40 | 120 | 100 | 650 | 900 | - | 20 | - | - | 6 | 11 | 12 |
| 29 | 3.40 | 200 | 150 | 650 | 900 | - | 20 | - | - | 3 | 10 | 7 |
| 30 | 3.40 | 220 | 200 | 650 | 900 | - | 20 | - | - | 18 | 11 | 15 |
| 31 | 3.41 | 50 | 50 | - | 637 | - | 19,1 | - | 31,8 | 10 | - | 10 |
| 32 | 3.41 | 100 | 60 | - | 637 | - | 19,1 | - | 31,8 | 10 | - | 10 |
| 33 | 3.41 | 120 | 100 | - | 637 | - | 19,1 | - | 31,8 | 10 | - | 10 |
| 34 | 3.41 | 200 | 150 | - | 637 | - | 19,1 | - | 31,8 | 10 | - | 10 |
| 35 | 3.41 | 220 | 200 | - | 637 | - | 19,1 | - | 31,8 | 10 | - | 10 |
| 36 | 3.42 | 50 | 50 | - | 318 | - | 15,9 | - | 15,9 | 2 | 10 | 4 |
| 37 | 3.42 | 100 | 60 | - | 318 | - | 15,9 | - | 15,9 | 2 | 10 | 4 |
| 38 | 3.42 | 200 | 150 | - | 318 | - | 15,9 | - | 15,9 | 2 | 10 | 4 |
| 39 | 3.42 | 220 | 200 | - | 318 | - | 15,9 | - | 15,9 | 2 | 10 | 4 |
| 40 | 3.42 | 120 | 100 | - | 318 | - | 15,9 | - | 15,9 | 2 | 10 | 4 |
| 41 | 3.43 | 50 | 50 | - | 318 | - | 9,55 | - | - | 4 | 10 | 4 |
| 42 | 3.43 | 100 | 60 | - | 318 | - | 9,55 | - | - | 4 | 10 | 4 |
| 43 | 3.43 | 120 | 100 | - | 318 | - | 9,55 | - | - | 4 | 10 | 4 |
| 44 | 3.43 | 200 | 150 | - | 318 | - | 9,55 | - | - | 4 | 10 | 4 |
| 45 | 3.43 | 220 | 200 | - | 318 | - | 9,55 | - | - | 4 | 10 | 4 |
| 46 | 3.44 | 50 | 50 | 1000 | - | - | 32 | 15 | - | 11 | 4 | - |
| 47 | 3.44 | 100 | 60 | 1000 | - | - | 32 | 15 | - | 3 | 9 | - |
| 48 | 3.44 | 120 | 100 | 1000 | - | - | 32 | 15 | - | 8 | 12 | - |
| 49 | 3.44 | 200 | 150 | 1000 | - | - | 32 | 15 | - | 16 | 20 | - |
| 50 | 3.44 | 220 | 200 | 1000 | - | - | 32 | 15 | - | 5 | 14 | - |
| 51 | 3.45 | 50 | 50 | 500 | 1000 | - | 30 | - | - | 7 | 4 | 3 |
| 52 | 3.45 | 100 | 60 | 500 | 1000 | - | 30 | - | - | 8 | 5 | 2 |
| 53 | 3.45 | 120 | 100 | 500 | 1000 | - | 30 | - | - | 6 | 7 | 8 |
| 54 | 3.45 | 200 | 150 | 500 | 1000 | - | 30 | - | - | 5 | 3 | 1 |
| 55 | 3.45 | 220 | 200 | 500 | 1000 | - | 30 | - | - | 4 | 9 | 3 |
| 56 | 3.46 | 50 | 50 | 600 | 900 | - | 25 | - | - | 2 | 3 | 4 |
| 57 | 3.46 | 100 | 60 | 600 | 900 | - | 25 | - | - | 7 | 5 | 4 |
| 58 | 3.46 | 120 | 100 | 600 | 900 | - | 25 | - | - | 3 | 2 | 8 |
| 59 | 3.46 | 200 | 150 | 600 | 900 | - | 25 | - | - | 10 | 9 | 6 |
| 60 | 3.46 | 220 | 200 | 600 | 900 | - | 25 | - | - | 2 | 11 | 4 |
| 61 | 3.47 | 50 | 50 | 700 | 450 | 800 | 10 | - | - | 20 | 10 | - |
| 62 | 3.47 | 100 | 60 | 700 | 450 | 800 | 10 | - | - | 17 | 5 | - |
| 63 | 3.47 | 120 | 100 | 700 | 450 | 800 | 10 | - | - | 3 | 11 | - |
| 64 | 3.47 | 200 | 150 | 700 | 450 | 800 | 10 | - | - | 8 | 14 | - |
| 65 | 3.47 | 220 | 200 | 700 | 450 | 800 | 10 | - | - | 21 | 7 | - |
| 66 | 3.48 | 50 | 50 | 1200 | - | - | 12 | 20 | - | 10 | 6 | - |
| 67 | 3.48 | 100 | 60 | 1200 | - | - | 12 | 20 | - | 8 | 3 | - |
| 68 | 3.48 | 120 | 100 | 1200 | - | - | 12 | 20 | - | 4 | 7 | - |
| 69 | 3.48 | 200 | 150 | 1200 | - | - | 12 | 20 | - | 5 | 11 | - |
| 70 | 3.48 | 220 | 200 | 1200 | - | - | 12 | 20 | - | 9 | 7 | - |
| 71 | 3.49 | 50 | 50 | 420 | 900 | - | 8 | - | - | 20 | 7 | - |
| 72 | 3.49 | 100 | 60 | 420 | 900 | - | 8 | - | - | 15 | 3 | - |
| 73 | 3.49 | 120 | 100 | 420 | 900 | - | 8 | - | - | 17 | 8 | - |
| 74 | 3.49 | 200 | 150 | 420 | 900 | - | 8 | - | - | 6 | 4 | - |
| 75 | 3.49 | 220 | 200 | 420 | 900 | - | 8 | - | - | 5 | 8 | - |
| 76 | 3.50 | 50 | 50 | 750 | - | - | 35 | 18 | 10 | 10 | 5 | - |
| 77 | 3.50 | 100 | 60 | 750 | - | - | 35 | 18 | 10 | 8 | 4 | - |
| 78 | 3.50 | 120 | 100 | 750 | - | - | 35 | 18 | 10 | 3 | 7 | - |
| 79 | 3.50 | 200 | 150 | 750 | - | - | 35 | 18 | 10 | 12 | 6 | - |
| 80 | 3.50 | 220 | 200 | 750 | - | - | 35 | 18 | 10 | 3 | 8 | - |
| 81 | 3.51 | 50 | 50 | - | 159 | - | 15,9 | - | 31,8 | 3 | 20 | - |
| 82 | 3.51 | 100 | 60 | - | 159 | - | 15,9 | - | 31,8 | 3 | 20 | - |
| 83 | 3.51 | 120 | 100 | - | 159 | - | 15,9 | - | 31,8 | 3 | 20 | - |
| 84 | 3.51 | 200 | 150 | - | 159 | - | 15,9 | - | 31,8 | 3 | 20 | - |
| 85 | 3.51 | 50 | 50 | - | 159 | - | 15,9 | - | 31,8 | 5 | 10 | - |
| 86 | 3.52 | 50 | 50 | 200 | - | - | 20 | 30 | 40 | 8 | - | - |
| 87 | 3.52 | 100 | 60 | 200 | - | - | 20 | 30 | 40 | 7 | - | - |
| 88 | 3.52 | 120 | 100 | 200 | - | - | 20 | 30 | 40 | 10 | - | - |
| 89 | 3.52 | 200 | 150 | 200 | - | - | 20 | 30 | 40 | 14 | - | - |
| 90 | 3.52 | 220 | 200 | 200 | - | - | 20 | 30 | 40 | 3 | - | - |
| 91 | 3.53 | 50 | 50 | 159 | - | 637 | 25 | 9 | - | 6 | 4 | - |
| 92 | 3.53 | 100 | 60 | 159 | - | 637 | 25 | 9 | - | 6 | 4 | - |
| 93 | 3.53 | 120 | 100 | 159 | - | 637 | 25 | 9 | - | 6 | 4 | - |
| 94 | 3.53 | 200 | 150 | 159 | - | 637 | 25 | 9 | - | 6 | 4 | - |
| 95 | 3.53 | 220 | 200 | 159 | - | 637 | 25 | 9 | - | 6 | 4 | - |
| 96 | 3.54 | 50 | 50 | 1100 | - | - | 8 | 7 | - | 5 | 4 | - |
| 97 | 3.54 | 100 | 60 | 1100 | - | - | 8 | 7 | - | 3 | 9 | - |
| 98 | 3.54 | 120 | 100 | 1100 | - | - | 8 | 7 | - | 11 | 15 | - |
| 99 | 3.54 | 200 | 150 | 1100 | - | - | 8 | 7 | - | 6 | 8 | - |
| 100 | 3.54 | 220 | 200 | 1100 | - | - | 8 | 7 | - | 7 | 12 | - |
к заданиям
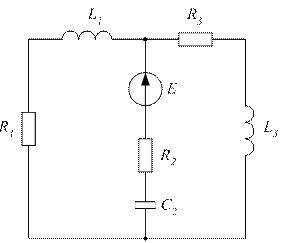 Рисунок 3.35
Рисунок 3.35
| 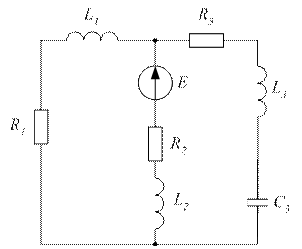 Рисунок 3.36
Рисунок 3.36
|
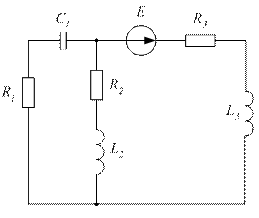 Рисунок 3.37
Рисунок 3.37
| 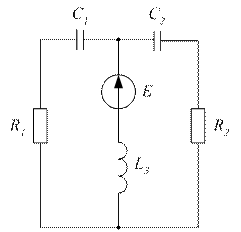 Рисунок 3.38
Рисунок 3.38
|
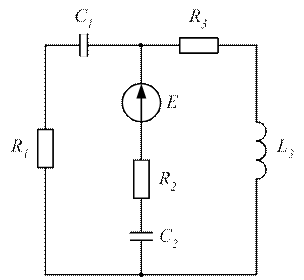 Рисунок 3.39
Рисунок 3.39
| 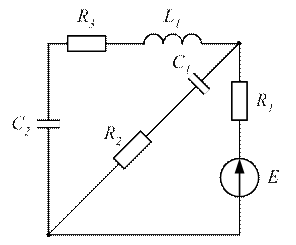 Рисунок 3.40
Рисунок 3.40
|
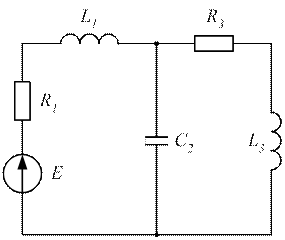 Рисунок 3.41
Рисунок 3.41
| 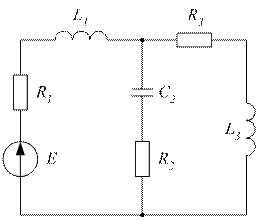 Рисунок 3.42
Рисунок 3.42
|
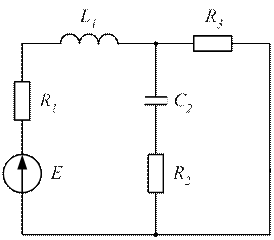 Рисунок 3.43
Рисунок 3.43
|
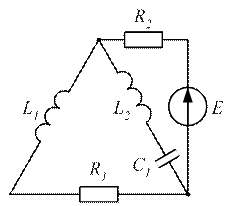 Рисунок 3.44
Рисунок 3.44
|
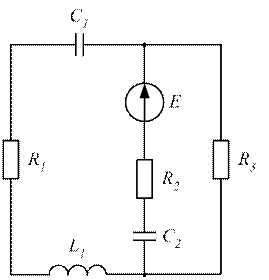 Рисунок 3.45
Рисунок 3.45
|
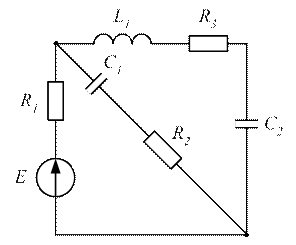 Рисунок 3.46
Рисунок 3.46
|
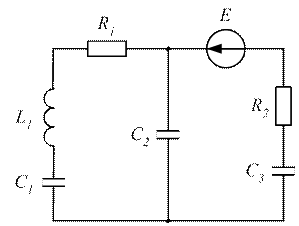 Рисунок 3.47
Рисунок 3.47
| 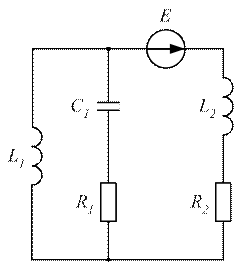 Рисунок 3.48
Рисунок 3.48
|
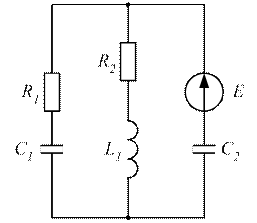 Рисунок 3.49
Рисунок 3.49
|
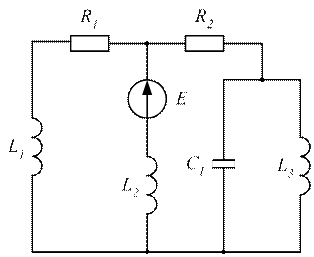 Рисунок 3.50
Рисунок 3.50
|
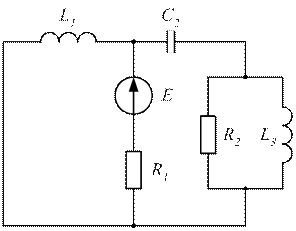 Рисунок 3.51
Рисунок 3.51
|
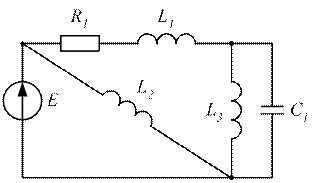 Рисунок 3.52
Рисунок 3.52
|
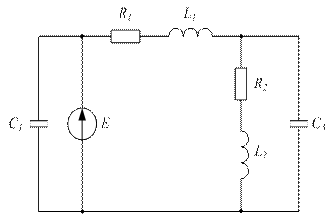 Рисунок 3.53
Рисунок 3.53
|
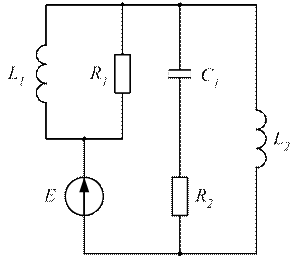 Рисунок 3.54
Рисунок 3.54
|
3.8 Контрольные вопросы
1 Однофазный синусоидальный ток, получение однофазного тока, Период, частота, угловая скорость (определение, обозначение, аналитическая связь между ними). Основные соображения, по которым принят в промышленности переменный ток, изменяющийся по синусоидальной кривой. Стандартная частота промышленного тока и причины, по которым она выбрана.
2 Мгновенное значение переменного тока (определение, обозначение, аналитические выражения и соответствующие графики). Амплитудное значение переменного тока (определение и обозначение).
3 Действующее значение переменного тока любой формы кривой и синусоидальной (определение, вывод формул).
4 Среднее значение переменного тока любой формы кривой и синусоидальной (определение, вывод формул). Коэффициент формы кривой (определение, вывод численной величины его для синусоидального тока, практическое значение).
5 Рассмотреть активный элемент цепи (дать определение ему, вывести аналитическое выражение для Ua при токе i=Imsinwt, показать их на графике, начертить векторную диаграмму).
6 Рассмотреть индуктивный элемент (дать определение ему, вывести формулу для ui при токе i=Imsinwt, показать их на графике, начертить векторную диаграмму).
7 Рассмотреть емкостный элемент цепи (дать определение ему, вывести формулу для ui при токе i=Imsinwt, показать их на графике, начертить векторную диаграмму).
8 Вывести формулу закон Ома для цепи переменного тока и раскрыть физическую сущность его, сопоставляя с формулой закона Ома для цепи постоянного тока.
9 Рассмотреть выражения 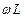 и
и 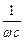 ; объяснить физическую сущность их и зависимость от частоты f. Постоянный ток, как частный случай переменного.
; объяснить физическую сущность их и зависимость от частоты f. Постоянный ток, как частный случай переменного.
10 Треугольники напряжений, сопротивлений, токов и проводимостей (получение треугольников, вывод аналитических выражений для комплекса полного напряжения, сопротивления, тока, проводимости в алгебраической, тригонометрической и показательной формах).
11 Средняя активная мощность (определение, вывод формулы). Коэффициент мощности (аналитическое выражение, определение; физическая сущность). Влияние коэффициента мощности на экономичность электропередачи.
12 Треугольники мощностей (получение треугольника, понятие об активной, реактивной и полной мощностях, единицы измерения их). Комплекс полной мощности в алгебраической, тригонометрической и показательной формах. Определение комплекса полной мощности через ток и напряжение. Комплекс полной мощности выраженной через ток и сопротивление.
13 Резонанс. Понятие о колебательной системе, собственной частоте колебаний в резонансах. Рассмотреть резонанс напряжений (схема, частотные характеристики, чем характерен, практическое значение).
14 Резонанс токов (в какой цепи возникает, при каких условиях, чем характерен, схема, частотные характеристики, практическое значение).








