3 Последовательное соединение активного, индуктивного и емкостного элементов (цепь R, L, C)

Дата: 2025-05-01; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Рассмотрим задачу расчета цепи, в которую входят последовательно соединенные все основные пассивные элементы (рисунок 3.14).

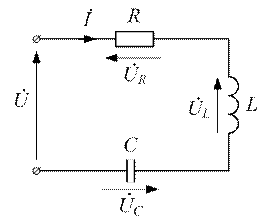
Рисунок 3.14 - Полная цепь переменного тока

Пусть требуется определить напряжения на элементах R, L, C, построить векторную диаграмму и найти ток, если заданы параметры цепи, угловая частота и общее входное напряжение цепи. Построить треугольник сопротивлений данной цепи и треугольник мощности.

Для построения векторной диаграммы произведем векторное сложение напряжений на всех элементах цепи

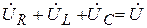. (3.19)

Это выражение является вторым законом Кирхгофа в векторной форме.

Построение диаграмм начинают с величины общей всех элементов цепи - с вектора тока .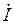

Вектор напряжения на активном сопротивлении совпадает по нап­рав­ле­нию с вектором тока, его называют активной составляющей напряжения, его величина равна:

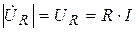. (3.20)

Вектор напряжения на катушке 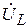опережает ток на угол 90°, его вели­чи­на равна:

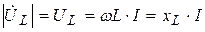. (3.21)

Вектор напряжения на конденсаторе отстает от тока на угол 90°, его величина равна:

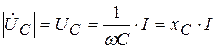. (3.22)

Векторная диаграмма при 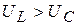Треугольник напряжений

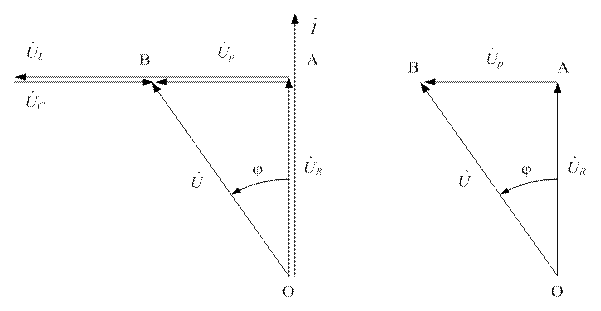
Рисунок 3.15 - Векторные диаграммы цепи RLC и треугольник напряжений

Замыкающий вектор, согласно (3.14), дает приложенное к цепи нап­ря­жение , оно сдвинуто по фазе относительно тока на угол .

При построении диаграммы условно принято, что 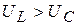. Такие цепи назы­ваются цепями с индуктивным режимом работы. Выделим на векторной диаграмме треугольник ОАВ, этот треугольник изображен отдельно и называется треугольником напряжений.

Вектор АВ называется реактивной составляющей напряжения

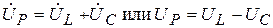
Из треугольника напряжений получим:

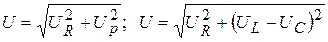. (3.23)

Для определения тока воспользуемся соотношениями (3.20), (3.21), (3.22) и подставим их в (3.23), тогда имеем

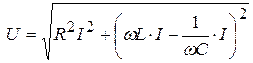, отсюда

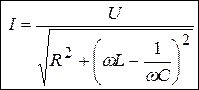или 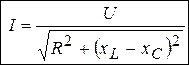(3.24)

Выражение (3.24) носит название закона Ома для полной цепи R, L, C.

Если все стороны треугольника напряжений ОАВ разделить на ток, получим треугольник сопротивлений. Гипотенуза этого треугольника соот­ветствует полному сопротивлению цепи - Z.

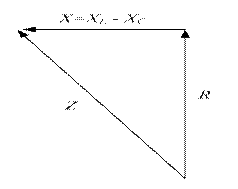
Рисунок 3.16 - Треугольник сопротивлений

Разность индуктивного и емкостного сопротивлений называется полным реактивным сопротивлением

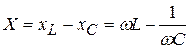. (3.25)

Из треугольника сопротивлений получаем соотношение

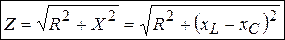, (3.26)

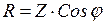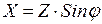; . (3.27)

С учетом (3.25) и (3.26) закон Ома примет вид

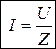. (3.28)

Умножая все стороны треугольника напряжений на ток цепи, получим треугольник мощности.

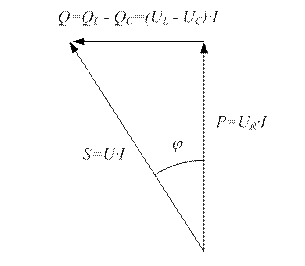
Рисунок 3.17 - Треугольник мощности

Разность реактивной индуктивной мощности и реактивной емкостной мощности называется реактивной мощностью, которая обозначается - Q. Эта мощность характеризует часть энергии, непрерывно циркулирующей в цепи и не совершающей полезной работы.

На рисунке 3.17:

Р - активная мощность, связанная с активными элементами, полностью преобразуемая в полезную работу;

S - полная или кажущая мощность цепи.

Из треугольника мощностей получим важные зависимости:

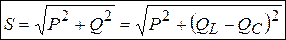, (3.29)

где

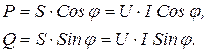(3.30)

Отношение активной мощности к полной, называется коэффициентом мощности

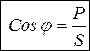. (3.31)

Коэффициент мощности зависит от соотношения активного и реактивных сопротивлений.

Задача № 5

Определить ток в цепи (рисунок 3.14) и напряжение на всех ее элементах, если , , , , .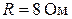

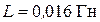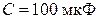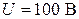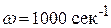Построить векторную диаграмму.

Решение

1. Определяем сопротивления элементов цепи:

индуктивное - ,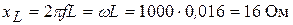

емкостное - 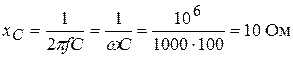, (3.32)

полное сопротивление –

.

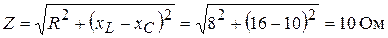2. Ток в цепи определяем по закону Ома для полной цепи переменного тока,

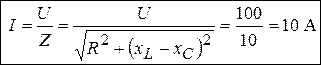. (3.33)

3. Напряжения на отдельных элементах цепи находим следующим образом:

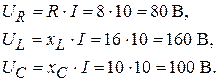(3.34)

3. Векторная диаграмма имеет вид, показанный на рисунке 3.15.