Анализируя выражение (3.9) и (3.12), видим, что напряжение на индуктивном элементе в любой момент времени опережает ток на угол, равный 90 ° .
2. Выражение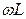 
(3.11) является реактивным индуктивным сопротивлением - 
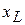реальной катушки,
.
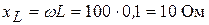3. Показание амперметра и вольтметра определяются как действующие значения
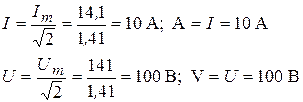
На рисунке 3.9 приведены графики изменения тока и напряжения, а также векторная диаграмма цепи.
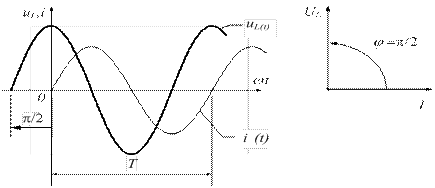
а) б)
а) графики функций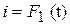 
, 
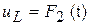; б) векторная диаграмма. Рисунок 3.9 - Ток и напряжение в цепи с индуктивностью
4 Запишем закон изменения мощности во времени
,
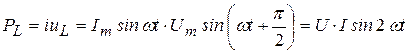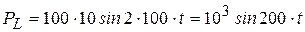. (3.13)
Из выражения (3.13) видим, что мощность в цепи с индуктивностью колеблется с двойной частотой, относительно частоты изменения тока и напряжения.
Представим закон изменения мощности графиком (рисунок 3. 10).
С энергетической точки зрения, такой характер графика мощности описывает накопление энергии в магнитном поле катушки и возврат ее обратно в источник энергии. Сечение проводов цепи в этом случае используется неэкономично, полезной работы в цепи не совершается. Мощность, характеризующая обмен энергии в цепи, называют - реактивной мощностью.
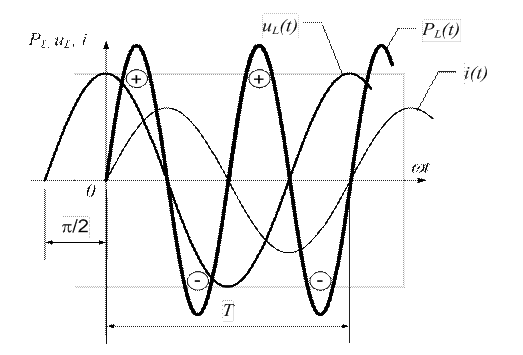
Рисунок 3.10 - График колебаний мощности на индуктивном элементе
Задача № 4
Записать закон изменения тока в цепи с идеальным конденсатором, найти действующие значения тока и напряжения, Определить показания приборов, если напряжение на входе цепи изменяется по закону
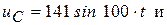
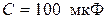
Построить векторную диаграмму и графики: ,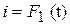 
, 
.
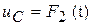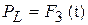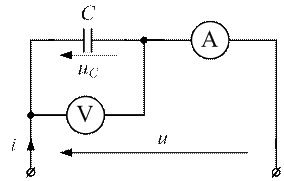
Рисунок 3.11 - Цепь с емкостным элементом
Решение
1. Идеальный конденсатор - элемент цепи, в котором электрическая энергия источника преобразуется в энергию электрического поля. Эта способность конденсатора характеризуется его параметром - емкостью С.
Если заряд на электродах конденсатора равен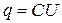 
(из курса физики), то через него протекает ток, который определяется как,
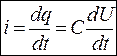. (3.14)
Отсюда видно, что причиной возникновения тока в конденсаторе является изменение напряжения на нем. Если напряжение не меняется, то ток через конденсатор равен нулю. Выражение (3.14) носит название закона Ома для диэлектрика конденсатора.
В нашем случае
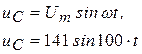(3.15)
Поэтому
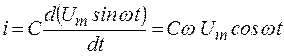
Переходя от косинуса к синусу, получаем
. (3.16)
Из выражения (3.16) следует, что
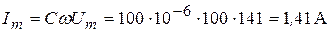
Значит мгновенное значение тока через конденсатор составит
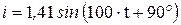. (3.17)
2. Из выражений (3.16) и (3.17) найдем действующие значения напряжения и тока, а также показания приборов, поскольку они показывают данные значения
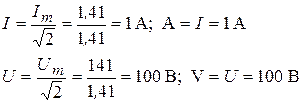
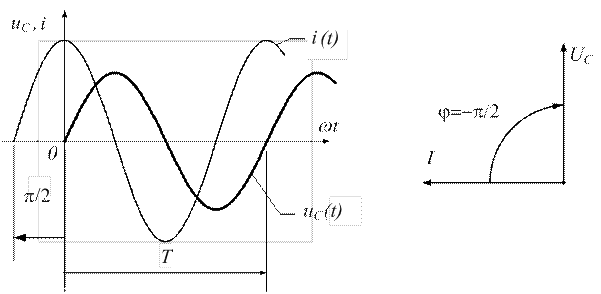
3. Сравнивая выражения (3.15) и (3.16), видим, что ток, протекающий через емкостной элемент в любой момент времени, опережает напряжение на угол, равный 90 °.
На рисунке 3.12 приведены графики: а) тока и напряжения на конденсаторе, б) векторная диаграмма тока и напряжения.
а) б)
а) графики тока и напряжения; б) векторная диаграмма тока и напряжения.
Рисунок 3.12 - Ток и напряжение на емкостном элементе:
Мгновенная мощность емкости
,
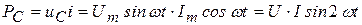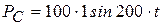. (3.18)
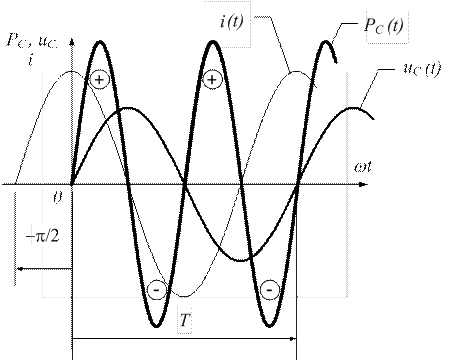
Рисунок 3.13 - График мгновенной мощности на емкостном элементе
Анализируя выражения (3.18), видим, что мгновенная мощность изменяется по синусоидальному закону с удвоенной частотой по сравнению с частотой тока и напряжения.
Сравнивая векторные диаграммы и графика колебаний мгновенных значений токов и напряжений на емкостном и индуктивном элементах, убеждаемся в противоположном действии на цепь емкости и индуктивности. Указанное свойство объясняет поведение электрических цепей в резонансных режимах.