Цепи переменного синусоидального однофазного тока
Вопросы теории и расчета цепей однофазного переменного тока рассмотрены далее на нескольких примерах решения типовых задач.
1 Способы изображения синусоидальных электрических величин
Задача № 1
Построить временную диаграмму, определить амплитудное, действующее и комплексное значения для напряжения, мгновенное значение которого изменяется по закону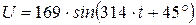 
.
Решение
1 Известно несколько способов представления величин, изменяющихся по синусоидальному закону, в виде:
· графиков изменения функций во времени,
· тригонометрических функций,
· вращающихся векторов,
· комплексных чисел.
В данной задаче напряжение задано тригонометрической функцией,
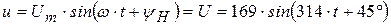(3.1)
где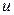 
- мгновенное значение напряжения или значение переменной величины в данный момент времени;
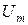- амплитудное значение напряжения;
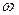- угловая частота;
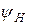- начальная фаза - угол, определяющий значение функции в начальный момент времени;
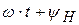- фаза колебания, характеризующая развитие процесса во времени.
Из выражения (3.1) имеем: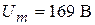 
; 
; 
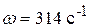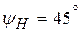, а также видно, что напряжение изменяется по закону синусоиды и может быть изображено графиком функции во времени (временной диаграммой).
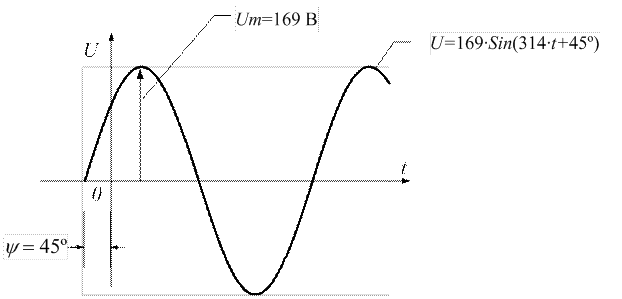
Рисунок 3.1 - Временная диаграмма напряжения
Действующее значение напряжения определим из соотношения
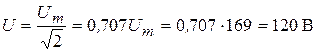. (3.2)
Среднее значение
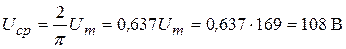. (3.3)
3. Известно, что вертикальная проекция вращающегося радиуса-вектора изменяется по закону синусоиды. Поэтому возможно обратное: синусоиду можно заменить радиусом-вектром, длина которого равна амплитуде (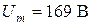 
), а скорость вращения - угловой скорости данной синусоидальной волны ( 
).
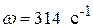Для момента времени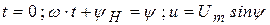 
, положение радиуса-вектора показано на рисунке 3.2.
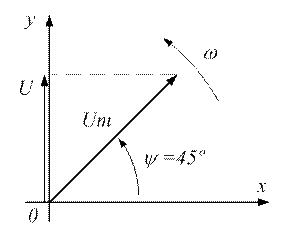
Рисунок 3.2 - Вектор напряжения
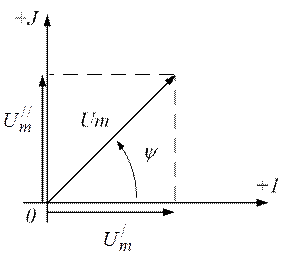
5. Поместим данный вектор в комплексную плоскость (рисунок 3.3).
| 
|
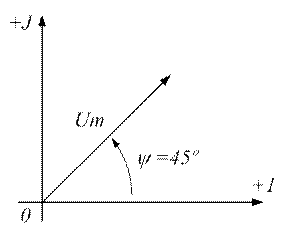
а) б)
Рисунок 3.3 - Вектор напряжения в комплексной плоскости (а) и его
проекция (б) на ос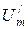и 
и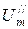 
.
Вектору напряжения в комплексной плоскости соответствует комплексное число, которое может быть записано в формах:
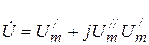- алгебраической,
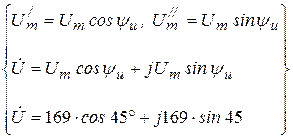- тригонометрической (3.4)
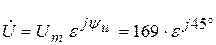- показательной.
2 Идеализированные элементы схем замещения цепей переменного тока
Задача № 2
Ток в цепи, содержащей резистор сопротивлением R=10 Ом (рисунок 3.3.), изменяется по закону
.
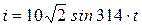Определить действующее значение тока и напряжения и записать закон изменения напряжения и мощности.
Построить векторную диаграмму и графики.
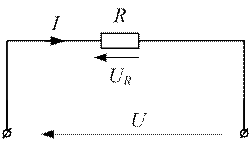
Рисунок 3.4 - Цепь с резистивным элементом
Решение
1. В идеальном резистивном (активном) элементе электрическая энергия источника полностью преобразуется в другие виды энергии. Сопротивление R - параметр резистора.
Из выражения,
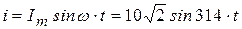(3.5)
амплитудное значение тока равно: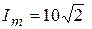 
А
Действующее значение тока равно: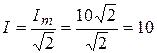 
А.
2. По закону Ома для действующих значений напряжение равно: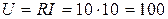 
В
По закону Ома мгновенных значений запишем выражение для мгновенного значения напряжения
; 
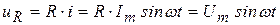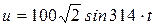. (3.6)
Сравнивая выражения (3.5) и (3.6) видим, что ток и напряжение в цепи с резистивным (активным) элементом в любой момент времени совпадают по фазе.
3. На рисунке 3.5 показаны графики зависимостей тока и напряжения в функции времени -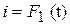 
, 
.
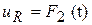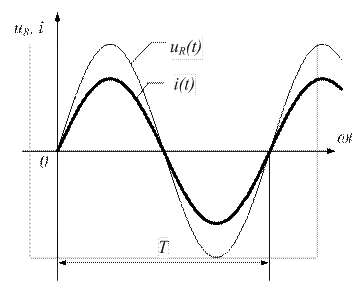
Рисунок 3.5 - Графики тока и напряжения на резистивном (активном) элементе
На векторных диаграммах для амплитудных и действующих значений тока и напряжения сдвиг фаз равен 0°. Отличие в построении этих диаграмм заключается в том, что длина всех векторов на диаграмме для действующих значений в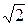 
раз меньше, чем длина соответствующих векторов на диаграмме для амплитудных значений.
Для амплитудных значений Для действующих значений
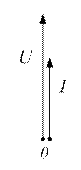
Рисунок 3.6 - Векторные диаграммы для резистивного (активного) элемента
3. Определим значение мощности в любой момент времени
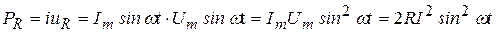
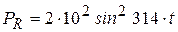. (3.7)
Из выражения (3.7) видим, что мощность в цепи с резистивным (активным) элементом всегда положительна, т.е. вся энергия источника питания цепи на резисторе полностью преобразуется в полезную (в данном случае - тепловую) работу. График колебания мощности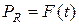 
приведен на рисунке 3.7.
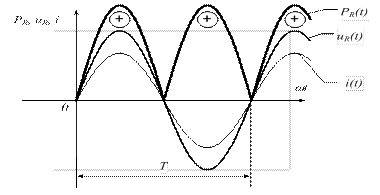
Рисунок 3.7 - График колебания мощности в цепи с идеальным резистивным элементом
Задача № 3
В цепи с индуктивным элементом (рисунок 3.8) ток изменяется по закону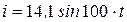 
, индуктивность катушки в цепи L= 0,1 Гн.
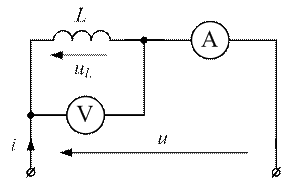
Рисунок 3.8 - Цепь с идеальным индуктивным элементом
Записать закон изменения напряжения и мощности, построить векторную диаграмму и графики ,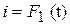 
, 
.
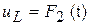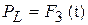Определить реактивное сопротивление цепи и показания приборов.
Решение
1. Идеальная индуктивная катушка - элемент цепи, в котором электрическая энергия источника преобразуется в энергию магнитного поля. Эта способность катушки характеризуется ее параметром - индуктивностью L.
Возникающая между концами катушки напряжение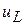 
идет на компенсацию ЭДС самоиндукции катушки 
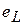, противодействующей прохождению тока. Поэтому закон изменения напряжения для данной цепи определяется так:
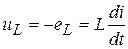, (3.8)
где
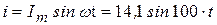; (3.9)
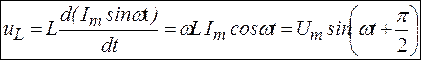. (3.10)
В выражении (3.10)
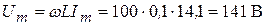(3.11)
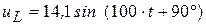. (3.12)