12 Законы гармонии систем
.Согласно Марутаеву М., исследователю гармонии в музыке и природе, законов гармонии три:
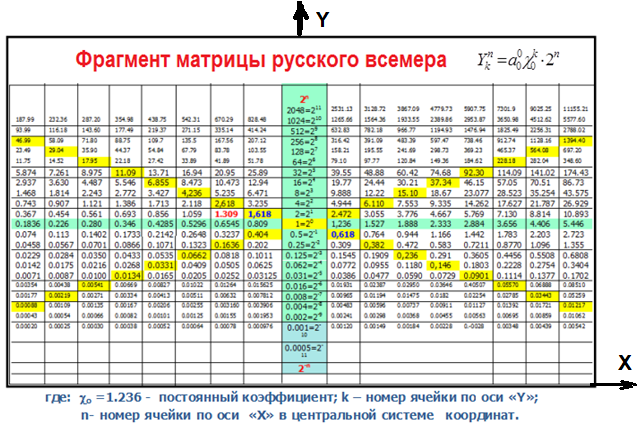
1- Закон качественной симметрии в матрице «Русского Всемера» отражен цифрами по оси Y: ниже «1» происходит деление части пополам, и отражает принцип дихотомии, т.е. зеркальной симметрия, эта пропорция есть сущность любой симметрии, например, зеркальной (угол падения равен углу отражения) – луч падающий и отраженный подобны и равны, а выше «1» - объединение частей в целое - удвоение (клетки делятся пополам и число их удваивается).
II - закон нарушенной симметрии. Закон нарушенной симметрии – его основой является среднее гармоническое равное квадрату среднегеометрического к среднеарифметическому Хгар = Хг2/Ха . Берется какой-то центр х k = 21/2 отсчета и относительно него симметрично 10 чисел, а затем эти 10 чисел делят на 11 равных частей неравномерно, но симметрично относительно его середины, т.е. темперируют диапазон. В итоге сдвиг относительно 21/2 задается числом a-10 = 25/11 = 1,370350985 – отклоняется от основного числа 21/2 = 1,41421…, т.е. фундаментальное число данного закона q = 0,9428 = 0,485/0,515 0 - число, выражающее нарушенную симметрию в границах октавы. Число q = 0,9428 связано с повторением исторических циклов, связанных с конкретными историческими личностями.
Пример 1. в мирное время существует постоянная соотношения рождаемости, средняя для всех рас. Это постоянная равна 106: на 100 девочек рождается 106 мальчиков – 100/106 = 0,485/0,515 =0,9417475 . Сдвиг на 6 мальчиков показывает на неоднородность появления детей разного пола.
Пример 2. Отмена крепостного права 1861 г. 19 февраля и ликвидация системы советов 1992 г., 4 октября. Общим для этих событий является освобождение. Берем отношение (с учетом месяцев и дней) 1860,136986/1992,756164 = 0,93344937.
 Пример 3. Французская революция 1789 г. и Октябрьская революция 1917 г. Берем отношение 1789/1917 = 0,9332…
Пример 3. Французская революция 1789 г. и Октябрьская революция 1917 г. Берем отношение 1789/1917 = 0,9332…
Строки матрица вдоль оси «Х» с иррациональными числами (где n -1…n) отражают закон нарушенной симметрии (примеры: музыка от Л.Бетховена до Г. Свиридова; расположение планет Солнечной системы; соотношение рожденных мальчиков и девочек в мирное время; и др.).
III - закон золотого сечения.
Вдоль диагоналей, параллельных оси «А-А» действует закон золотого сечения (примеров ему множество в окружающем мире – от архитектурных сооружений, человеческого тела до Вселенной).
Закон золотого сечения, он получен из законов I и II и отражает тождество отношения целого к его большей части и отношение большей части к меньшей. Выражается оно числами 1,618 или 0,618 = 1/1,618, что отражает неравное отношение частей системы, т.е. её неоднородность по конкретному параметру. Закон порождает числовые ряды в матрице Русского Всемера, являющейся матрицей всего живого и неживого в нашем мире.
В концепции Н.В. Левашова обращается внимание на то, что именно девять первичных материй образуют наиболее устойчивую систему метавселенных. Почему именно девять? При этом известно, что наиболее неустойчивыми образованиями, являются такие, которые синтезируются из двух и трёх форм материй.
Известно, что в природе все подчиняется законам гармонии (законам «золотого сечения», качественной симметрии и нарушенной симметрии), на которые современная наука не обращает внимание, очевидно считая их частностями. Поэтому предположим, что именно законы гармонии определяют порядок и последовательность образования суперпространств. Для этого вспомним как происходит образование шестилучевика, хотя известно масса примеров формирования космических структур по законам гармонии: расположение планет солнечной системы в пределах семи октав, спираль галактики «закручивается» по закону «золотого сечения» и др.
Конечно, эти законы являются следствием более общих законов мироздания, но они численно показывают, что мир наш устроен по законам гармонии.
Эти законы проявляются во всех явлениях мира: генетике, музыке, астрономии, физике, поэзии и т.д.
13.Основы гармонии мира
Наш мир гармоничен и это свойство самой развивающейся материи, устранять возникающие на её пути противоречия. Известны следующие типы гармонии: гармония формы, гармония покоя , гармония целесообразности и гармония минимально неделимого действия. Приведенные типы гармоний ранее представленные парными понятиями, т.е. в виде противоположностей, как отмечено выше, – «согласия» разногласных, т.к. всё сущее состоит из противоположностей, неразрывно связанных друг с другом, взаимоисключающих друг друга, а их противоречивое взаимодействие даёт импульс к развитию: Притяжение – отталкивание (пр.→о) - порождает гармонию минимально неделимых действий (Г1); Покой – движение (п→д)– порождает гармонию покоя (Г2,) как состояний объекта при его движении, т.е. как минимально неделимого движения; Форма – содержание (ф→с) - порождает гармонию формы (Г3), как наполнение её. целесообразностью при развитии объекта. Без взаимодействия противоположностей… покой-движение… не будет полной гармонии, только во взаимодействующих противоположностях она возможна (как в саморегулируемых, самонастраивающихся, самоуправляемых и т.п. системах) …
Взаимодействие и взаимосвязь гармоний условно можно представить в виде тетраэдра (рис. Г-2а.) или звездчатого тетраэдра (рис. Г-2б.), в вершинах которого находятся приведенные парные понятия, отражающие конструктивно суть гармонии, как проявление глубинной сути функционирования системы (рис. Г-2)
• Приведенные типы гармоний можно представить парными, как лица двуликого Януса, т. е. в виде противоположностей – «согласия» разногласных,
• т. к. всё существующее состоит из противоположностей, неразрывно связанных друг с другом, взаимоисключающих друг друга, а их противоречивое взаимодействие даёт импульс к развитию:
• Притяжение – отталкивание – порождает гармонию минимально неделимых действий;
Форма – содержание – порождает гармонию формы, ( Г3 ), как наполнение её минимально неделимым содержанием объектов любой мерной масштабности, и, наконец,
Целесообразность – иррациональность – порождает гармонию целесообразности;








