Теорема о изменении кинетической энергии системы
Задача 5
Теорема о изменении кинетической энергии системы
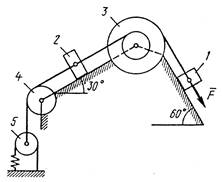
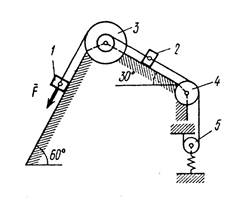
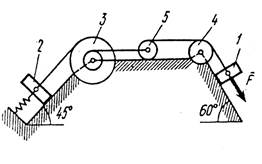
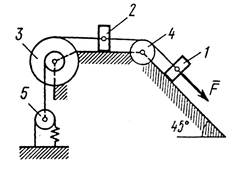
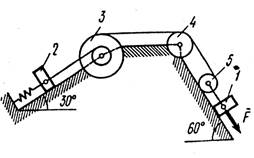
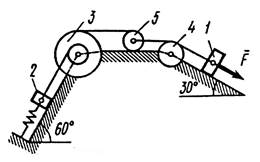
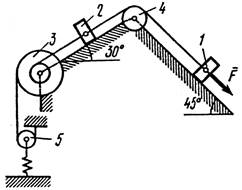
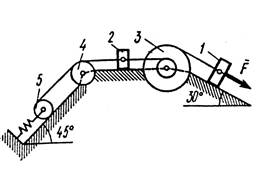
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 ( м) и r3 (м), а так же радиусом инерции относительно оси вращения ρ3 (м), блока 4 радиуса R4 (м) и катка (или подвижного блока) 5 (рис. 0 –9, табл. № 1); тело 5 считать сплошным однородным цилиндром, а массу блока 4 – равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 ( м). Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υ2, υ3 – скорости грузов 1, 2 и центра масс тела 5 соответственно, ω3 и ω4 – угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
Номер условия выбирается по четвертой цифре зачетки
Таблица № 1
| Номер условия | m1, кг | m2, кг | m3, кг | m4, кг | m5, кг | c, H/м | М, Н⋅м | F = f(s), H | Найти |
| 0 | 2 | 6 | 4 | 3 | 5 | 220 | 12 | 80(4 + 5s) | ω3 |
| 1 | 8 | 7 | 6 | 4 | 6 | 420 | 8 | 50(8 + 3s) | υ1 |
| 2 | 7 | 4 | 6 | 3 | 5 | 340 | 14 | 60(6 + 5s) | υ2 |
| 3 | 7 | 6 | 4 | 5 | 4 | 320 | 18 | 80(5 + 6s) | ω4 |
| 4 | 5 | 2 | 4 | 5 | 6 | 250 | 12 | 40(9 + 4s) | υ1 |
| 5 | 2 | 5 | 4 | 6 | 4 | 220 | 16 | 50(7 + 8s) | υC5 |
| 6 | 8 | 3 | 5 | 4 | 6 | 480 | 8 | 40(8 + 9s) | ω3 |
| 7 | 5 | 4 | 3 | 6 | 5 | 350 | 15 | 60(8 + 5s) | υ2 |
| 8 | 4 | 2 | 3 | 5 | 6 | 120 | 14 | 50(9 + 2s) | ω4 |
| 9 | 3 | 5 | 6 | 4 | 4 | 250 | 16 | 80(6 + 7s) | υC5 |
Номер чертежа выбирается по пятой цифре номера зачетки
| 
|
| Рис. 0 | Рис. 1 |
| 
|
| Рис. 2 | Рис. 3 |
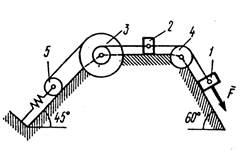
| 
|
| Рис. 4 | Рис. 5 |
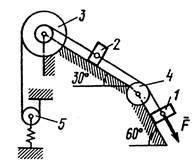
| 
|
| Рис. 6 | Рис. 7 |
| 
|
| Рис. 8 | Рис. 9 |
Значения величин таблицы №2 выбираются по пятой цифре варианта
Таблица № 2
| Номер варианта | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| R3 (м) | 0,3 | 0,5 | 0,65 | 0,4 | 0,8 | 0,7 | 0,9 | 0,45 | 0,85 | 0,35 |
| r3 (м) | 0,15 | 0,25 | 0,3 | 0,2 | 0,4 | 0,35 | 0,45 | 0,2 | 0,4 | 0,2 |
| ρ3 (м) | 0,1 | 0,5 | 0,2 | 0,5 | 0,2 | 0,2 | 0,3 | 0,1 | 0,2 | 0,3 |
| R4 (м) | 0,2 | 0,3 | 0,1 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 0,45 |
| f | 0,1 | 0,15 | 0,2 | 0,25 | 0,3 | 0,35 | 0,4 | 0,45 | 0,5 | 0,55 |
| s1 (м) | 0,3 | 0,2 | 0,1 | 0,4 | 0,5 | 0,35 | 0,25 | 0,15 | 0,45 | 0,55 |








