Расчетное задание 3. Работа с матрицами.
Задание 1. Написать функцию создания матрицы, элементы и размерность которой задаются по правилу, приведенному в таблице 1. В качестве входного аргумента функция получает размерность матрицы, N, выходной аргумент – сформированная матрица.
Задание 2. Написать функцию, которая вычисляет и выводит в командную строку следующие величины:
· определитель, след, ранг матрицы;
· числа обусловленности и нормы для матрицы: евклидову и L1;
· собственные числа и собственные вектора для полученной матрицы. Вывести матрицу собственных векторов и вектор собственных чисел.
· матрицы Q и R из QR-разложения
· матрицы L и U из LU- разложения матрицы.
В качестве входного аргумента функция получает матрицу, выходные аргументов у функции нет.
Задание 3. Написать функцию для решения СЛАУ вида Ax=b, считая, что b – единичный вектор:
· прямым вычислением;
· используя функцию linsolve;
· методом Гаусса.
· Используя матричное деление
И определяющую время работы каждой функции.
В качестве входного аргумента функция получает матрицу A, выходной аргумент –матрица размером N+1x4.Каждый столбец матрицы содержит время выполнения расчета (в первой строке) и решение.
Табл.1.
| № варианта | Правило создания матрицы А | Размерность матрицы А | № варианта | Правило создания матрицы А | Размерность матрицы А |
| 1 | 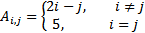
| 4 | 8 | 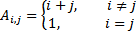
| 6 |
| 2 | 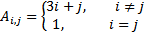
| 5 | 9 | 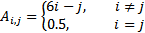
| 5 |
| 3 | 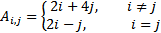
| 4 | 10 | 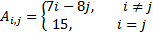
| 6 |
| 4 | 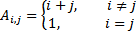
| 6 | 11 | 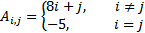
| 4 |
| 5 | 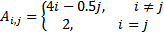
| 5 | 12 | 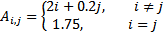
| 5 |
| 6 | 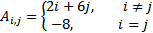
| 4 | 13 | 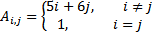
| 6 |
| 7 | 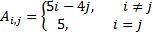
| 6 | 14 | 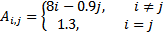
| 6 |
| 15 | 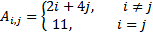
| 6 | 20 | 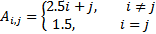
| 4 |
| 16 | 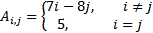
| 5 | 21 | 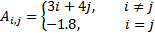
| 5 |
| 17 | 
| 4 | 22 | 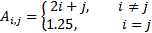
| 6 |
| 18 | 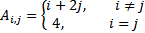
| 5 | 23 | 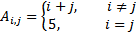
| 6 |
| 19 | 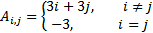
| 5 | 24 | 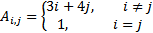
| 5 |








