<< < предыдущая 1 2 3 / 3 3

Вопросы и задания для самопроверки

Дата: 2025-05-01; Просмотры: 18

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

2.1. Выполните наглядное изображение, отображающее суть метода центрального проецирования. Подпишите элементы изображения.

2.2. Дайте определение центральной проекции точки.

2.3. Перечислите свойства центрального проецирования:

__________________________________________________________________ ____________________________________________________________________________________________________________________________________

__________________________________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

2.4. Выполните наглядное изображение, отображающее суть метода косоугольного параллельного проецирования. Подпишите элементы изображения.

2.5. Дайте определение параллельной проекции точки.

2.6. Перечислите свойства параллельного проецирования:

__________________________________________________________________ ____________________________________________________________________________________________________________________________________

2.7. Выполните наглядное изображение, отображающее суть метода прямоугольного (ортогонального) параллельного проецирования. Подпишите элементы изображения.

2.8. Чем различаются методы косоугольного и прямоугольного (ортогонального) параллельного проецирования?

__________________________________________________________________ ____________________________________________________________________________________________________________________________________

__________________________________________________________________

2.9. Какой метод проецирования является основным в “Начертательной геометрии” и почему?

__________________________________________________________________ ____________________________________________________________________________________________________________________________________

3. ПРОЕКЦИИ ТОЧКИ

Вопросы и задания для самопроверки

3.1. Сколько проекций точки определяют ее положение в пространстве? ______________________________________________________________________________________________________________________________________________________________________________________________________

3.2. В чем заключается суть проецирования по Монжу? _____________

3.3. Выполните наглядное изображение, отображающее метод проецирования на две взаимно перпендикулярные плоскости проекций. Покажите на нем, как происходит преобразование пространственной модели проецирования в плоскую модель. Подпишите элементы изображения.

3.4. Вычертите эпюр Монжа для произвольной пространственной точки. Подпишите элементы эпюра.

3.5. Что является проекцией точки на плоскость? ___________________

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

3.6. Какими свойствами обладает эпюр? __________________________

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

3.7. Что значит “прочитать эпюр”? _______________________________

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

3.8. Выполните наглядное изображение, отображающее метод проецирования на три взаимно перпендикулярные плоскости проекций. Покажите на нем, как происходит преобразование пространственной модели проецирования в плоскую модель. Подпишите элементы изображения.

3.9. Вычертите комплексный чертеж произвольной пространственной точки. Подпишите элементы чертежа.

3.10. Что такое “координаты точки”, как они обозначаются и определяются? _____________________________________________________

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

3.11. Постройте три проекции точки А (20,25,30) (координаты указаны в мм). Запишите комбинации координат, по которым строятся горизонтальная, фронтальная и профильная проекции точки.

3.12. Достройте третью (профильную) проекцию точки по двум имеющимся. Перечислите способы построения.

4. ПРОЕКЦИИ ПРЯМОЙ

Вопросы и задания для самопроверки

4.1. Вычертите проекции прямой общего положения. Дополните чертеж проекциями точек, принадлежащих и не принадлежащих построенной прямой.

4.2. Дайте определение прямых частного положения и постройте их эпюры.

Прямые уровня – это __________________________________________ ____________________________________________________________________________________________________________________________________

Проецирующие прямые – это ___________________________________ ____________________________________________________________________________________________________________________________________

4.3. Что является следом прямой? Вычертите проекции прямой общего положения и постройте ее фронтальный и горизонтальный следы.

4.4. Вычертите проекции прямой общего положения и разделите ее в отношении 3:7.

4.5. Вычертите проекции прямой общего положения и определите ее натуральную величину и углы наклона ее к плоскостям проекций методом прямоугольного треугольника.

4.6. Дайте определение параллельных, пересекающихся, скрещивающихся прямых и вычертите их проекции.

Параллельные прямые – это ____________________________________ ____________________________________________________________________________________________________________________________________

Пересекающиеся прямые – это __________________________________ ____________________________________________________________________________________________________________________________________

__________________________________________________________________

Скрещивающиеся прямые – это _________________________________ ____________________________________________________________________________________________________________________________________

__________________________________________________________________

4.7. Какие точки называются конкурирующими? Приведите правило определения видимости геометрических элементов по конкурирующим точкам и проиллюстрируйте его эпюром.

Конкурирующие точки – это ___________________________________ ____________________________________________________________________________________________________________________________________

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

4.8. Приведите теорему Монжа о проецировании прямого угла. Проиллюстрируйте определение эпюром.

Теорема Монжа. ______________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

5. ПРОЕКЦИИ ПЛОСКОСТИ

Вопросы и задания для самопроверки

5.1. Перечислите способы задания плоскости на чертеже и проиллюстрируйте их эпюрами.

Плоскость на чертеже может задаваться следующими способами:

1) ___________________________________________________________

2) ___________________________________________________________ __________________________________________________________________

3) ___________________________________________________________ __________________________________________________________________

4) ___________________________________________________________ __________________________________________________________________

5) ___________________________________________________________ __________________________________________________________________

6) ___________________________________________________________ __________________________________________________________________

7) ___________________________________________________________ __________________________________________________________________

5.2. Дайте определение плоскости общего положения.

Плоскость общего положения – это _____________________________ ______________________________________________________________________________________________________________________________________________________________________________________________________

5.3. Что такое следы плоскости? Вычертите эпюры плоскостей, заданных следами.

Следы плоскости – это ________________________________________ ______________________________________________________________________________________________________________________________________________________________________________________________________

5.4. Дайте определение плоскостей частного положения и постройте их эпюры.

Плоскости уровня – это ________________________________________ ____________________________________________________________________________________________________________________________________

Проецирующие плоскости – это ________________________________ ____________________________________________________________________________________________________________________________________

5.5. Сформулируйте условия принадлежности прямой и точки плоскости.

Прямая принадлежит плоскости, если _________________________ ______________________________________________________________________________________________________________________________________________________________________________________________________

Точка принадлежит плоскости, если ___________________________ ______________________________________________________________________________________________________________________________________________________________________________________________________

5.6. Приведите эпюры решения основных задач.

5.6.1. Достройте недостающую проекцию прямой: 1) по двум точкам пересечения ее с определителем; 2) по одной точке и признаку параллельности.

5.6.2. Достройте недостающую проекцию точки двумя способами.

5.7. Дайте определение прямых, занимающих особое положение в плоскости (главных линий плоскости) – горизонталей, фронталей, профильных прямых и линий ската. Проиллюстрируйте определения соответствующими эпюрами. Для чего используются и как строятся линии ската плоскостей?

Горизонтали – это ____________________________________________ ______________________________________________________________________________________________________________________________________________________________________________________________________

Фронтали – это _______________________________________________ ______________________________________________________________________________________________________________________________________________________________________________________________________

Профильные прямые – _________________________________________ ____________________________________________________________________________________________________________________________________

Линии наибольшего наклона плоскости к плоскостям проекций (линии ската) – это ________________________________________________ ______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

5.8. Перечислите случаи взаимного расположения плоскостей. Каким образом определяется взаимное положение плоскостей? __________________

1)_________________________________________________________________2)_________________________________________________________________3)_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

5.9. Дайте определение параллельных плоскостей и приведите примеры изображения таких плоскостей на чертеже.

Параллельные плоскости ______________________________________

____________________________________________________________________________________________________________________________________

5.10. Дайте определение пересекающихся плоскостей.

Пересекающиеся плоскости ___________________________________

____________________________________________________________________________________________________________________________________

5.11. Как строится линия пересечения двух плоскостей? Рассмотрите два случая – частный и общий.

Частный случай пересечения двух плоскостей рассматривается, когда

____________________________________________________________________________________________________________________________________

Линия пересечения в этом случае строится ________________________

____________________________________________________________________________________________________________________________________

Общий случай пересечения двух плоскостей рассматривается, когда

____________________________________________________________________________________________________________________________________

Порядок определения линии пересечения в этом случае:

1) ___________________________________________________________ ____________________________________________________________________________________________________________________________________

2) ___________________________________________________________ ____________________________________________________________________________________________________________________________________

3) ___________________________________________________________ ____________________________________________________________________________________________________________________________________

4) ___________________________________________________________ ____________________________________________________________________________________________________________________________________

5.12. Перечислите случаи взаимного расположения прямой и плоскости.

5.13. В каких случаях прямая считается параллельной плоскости? Проиллюстрируйте чертежом.

1)_____________________________________________________________________________________________________________________________________________________________________________________________________

2)_____________________________________________________________________________________________________________________________________________________________________________________________________

5.14. Как строится точка пересечения прямой и плоскости? Рассмотрите два случая – частный и общий.

Частный случай пересечения прямой и плоскости рассматривается, когда__________________________________________________________________________________________________________________________________________________________________________________________________

Точка пересечения в этом случае строится ________________________

____________________________________________________________________________________________________________________________________

Общий случай пересечения прямой и плоскости рассматривается, когда__________________________________________________________________________________________________________________________________________________________________________________________________

Порядок определения линии пересечения в этом случае:

1) ___________________________________________________________ ____________________________________________________________________________________________________________________________________

2) ___________________________________________________________ ____________________________________________________________________________________________________________________________________

3) ___________________________________________________________ ____________________________________________________________________________________________________________________________________

4) ___________________________________________________________

5.15. Какая прямая считается перпендикулярной плоскости и как она строится? Проиллюстрируйте ответ соответствующим чертежом.

Прямая перпендикулярна плоскости, если _______________________ ____________________________________________________________________________________________________________________________________

В качестве таких прямых удобно рассматривать ________________ __________________________________________________________________

__________________________________________________________________

______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

5.16. Какие плоскости считаются взаимно-перпендикулярными? Проиллюстрируйте ответ соответствующим чертежом.

__________________________________________________________________

______________________________________________________________________________________________________________________________________________________________________________________________________

6. ЗАДАЧИ ПО ТЕМАМ “ПРОЕКЦИИ ТОЧКИ, ПРЯМОЙ, ПЛОСКОСТИ”

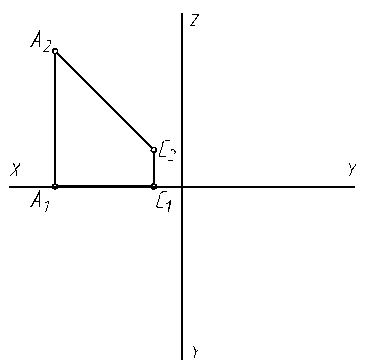
6.1. Постройте проекции треугольника АВС, если даны координаты его вершин А (20,0,0), В (0,30,0), С (0,0,25).

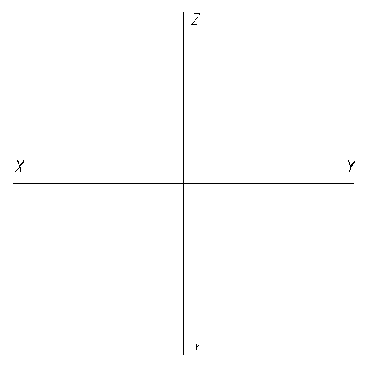
6.2. Постройте проекции треугольника АВС, если даны координаты его вершин А (20,30,0), В (20,0,30), С (0,20,30).

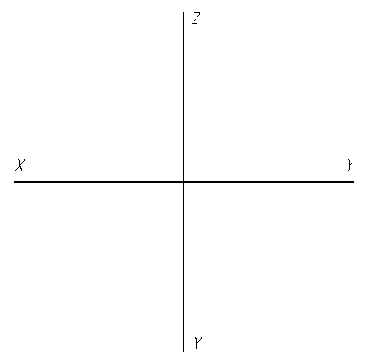
6.3. Постройте проекции куба с основанием АВС D на фронтальной плоскости проекций, если дана диагональ АС его основания. Указать проекции каждой грани и каждого ребра.

6.4. Постройте проекции прямого кругового цилиндра с основанием на фронтальной плоскости проекций и с центром О (30,0,30), если его высота равна 60 мм, а радиус основания равен 20 мм.

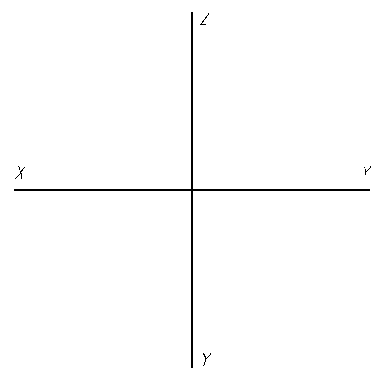
6.5. На прямой CD отложить отрезок, равный l.

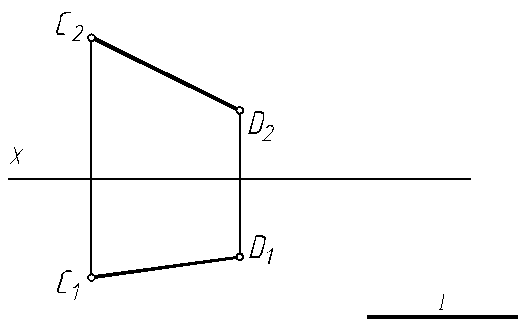
6.6. Постройте равнобедренный треугольник с основанием АВ и вершиной, расположенной на прямой CD.

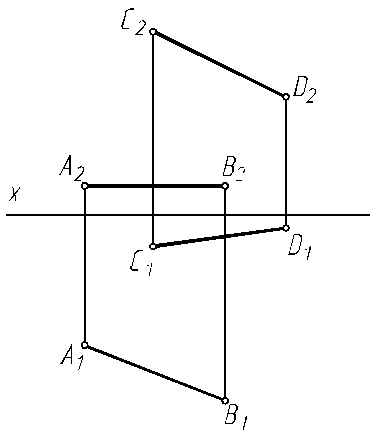
6.7. Достройте недостающую проекцию пятиугольника ABCDE.

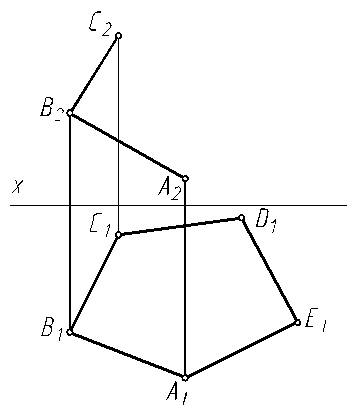
6.8. Постройте следы плоскости, заданной двумя пересекающимися прямыми АВ и АС.

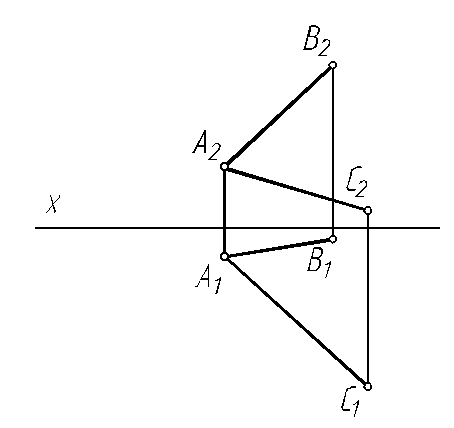
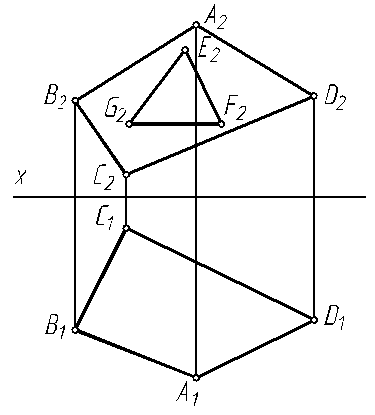
6.9. Построить горизонтальную проекцию треугольника GEF, принадлежащего плоскости четырехугольника АВС D.

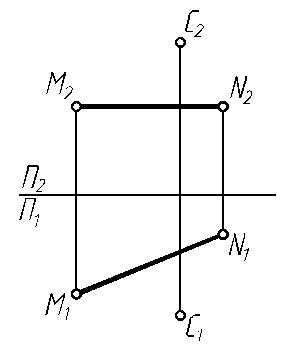
6.10. Построить проекции квадрата ABCD со стороной АВ, расположенной на прямой MN.

6.11. Построить горизонтальную проекцию треугольника АВС, принадлежащего плоскости Р.

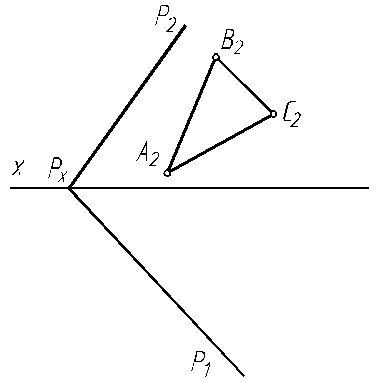
6.12. Через точку М проведите прямую, параллельную плоскости треугольника АВС и горизонтальной плоскости проекций.

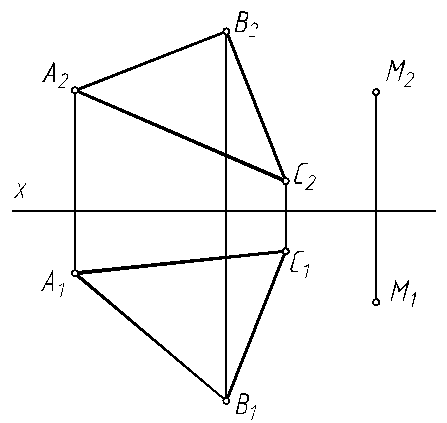
6.13. Через прямую АВ проведите плоскость, параллельную прямой CD.

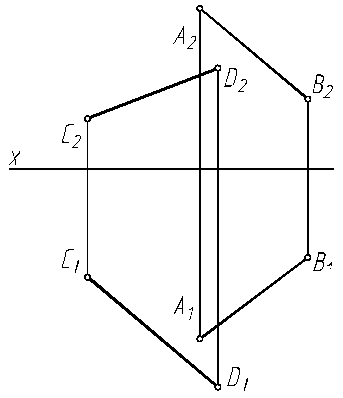
6.14. Определите параллельны ли плоскости АВ C и MNL.

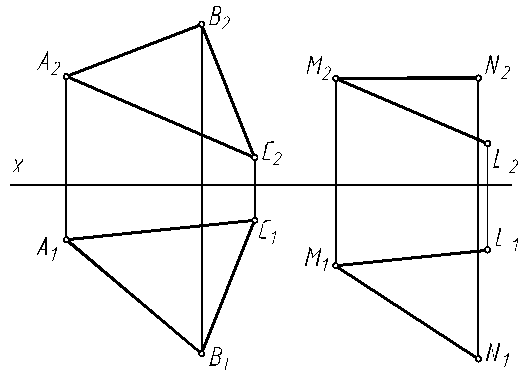
6.15. Построить линию пересечения треугольников АВС и DEF. Определить видимость пересекающихся элементов.

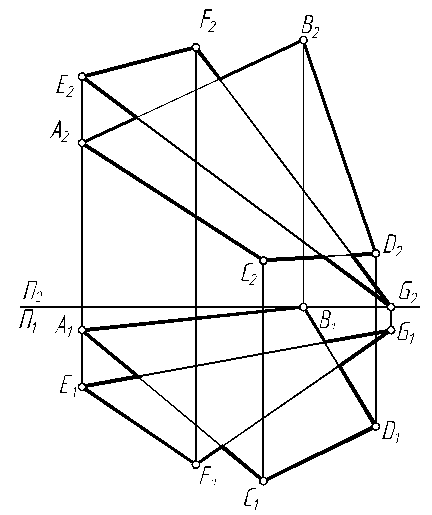
6.16. Построить линию пересечения двух плоскостей Р и Г, заданных следами.

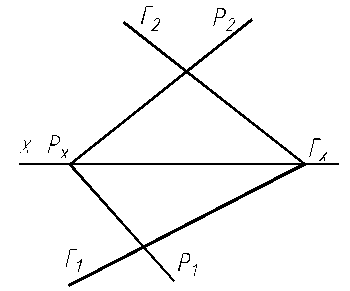
6.17. Построить линию пересечения двух плоскостей Р и Г, заданных следами.

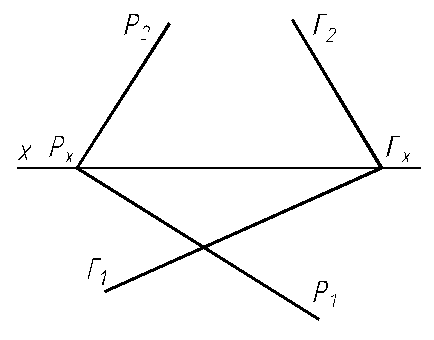
6.18. Построить линию пересечения треугольника АВС и плоскости Р, заданной следами.

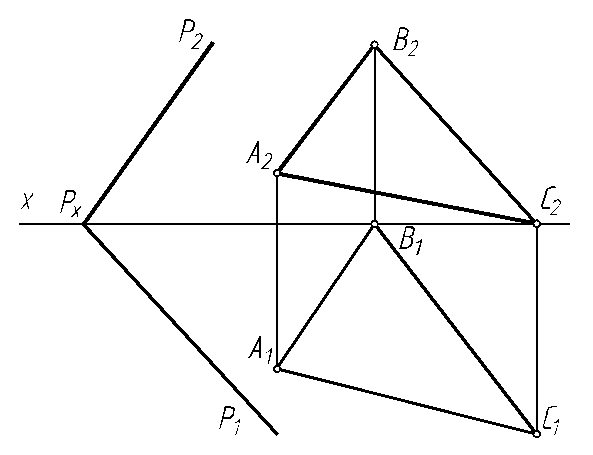
6.19. Найти точку пересечения прямой DE с плоскостью треугольника АВС. Определите видимость прямой относительно треугольника.

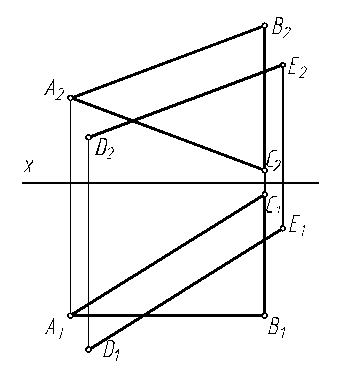
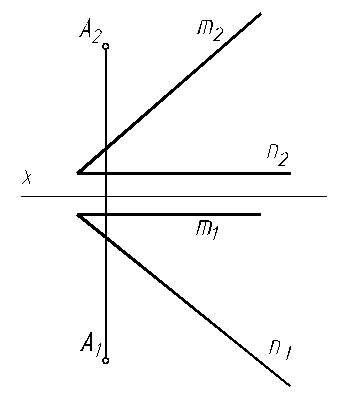
6.20. Найти точку пересечения прямой l с плоскостью, заданной двумя параллельными прямыми m и n.

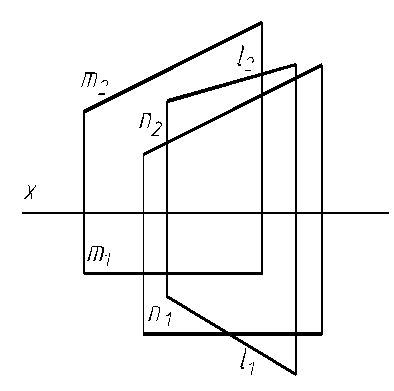
6.21. Найдите точку пересечения прямой l с плоскостью Р, заданной следами.

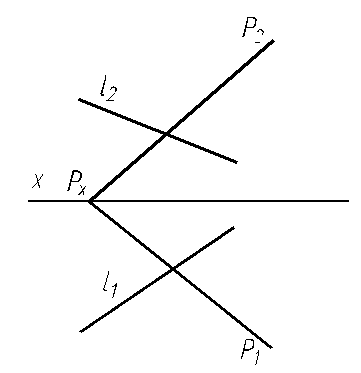
6.22. Определите расстояние от точки А до плоскости Р, заданной следами.

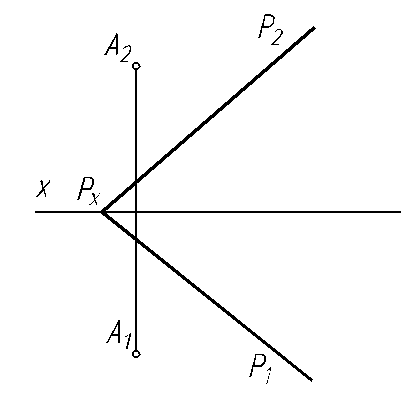
6.23. Постройте точку пересечения горизонтально-проецирующей прямой АВ с плоскостью Р, заданной следами.

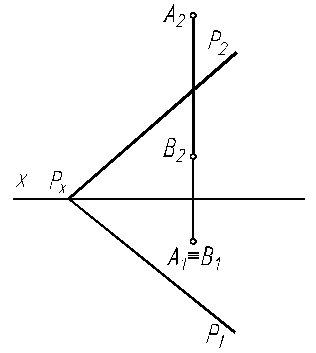
6.24. Определите расстояние от точки А до плоскости, заданной двумя пересекающимися прямыми m и n.

<< < предыдущая 1 2 3 / 3 3