Исследование рядов на сходимость с помощью MathCAD . Приближенные вычисления с помощью рядов с использованием MathCAD и Excel
1. Цель работы
1.1.Научиться вычислять члены числового ряда с помощью пакета MathCAD;
1.2 Научиться исследовать числовые ряды на сходимость с помощью пакета MathCAD;
1.3 Научиться раскладывать функции в ряды Тейлора и Маклорена с помощью пакета MathCAD
1.4 Научиться применять ряды для приближённых вычислений значений функций
1.5 Научиться применять ряды для приближённых вычислений значений определённых интегралов
2. Оборудование
Пакет программ MathCAD
3. Ход работы
3.1 Вариант
1. Рассматривая частичные суммы, исследовать ряд на сходимость с помощью пакета Mathcad:
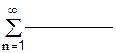
2. Проверить с помощью пакета Mathcad выполнение необходимого признака сходимости у ряда:
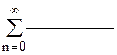
3. Исследовать ряд на сходимость с помощью пакета Mathcad: 
4. Исследовать на сходимость знакочередующийся ряд помощью пакета Mathcad. Если ряд сходится, то определить сходится он абсолютно или условно:
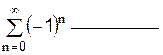
5. Разложить функцию в ряд по степеням х помощью пакета Mathcad:
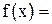
6. Разложить многочлен в ряд по степеням (х ) помощью пакета Mathcad:
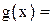
7. С помощью MS Excel вычислите
1) первые двадцать членов ряда 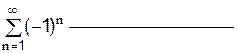 ;
;
2) найдите их модули;
3) оцените погрешность, допускаемую при замене суммы ряда суммой первых его пяти членов;
4) найдите сумму членов ряда с точностью 0,01;
5) найдите сумму членов ряда с точностью 0,001;
8. Для функции y(x) =
1) Вычислите точное значение при х = ;
2) Разложите функцию в степенной ряд;
3) Замените функцию суммой первых пяти членов ряда;
4) Найдите приближённое значение функции при данном значении х;
5) Вычислите абсолютную и относительную погрешность этого приближения;
6) Постройте в одной системе координат график функции и суммы первых пяти членов ряда
9. Для интеграла 
1) Вычислите точное значение;
2) Разложите подынтегральную функцию в степенной ряд;
3) Замените подынтегральную функцию суммой первых пяти членов ряда;
4) Проинтегрируйте полученное выражение;
5) Найдите приближённое значение интеграла, вычислив значение полученной функции при х равном верхнему пределу интегрирования;
6) Вычислите абсолютную и относительную погрешность этого приближения;
10. С помощью степенного ряда вычислить значение функции y(x) = , при х = с точностью ε = 0,001.
 3.2 Допуск к работе
3.2 Допуск к работе
3.2.1 На какой панели в пакете Mathcad находятся знаки суммы и бесконечности?
_____________________________________________________________________________________
3.2.2 Сделайте вывод о сходимости числового ряда, на основании исследования его частичных сумм:.
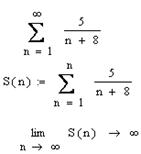
_____________________________________________________________________________________
3.2.3 Сделайте вывод о выполнении необходимого условия сходимости ряда:

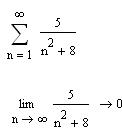
_____________________________________________________________________________________
3.2.4 С каким рядом надо сравнить ряд 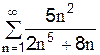 для исследования его на сходимость с использованием предельного признака сходимости?
для исследования его на сходимость с использованием предельного признака сходимости?
_____________________________________________________________________________________
3.2.5 Сделайте вывод о сходимости ряда, исследуемого по признаку Коши
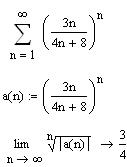
3.2.6 Сделайте вывод о сходимости ряда, исследуемого по признаку Даламбера
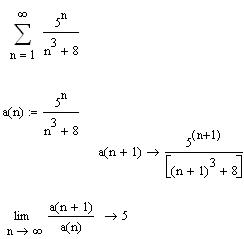
_____________________________________________________________________________________
3.2.7 Сделайте вывод о сходимости знакочередующегося ряда:

_____________________________________________________________________________________
 3.2.8 Укажите интервал сходимости степенного ряда:
3.2.8 Укажите интервал сходимости степенного ряда:
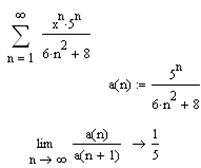
_____________________________________________________________________________________
3.2.9 Заполните пропуски:
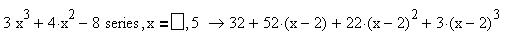
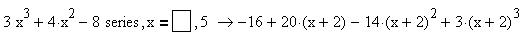
3.2.10 Заполните ячейки В2 и С2 формулами, для вычисления первых членов и их модулей для ряда: 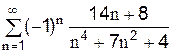
3.2.11 Записаны первые пять членов ряда
| а1 | а2 | а3 | а4 | а5 | а6 | а7 |
| 0,17 | 0,13 | 0,12 | 0,11 | 0,09 | 0,05 | 0,007 |
А) Сколько членов ряда надо взять, чтобы вычислить его сумму с точностью 0,1 ____________
Б) Сколько членов ряда надо взять, чтобы вычислить его сумму с точностью 0,01 ___________
В) Какова будет погрешность, если сумму ряда заменить суммой первых его трёх членов _____
3.2.12 Точное значение 0,357, а приближённое 0,361 Вычислите абсолютную погрешность
____________________________________________________________________________________
3.2.13 Точное значение 0,357, а приближённое 0,361. Запишите формулу для вычисления относительной погрешности
____________________________________________________________________________________
К работе допускается ______________
4. Результаты работы
1)
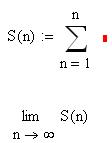
Вывод: ____________________________________________________________________________
2)
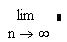
Вывод: ____________________________________________________________________________
3) a(n)=
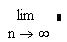
Вывод: ряд _________________________________ по признаку _____________________________
 |
4)

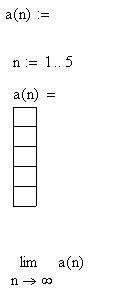
ряд _________________________________ по признаку _____________________________
ряд из модулей 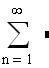
по признаку __________________________________________________________________т.к
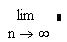
Вывод: _________________________________________________________________________
5)
_____________________________________________________________________________________
6)
_____________________________________________________________________________________
7)
| n | an | модуль an |
1) погрешность, допускаемую при замене суммы ряда суммой первых его пяти членов;
_____________________________________________
2) сумма членов ряда с точностью 0,01;
______________________________________________
3) сумма членов ряда с точностью 0,001;
______________________________________________
|
| 1 |
|
| |
| 2 |
|
| |
| 3 |
|
| |
| 4 |
|
| |
| 5 |
|
| |
| 6 |
|
| |
| 7 |
|
| |
| 8 |
|
| |
| 9 |
|
| |
| 10 |
|
| |
| 11 |
|
| |
| 12 |
|
| |
| 13 |
|
| |
| 14 |
|
| |
| 15 |
|
| |
| 16 |
|
| |
| 17 |
|
| |
| 18 |
|
| |
| 19 |
|
| |
| 20 |
|
|
 8) y(x) =
8) y(x) =
y(x),series,___ ,_____ →
g(x)=
x=
точное значение у( _____ ) =
приближённое значение g( ____ ) =
абсолютная погрешность ______
относительная погрешность ________
9) Точное значение  =
=
Подынтегральная функция g(x) =
Разложение подынтегральной функции в степенной ряд
_g(x) series, _______, →_____________________________________________________
Интеграл от полученного степенного ряда
__________________________________________________________________________
Приближённое значение интеграла
абсолютная погрешность ______
относительная погрешность ________
10)
y(x) =
y(x),series,___ ,_____ →
члены ряда
| а1 | а2 | а3 | а4 | а5 | а6 | а7 | а8 | а9 |
|
|
|
|
|
|
|
|
x=
точное значение у( _____ ) =
приближённое значение

5. Вывод
В ходе выполнения данной работы _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________
 |
ПРАКТИЧЕСКАЯ РАБОТА 18








