Решение дифференциальных уравнений в Mathcad

Дата: 2025-05-01; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

1. Цель работы

Научиться находить с помощью пакета MathCAD общие и частные решения дифференциальных уравнений первого и второго порядка, используя правила решения дифференциальных уравнений и встроенные функции пакета MathCAD.

2. Оборудование

Пакет программ MathCAD.

3. Ход работы

3.1 Вариант

1. Найти общее решение данного дифференциального уравнения

1. Найти общее решение данного дифференциального уравнения

1. Найти общее решение дифференциального уравнения и выполнить проверку

1. Известно, что тело движется с ускорением a(t) = _______________________________,

найти закон изменения скорости и закон движения тела, если

при t = 0, S = _________ , v = ______________

1. Решите дифференциальное уравнение, используя блок given, odesolve

на отрезке [ ; ], разбив его на ______ частей, если у( ) =

1. Решите дифференциальное уравнение, используя команду rkfixed

на отрезке [ ; ], разбив его на ______ частей, если у( ) =

1. Решите дифференциальное уравнение, используя блок given, odesolve

на отрезке [ ; ], разбив его на ______ частей, если у( ) =

Постройте в одной системе координат график приближённого и точного аналитического решения у =

3.2. Допуск к работе

4.2.1. Разделите переменные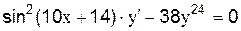

____________________________________________________________________________________________________________________________________________________________

____________________________________________________________________________________________________________________________________________________________

4.2.2. Комбинацией каких клавиш вызывается в документе MathCAD команда символьных операций (→) ?

____________________________________________________________________________________________________________________________________________________________

4.2.3. Пусть y’ = z , тогда y ” = ?

4.2.4. Известно, что S(t) = 15t² + 4t + C и при t = 2, S = 10. Найти С

____________________________________________________________________________________________________________________________________________________________

4.2.5. Продолжите равенства a(t) = v ‘ (t) =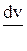

v (t) = S ‘ (t) =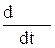

4.2.6. Известно, что отрезок [2;3] разбили на 10 частей продолжите ряд

2; _______________________________________________________________

4.2.7. Известно, что отрезок [4;7] разбили на 6 частей продолжите ряд

2; _______________________________________________________________

4.2.8. Комбинацией каких клавиш MathCAD вызывается знак «жирного» равенства?

____________________________________________________________________________________________________________________________________________________________

4.2.9. Как на панели матриц выглядит клавиша для вывода на экран двоеточия в MathCAD (2 .. 3)?

____________________________________________________________________________________________________________________________________________________________

4.2.10 С помощью какой закладки мастера форматирования графиков можно

изменить внешний вид линии графика ( например сделать его точечным)?

____________________________________________________________________________________________________________________________________________________________

К работе допускается ______________

4. Результаты работы

1.

2.

dy(x,C1) =

y(x,C1,C2) =

3. Характеристическое уравнение:

Корни характеристического уравнения: k₁ = k₂ =

Общее решение уравнения:

Поверка правильности решения: (запись с экрана)

4.

v(t,C1) =

C1 =

S(t,C1,C2) =

C2 =

S(t,C1,C2) =

5.

given

___________________ = ________________

y( ) = ____

y := odesolve (x,___ , _____)

x:= ____ , ______ .. ____

x = y(x)=

6.

y:=

F(x,y):=

y1:=rkfixced(y,___ , ____ , ____, F

y1=

7.

given

___________________ = ________________

y( ) = ____

y := odesolve (x,___ , _____)

x:= ____ , ______ .. ____

x = y(x)=

h(x): =

5. Вывод

В ходе выполнения данной работы _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________

ПРАКТИЧЕСКАЯ РАБОТА 16

Числовые и степенные ряды.

1. Цель работы

1.1.Научиться вычислять члены числового ряда и исследовать числовые ряды на сходимость

1.2 Научиться раскладывать функции в ряды Тейлора и Маклорена

2. Ход работы

2.1 Вариант

1.Найдите первые три члена ряда : .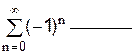

2.Определить сходится или расходится данный геометрический ряд :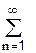

3.Определить сходится или расходится данный гармонический ряд :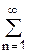

4.Выполняется ли необходимый признак сходимости у ряда :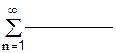

5.С помощью предельного признака исследовать ряд :