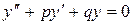Решение дифференциальных уравнений второго порядка
1. Цель работы
1.1 Научиться решать дифференциальные уравнения второго порядка, допускающие понижение порядка.
1.2 Научиться решать линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
1.3 Научиться применять дифференциальные уравнения к решению физических задач
2. Ход работы
2.1 Вариант
Найдите общее решение дифференциального уравнения:
1) _____________________________________________
2) ______________________________________________
Найдите частное решение дифференциального уравнения:
3) ______________________________________________
______________________________________________
4) _______________________________________________________________________________
Найдите закон движения точки:
5) _______________________________________________________________________________
6)________________________________________________________________________________
2.2 Допуск к работе
2.2.1 Решите уравнение 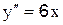
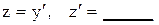
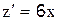
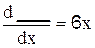
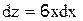
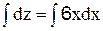






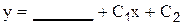
2.2.2 Вычислите 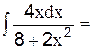
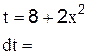
2.2.3 Продолжите равенства: a) ln 5 + ln 4 = ln 5∙4 = ln _____
б) ln(x+3) + lnC = _____________________
в) ln 12 = b ↔ 12 = e b
г) ln z = 5x + 8 ↔ z = 
д) 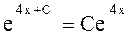
е) 
2.2.4 Заполните таблицу:
| Дифференциаль- ное уравнение |
| ||
| Характеристичес- кое уравнение |
| ||
| Дискриминант |
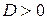
|
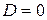
|
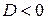
|
| Корни характеристичес-кого уравнения | |||
| Общее решение дифференциаль- ного уравнения | |||
К работе допускается ______________
4. Результаты работы
 ПРАКТИЧЕСКАЯ РАБОТА 14
ПРАКТИЧЕСКАЯ РАБОТА 14
Применение дифференциальных уравнений для решения прикладных задач
1. Цель работы
1.1 Научиться применять дифференциальные уравнения для решения прикладных задач
2. Ход работы
2.1 Вариант
1) Для некоторой компьютерной фирмы функция маржинальной выручки от продажи своей продукции имеет вид MR = . Здесь MR – маржинальная выручка фирмы, а q – объем продукции. Маржинальная выручка представляет собой производную от общей выручки, причем выручка равна нулю при нулевом уровне продаж. Найти функцию общей выручки. Используя полученную функцию определить:
а) общую выручку, если объём продукции q = штук.
б) объём продукции, который принесёт выручку тысяч рублей.
2) Скорость обесценивания оборудования вследствие его износа пропорциональна в каждый момент времени его фактической стоимости. Начальная стоимость равна тыс.руб, стоимость его через год составила тыс. руб. Запишите формулу для вычисления стоимости оборудования. Используя полученную формулу определить:
а) какова будет стоимость оборудования через года;
б) через сколько лет стоимость оборудования составит тыс. рублей.
3) Сумма тыс. руб. положена в сберегательную кассу на % в год. Найти закон изменения суммы при условии, что приращение начисляется непрерывно и скорость приращения вклада прямо пропорциональна первоначальной величине вклада. Используя полученный закон определить:
а) величину вклада через года;
б) через сколько лет величина вклада составит тыс. рублей.
4) Цена на планшеты некоторой фирмы составляет 13 тыс. рублей. Спрос s и предложение q определены соотношениями: q = p’ + p + , s = 2p’+ p + , где p’ – тенденция формирования цены (производная цены по времени). Определите формулу, по которой должна изменятся цена, чтобы спрос соответствовал предложению. Используя полученную формулу определить:
а) цену планшета через месяца;
б) через сколько месяцев цена планшета будет тыс. рублей.
5) В магазине компьютерной техники начали продажу новой модели смартфона, ежедневно продавали по смартфона. Анализ рынка показал, что можно продавать по
смартфонов в день. Через 1 месяц после начала рекламной компании стали продавать по смартфонов в день. Считая скорость роста продажи смартфонов пропорциональной разности между предельным значением объёма продаж (насыщенным спросом) и её текущим значением, записать закон изменения количества ежедневно продаваемых смартфонов от времени, прошедшего с начала рекламной компании. Используя полученный закон определить:
а) объём продаж через месяца после начала рекламной компании
б) через сколько месяцев после начала рекламной компании объём продаж составит
смартфонов.
2.2  Допуск к работе
Допуск к работе
2.2.1 Известно, что S = C∙e kt и при t = 0 S = 14. Найдите С
__________________________________________________________________________________
2.2.2 Известно, что S = 14∙e kt и при t = 1 S = 28. Найдите e k
__________________________________________________________________________________
2.2.3 Известно, что сумма в 300 тыс. рублей положена под 7% годовых. Найдите сумму вклада через год
__________________________________________________________________________________
2.2.4 Известно, что -ln(6-p) = t + C выразите р
__________________________________________________________________________________
__________________________________________________________________________________
2.2.5 Известно, что Р = 7 + 14∙e kt и при t = 1 Р = 49. Найдите e k
__________________________________________________________________________________
2.2.6 Известно, что р = 40 - C∙e -kt и при t = 0 р = 50. Найдите С
__________________________________________________________________________________
2.2.7 Известно, что р = 40 - 3∙e -kt и при t = 1 р = 70. Найдите e k
__________________________________________________________________________________
2.2.8 Из условия : «Скорость обесценивания оборудования вследствие его износа пропорциональна в каждый момент времени его фактической стоимости.» , получим:
__________S’ = S _______________________________
2.2.9 Из условия : «Скорость приращения вклада прямо пропорциональна первоначальной величине вклада» , получим :
__________ ’ = k _________________________
2.2.10 Из условия: «Считая скорость роста продажи смартфонов пропорциональной разности между предельным значением объёма продаж (насыщенным спросом равным 200 ) и её текущим значением» , получим
__________ p’ = ( -p) ∙ k ________________
К работе допускается ______________
3. Результаты работы
ПРАКТИЧЕСКАЯ РАБОТА 15