Решение дифференциальных уравнений первого порядка
1. Цель работы
1.1. Научиться решать дифференциальные уравнения с разделяющимися переменными.
1.2. Научиться решать однородные дифференциальные уравнения.
1.3. Научиться решать линейные дифференциальные уравнения.
2. Ход работы
2.1 Вариант
Решите уравнения:
1)
2)
3)
4) , у( ) =
5) , у( ) =
6)
7)
8)
9) , у( ) =
10)
2.3 Допуск к работе
2.3.1 Выберите среди данных уравнений дифференциальные:
А) y’=2x2 +sinx; Б) d2 +4d+3=0;
В) y2 +8y’+7=0; Г) y’’-8y’+x=7.
Ответ: __________
2.3.2 Выберите из данных уравнений дифференциальное уравнение первого порядка:
А) y’’=2x2 +sinx; Б) d2 +4d+3=0;
В) y2 +8y’+7=0; Г) y’’-8y’+x=7.
Ответ: __________
2.3.3 Заполните пропуски
Алгоритм решения дифференциального уравнения с разделяющимися переменными
1) Выразить производную функции через дифференциалы 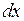 и
и 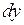
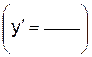
2) Члены с одинаковыми дифференциалами перенести в одну сторону равенства и вынести дифференциал за скобку. ( ) d __ = ( ) d ___
3) Разделить переменные. ( f( ____) ) d __ = ( f( ____) ) d ___
4) Проинтегрировать обе части равенства и найти общее решение.
5) Если заданы начальные условия, то найти частное решение.
2.3.4 Выберите дифференциальное уравнение, полученное в результате разделения переменных 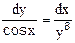 :
:
А) 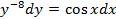 ; Б)
; Б) 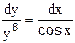 ; В)
; В) 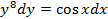 .
.
Ответ: __________
2.3.5 Дано дифференциальное уравнение: 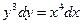 . Тогда его общее решение имеет вид:
. Тогда его общее решение имеет вид:
А) 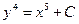 ; Б)
; Б) 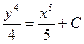 ; В)
; В) 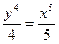 .
.
Ответ: __________
2.3.6  Функция
Функция 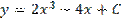 является общим решение некоторого дифференциального уравнения, тогда при
является общим решение некоторого дифференциального уравнения, тогда при 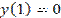 частное решение имеет вид
частное решение имеет вид
А) 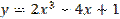 Б)
Б) 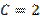
В) 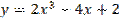 Г)
Г) 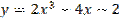
Ответ: __________
2.3.7 Дифференциальное уравнение первого порядка вида:
___________________________
называется однородным, если 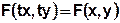
2.3.8 Однородное дифференциальное уравнение приводится к дифференциальному уравнению с разделяющимися переменными
подстановкой ___ y = _______________________
тогда ___ y ‘ = _________________________ , _____ 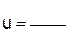 ____
____
2.3.9 Дифференциальное уравнение первого порядка вида:
_________________________________ ,
где 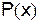 и
и 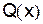 – функции переменной x или постоянные величины, называется линейным дифференциальным уравнением первого порядка, если искомая функция
– функции переменной x или постоянные величины, называется линейным дифференциальным уравнением первого порядка, если искомая функция 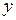 и ее производная
и ее производная 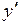 входят в это уравнение в первой степени.
входят в это уравнение в первой степени.
2.3.10 Заполните пропуски
Алгоритм решения линейного дифференциального уравнения первого порядка
1 Привести уравнение к виду 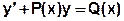 .
.
2 Используя подстановку  , найти
, найти  и подставить эти выражения в уравнения.
и подставить эти выражения в уравнения.
3 Сгру  ппировать члены уравнения и вынести из второго и третьего слагаемых функцию
ппировать члены уравнения и вынести из второго и третьего слагаемых функцию  за скобки.
за скобки.
4 Найти функцию 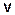 , приравняв выражение в скобках к ________ и решив полученное уравнение. При нахождении функции
, приравняв выражение в скобках к ________ и решив полученное уравнение. При нахождении функции 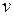 постоянная
постоянная 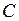 считается равной нулю.
считается равной нулю.
5 Подставить найденную функцию в оставшееся выражение и найти вторую функцию.
6 Записать общее решение, подставив выражения для найденных функций 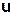 и
и 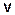 в равенство
в равенство  .
.
7 Если требуется найти частное решение, то определить С из начальных условий и подставить в общее решение.
К работе допускается ______________
3. Результаты работы
 ПРАКТИЧЕСКАЯ РАБОТА 13
ПРАКТИЧЕСКАЯ РАБОТА 13








