Решение прикладных задач с помощью определённого интеграла в Mathcad
1. Цель работы
1.1. Научиться применять определённый интеграл для решения геометрических
задач.
1.2. Научиться применять определённый интеграл для решения физических
задач.
2. Оборудование
 |
Пакет программ MathCAD.
3. Ход работы
3.1 Вариант
3.1.1. Скорость движения тела задаётся формулой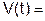 
. Найти путь пройденный телом за сек.
3.1.2. Вычислить силу давления на прямоугольную пластину с основанием
см и высотой см, погружённую вертикально в жидкость плотностью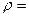 
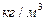так, что верхнее основание находиться на см ниже поверхности жидкости.
3.1.3. Силой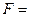 
Н пружина растягивается на см. Первоначальная длина пружины равна см. Какую работу надо совершить, чтобы растянуть пружину до см?
3.1.4. Найти объём тела, полученного при вращении кривой вокруг оси Ох, если
3.1.5. Найти площадь поверхности, полученной при вращении кривой вокруг оси Ох, если
3.1.6. Найти длину кривой между точками
3.1.7. Пластина в виде треугольника с основанием см и высотой см погружена в жидкость, плотности 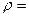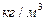. Найти силу давления на пластину, если её вершина лежит на поверхности, а основание параллельно поверхности жидкости.
3.1.8. Найти площадь фигуры, ограниченной линиями:
, если
3.2 Допуск к работе
3.2.1. В чём заключается геометрический смысл определённого интеграла?
_______________________________________________________________________________________________________________________________________________
3.2.2. Как вычислить площадь плоской фигуры, ограниченной графиками двух функций?
_______________________________________________________________________
3.2.3. Как вычислить длину дуги плоской кривой?
_______________________________________________________________________
3.2.4. Какую поверхность называют поверхностью вращения?
_______________________________________________________________________________________________________________________________________________
3.2.5. Как находится объём фигуры, полученной при вращении вокруг оси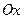 
кривой 
?
_______________________________________________________________________
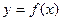3.2.6. Как находится площадь поверхности фигуры, полученной при вращении вокруг оси 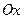кривой ?
_______________________________________________________________________
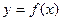3.2.7 В чём заключается физический смысл определённого интеграла?
_______________________________________________________________________________________________________________________________________________
3.2.8 Как вычислить путь, пройденный телом при равномерном движении?
_______________________________________________________________________________________________________________________________________________
3.2.9 Как вычислить путь, пройденный телом при неравномерном движении?
________________________________________________________________________________________________________________________________________________
3.2.10 Как вычислить работу переменной силы?
________________________________________________________________________________________________________________________________________________
3.2.11 Как вычислить силу давления жидкости на вертикально расположенную пластину?
________________________________________________________________________________________________________________________________________________