Кривые второго порядка. Расчёт параметров кривых второго порядка с помощью MathCAD
1. Цель работы
1.1 Научиться составлять уравнения кривых второго порядка
1.2 Научиться находить с помощью пакета MathCAD параметры кривых второго порядка
1.3 Научиться строить с помощью пакета MathCAD кривые второго порядка
2. Оборудование
Пакет программ MathCAD.
3. Ход работы
3.1. Вариант
1. Составить уравнение окружности, ______________________________________
________________________________________________________________
_______________________________________________________________ . Сделать чертёж.
2. Составить уравнение эллипса ________________________________________
________________________________________________________________
_______________________________________________________________ Сделать чертёж.
3. Составить уравнение эллипса ________________________________________
________________________________________________________________
_______________________________________________________________. Сделать чертёж.
4. Составить уравнение гиперболы ______________________________________
________________________________________________________________
_______________________________________________________________. Сделать чертёж.
5. Составить уравнение гиперболы______________________________________
________________________________________________________________
_______________________________________________________________.
Сделать чертёж.
6. Составить уравнение параболы ______________________________________
________________________________________________________________
_______________________________________________________________. Сделать чертёж.
7. Составить уравнение параболы ______________________________________
________________________________________________________________
_______________________________________________________________. Сделать чертёж.
 8. Эллипс задан уравнением
8. Эллипс задан уравнением
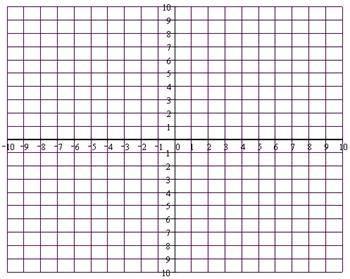
Найти a, b, c, ε, координаты точек F1, F2, A1, A2, B1,B2. Выполнить чертёж.
9. Гипербола задана уравнением
Найти a, b, c, ε, координаты точек F1, F2, координаты вершин, уравнение асимптот. Выполнить чертёж.
10. Найти вершину, фокус, параметр и уравнение директрисы параболы Выполнить чертёж.
3.2 Допуск к работе
3.2.1 Запишите уравнение эллипса, если его полуоси а = 12, b = 5
__________________________________________________________________________
3.2.2 Запишите уравнение гиперболы , если его полуоси а = 12, b = 5
__________________________________________________________________________
3.2.3 Запишите на какой оси находятся фокусы эллипса, заданного уравнением:
А) 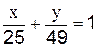 __на оси ______________
__на оси ______________
Б) 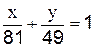 __на оси ______________
__на оси ______________
В) 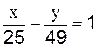 __на оси ______________
__на оси ______________
Г) 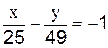 __на оси ______________
__на оси ______________
3.2.4 По данному уравнению параболы укажите координаты вершины и параметр
А) (х - 12) 2 = 12(у + 3) _____ вершина О( ___________) , параметр р= _______
Б) (у - 12) 2 = -16(х + 3) _____ вершина О( ___________) , параметр р= _______
3.2.5 Запишите формулы для вычисления с
| фокусы на оси ОХ | фокусы на оси ОХ | |
| эллипс | ||
| гипербола |
3.2.6 Запишите формулы для вычисления 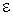
| фокусы на оси ОХ | фокусы на оси ОХ | |
| эллипс | ||
| гипербола |
3.2.7 Запишите уравнение окружности с центром в точке O (-3;2) и радиусом r = 9
__________________________________________________________________________
3.2.8 Укажите координаты центра и радиус окружности, заданной уравнением:
(х - 8)2 + (у + 5)2 = 64 центр О( ___________) , радиус r = _______
К работе допускается ______________
4. Результаты работы
4.8
| a | b | c | ε | F1 | F2 | A1 | A2 | B1 | B2 |

4.9
| a | b | c | ε | F1 | F2 | 1 | 2 | асимптоты |


4.10
| вершина | фокус | параметр | директриса |

 ПРАКТИЧЕСКАЯ РАБОТА 6
ПРАКТИЧЕСКАЯ РАБОТА 6
Применение производной
1. Цель работы
1.1. Научиться применять производную для решения физических и геометрических задач .
2. Ход работы
2.1. Вариант
1) Тело массой кг движется по закону 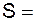 (S в метрах, t в секундах). Найти силу, действующую на тело и его кинетическую энергию через с от начала движения.
(S в метрах, t в секундах). Найти силу, действующую на тело и его кинетическую энергию через с от начала движения.
2) Температура тела изменяется по закону T = (t в секундах, Т в градусах). С какой скоростью изменяется температура тела через с после начала процесса? Что происходит с телом, нагревается оно или охлаждается?
3) Пусть количество вещества, вступившего в химическую реакцию задается зависимостью: 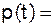 (моль).Найти скорость химической реакции через секунды.
(моль).Найти скорость химической реакции через секунды.
4) Зависимость между количеством х вещества, получаемого в некоторой химической реакции, и временем t выражается уравнением x = A(1 + e - kt) , где А – начальное количество вещества. Определите скорость химической реакции в зависимости от наличия действующего вещества, если
А = , k = , t =
| х | -1,5 | -1,4 | -1,3 | -1,2 | -1,1 | -1 | -0,9 | -0,8 |
| ех | 0,223 | 0,247 | 0,273 | 0,301 | 0,333 | 0,368 | 0,407 | 0,449 |
| х | -0,7 | -0,6 | -0,5 | -0,4 | -0,3 | -0,2 | -0,1 |
| ех | 0,497 | 0,549 | 0,607 | 0,67 | 0,741 | 0,819 | 0,905 |
5) Составьте уравнение касательной и нормали к кривой  в ее точке с абсциссой х0 = .
в ее точке с абсциссой х0 = .
6) Найти приближенное значение функции 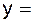 при х = .
при х = .
7) Исследуйте на монотонность и экстремумы функцию 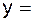 . Постройте схематично график функции.
. Постройте схематично график функции.
8) Исследуйте на выпуклость, вогнутость и точки перегиба функцию 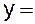
9) Материальная точка движется прямолинейно по закону 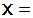 ,
,
t – время в сек, 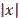 – расстояние от точки до начала координат (м). Найдите наибольшее и наименьшее отклонения точки от начала координат за время t от t0 = c до t1 = c.
– расстояние от точки до начала координат (м). Найдите наибольшее и наименьшее отклонения точки от начала координат за время t от t0 = c до t1 = c.
2.2. Допуск к работе
2.2.1 Заполните таблицу производных:
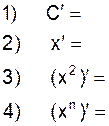
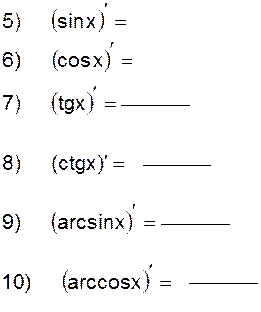
| 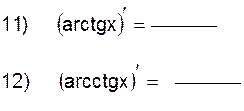
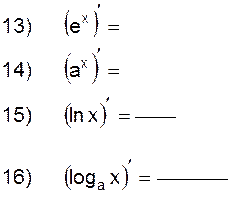
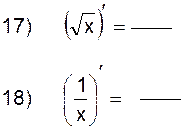
|
2.2.2 Заполните пропуски
А) Если производная дифференцируемой функции положительна на промежутке, то функция на этом промежутке _____________________.
Б) Если производная дифференцированной функции _________________ на промежутке, то функция на этом промежутке убывает.
 |
2.2.3 Дорисуйте схемы
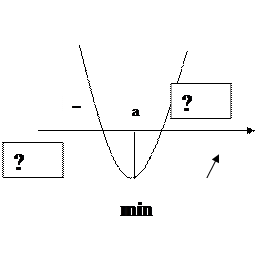 А) Б)
А) Б)
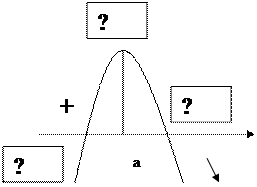
2.2.4 Заполните пропуски:
Пусть материальная точка движется прямолинейно по закону S = S ( t ), тогда
1) Скорость прямолинейного движения материальной точки в момент времени t равно ____________ производной от пути по времени.
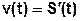
2)  _______________ прямолинейного движения материальной точки в момент времени t равно первой производной от скорости по времени или _____________ производной от пути по времени
_______________ прямолинейного движения материальной точки в момент времени t равно первой производной от скорости по времени или _____________ производной от пути по времени
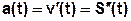
2.2.5 Заполните пропуски:








