2. Дифференциальное уравнение, задача для диф. уравнения.
Формулировки, определения и основные понятия
1. Дифференциальное уравнение, решение, определение, порядок.
2. Дифференциальное уравнение, задача для диф. уравнения.
3. Системы дифференциальных уравнений, определение, порядок
4. Линейно зависимые и линейно независимые функции.
5. Линейные дифференциальные уравнения высшего порядка с нулевой правой частью, фундаментальная система решений.
6. Линейные дифференциальные уравнения высшего порядка с ненулевой правой частью, вид общего решения.
7. Определитель Вронского.
8. Системы дифференциальных уравнений, метод исключений.
9. Однородные линейные системы дифференциальных уравнений с постоянными коэффициентами, вид общего решения, фундаментальная система решений.
Вопросы
1. Теорема существования решения задачи Коши для дифференциального уравнения первого порядка.
2. Дифференциальное уравнение первого порядка с разделяющимися переменными.
3. Однородное дифференциальное уравнение первого порядка.
4. Дифференциальные уравнения, сводящиеся к однородным.
5. Линейное дифференциальное уравнение первого порядка. Метод вариации произвольной постоянной.
6. Уравнение Бернулли. Метод вариации произвольной постоянной.
7. Дифференциальное уравнение первого порядка в полных дифференциалах.
8. Интегрирование дифференциальных уравнений высших порядков путем понижения порядка уравнения, различные способы понижения порядка дифференциального уравнения.
9. Линейно зависимые и линейно независимые решения линейного дифференциального уравнения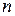 
-го порядка. Определитель Вронского.
10. Вид общего решения линейного дифференциального уравнения высшего порядка с ненулевой правой частью.
11. Метод вариации произвольных постоянных решения линейного дифференциального уравнения высшего порядка с ненулевой правой частью.
12. Линейные дифференциальные уравнения высшего порядка с постоянными коэффициентами с нулевой правой частью, случай действительных различных корней характеристического уравнения.
13. Линейные дифференциальные уравнения высшего порядка с постоянными коэффициентами с нулевой правой частью, случай комплексных корней характеристического уравнения.
14. Линейные дифференциальные уравнения высшего порядка с постоянными коэффициентами с ненулевой правой частью, правая часть специального вида.
15. Однородные линейные системы дифференциальных уравнений с постоянными коэффициентами. Матричный метод, случай различных действительных корней характеристического уравнения.
16. Однородные линейные системы дифференциальных уравнений с постоянными коэффициентами. Матричный метод, случай кратных действительных корней характеристического уравнения, корневые векторы.
17. Однородные линейные системы дифференциальных уравнений с постоянными коэффициентами. Матричный метод, случай комплексных корней характеристического уравнения.
18. Линейные системы дифференциальных уравнений с постоянными коэффициентами с ненулевой правой частью. Метод вариации.
Ряды Фурье
1. Пространство функций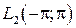 
, скалярное произведение, норма, ортогональный базис.
2. Неравенство Бесселя. Равенство Парсеваля - Стеклова.
3. Разложение периодической функции в тригонометрический ряд Фурье на интервале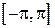 
.
4. Разложение функции в тригонометрический ряд Фурье на произвольном интервале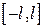 
.
5. Разложение функции в тригонометрический ряд Фурье на полуинтервале
6. Ряд Фурье в комплексной форме.
7. Интеграл и преобразование Фурье.