Тема: «Дифференцирование функции, исследование функций и построение графиков»
Практическое занятие № 2
Тема: «Дифференцирование функции, исследование функций и построение графиков»
Цель: 1.Сформировать навык нахождения производных функций и экстремумов, интервалов монотонности и выпуклости – вогнутости и точек перегиба функции с использованием производной первого и второго порядков в ходе решения упражнений.
2. Способствовать развитию умения использовать полученные знания для достижения поставленных задач.
3. Способствовать привитию сознательного приобретения новых знаний по теме.
Теоретические сведения к практической работе:
Производной функции у= f( x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):
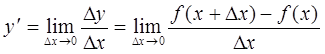
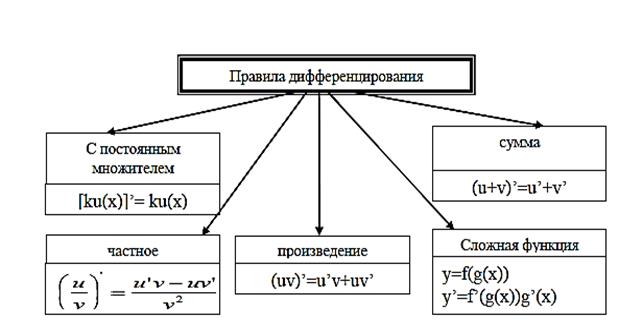
Правило дифференцирования сложной функции. Если функция y = f(u) дифференцируема по и, а функция и = φ (x) — по х, то сложная функция y = f(φ (x)) имеет производную y ' = f ' ( u ) ∙ u ' ( x ) .
Таблица производных элементарных функций
1. 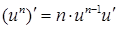 . .
| 5. 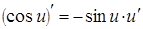 . .
|
1а. 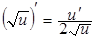 . .
| 6. 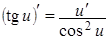 . .
|
1б. 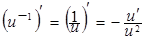 . .
| 7. (ctgu) 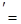 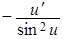 . .
|
2. 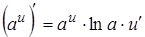 . .
| 8. 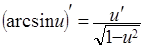 . .
|
2а. 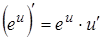 . .
| 9. 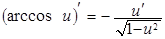 . .
|
3. 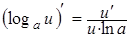 . .
| 10. 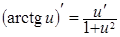 . .
|
3а. 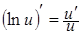 . .
| 11. |
4. 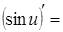 cosu × u¢. cosu × u¢.
|
Переменная y = f(x) является функцией от переменной x, если задана такая зависимость между этими переменными, которая позволяет для каждого значения x однозначно определить значение переменной y.
Совокупность всех тех значений, которые принимает аргумент х функции y =f(x), называется областью определения этой функции. Обозначается D(f).
Совокупность всех тех значений, которые принимает сама функция у, называется областью изменения этой функции. Обозначается E(f).
Нули функции – точки, в которых функция обращается в нуль. Это решения уравнения f(x)=0 (точки пересечения графика с осью Ох).
Промежутки знакопостоянства функции – интервалы, на которых функция положительна (график расположен выше оси Ох) или отрицательна (график расположен ниже оси Ох). Это решения неравенств f(x)> 0 и f(x)< 0.
Функция y = f(x) называется чётной, если при всех значениях аргумента f(–x)= f(x).
Функция y = f(x) называется нечётной, если при всех значениях аргумента f(–x)= –f(x). При этом имеется в виду, что если х входит в область определения, то и – х также входит в область определения.
Функция y = f(x) называется периодической, если существует такое число Т>0, что выполняется равенство f (x)= f (х±Т), верное при всех х.
Критическими точками функции y = f(x) называются точки, в которых производная обращается в нуль, а также точки, в которых производная не существует.
Точки экстремума функции – точки, лежащие внутри области определения, в которых функция принимает или самое большое (max) значение, или самое малое (min) значение по сравнению со значениями в близких точках. Экстремумом функции называется значение функции в точке экстремума.
Промежутки монотонности - это промежутки возрастания и убывания функции, т. е. интервалы, на которых функция или возрастает или убывает.
Кривая называется выпуклой вверх (выпуклой) на промежутке [a;c), если все точки кривой лежат ниже любой её касательной на [a;c), где а< с < в (f ”(x)<0).
Кривая называется выпуклой вниз (вогнутой) на промежутке [c;b), если все точки кривой лежат выше любой её касательной на [c;b), (f”(x)> 0).
Точка М кривой, которая отделяет выпуклость от вогнутости, называется точкой перегиба графика функции.
Методические указания к выполнению заданий:
Указание для задания № 1: Найдите производную функции, используя основные формулы дифференцирования.
Указание для задания № 2: Найдите производную сложной функции, используя алгоритм.

Указание для задания № 3: Правило исследования дифференцируемой функции у=f(x) на экстремум:
1) Найти область определения функции.
2) Найти производную 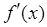 .
.
3) Найти точки, в которых выполняется равенство 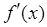 =0.
=0.
4) Найти точки, в которых 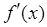 не существует.
не существует.
5) Отметить на координатной прямой все критические точки и область определения функции у=f(x); получатся промежутки области определения функции, на каждом из которых производная функции у=f(x) сохраняет знак.
6) Определить знак 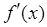 на каждом из промежутков, полученных в п.5.
на каждом из промежутков, полученных в п.5.
7) Сделать выводы о наличии или отсутствии экстремума в каждой из критических точек в соответствии с достаточным условием экстремума:
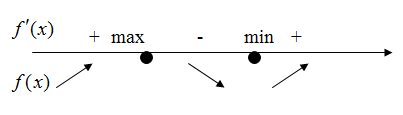
Указание для задания №4: Правило нахождения экстремумов функции у=f(x) с помощью второй производной:
1) Найти производную 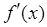 .
.
2) Найти критические точки данной функции, в которых 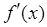 =0.
=0.
3) Найти вторую производную 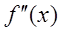 .
.
4) Исследовать знак второй производной в каждой из критических точек. Если при этом вторая производная окажется отрицательной, то функция в такой точке имеет максимум, а если положительной, то – минимум. Если же вторая производная равна нулю, то экстремум функции надо искать с помощью первой производной.
5) Вычислить значения функции в точках экстремума.
Указание для задания №5: Правило исследования дифференцируемой функции у=f(x) на выпуклость и точки перегиба:
1) Найти область определения функции: Df.
2) Найти вторую производную функции f ″ (x).
3) Найти критические точки функции y = f(x) , в которых f ″ (x) обращается в нуль или терпит разрыв.
4) Исследовать знак второй производной f ″ (x) в промежутках, на которые найденные критические точки делят область определения функции y = f(x), используя достаточные условия выпуклости функции. Если при этом критическая точка хо разделяет промежутки выпуклости противоположных направлений, то хо является абсциссой точки перегиба функции.
5) Вычислить значения функции в точках перегиба.
 ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ СТУДЕНТАМИ:
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ СТУДЕНТАМИ:
| Вариант - 1 | Вариант - 2 |
| 1. Найдите производную следующих функций: | |
а) 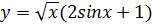 б)
б) 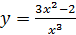 в)
в) 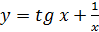
| а) 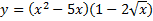 б)
б) 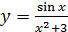 в)
в) 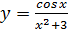
|
| 2. Найдите производную сложных функций: | |
а) 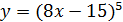 б)
б) 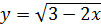 в)
в) 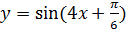 г)
г) 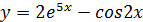 д)
д) 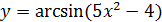 е)
е) 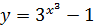
| а) 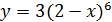 б)
б) 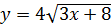 в)
в) 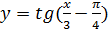 г)
г) 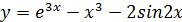 д)
д) 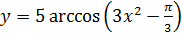 е)
е) 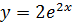
|
| 3. Найдите экстремумы и интервалы монотонности ( с помощью первой производной) функции: | |
а) 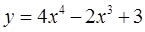  б)
б) 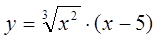
| а) 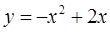  б)
б) 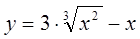
|
| 4. Найдите экстремумы и интервалы монотонности (с помощью второй производной) функции и постройте график функции: | |
а) 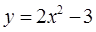 б)
б) 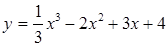
| а) 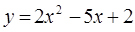 б)
б) 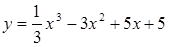
|
| 5. Исследовать функции на направление выпуклости и точки перегиба: | |
а) 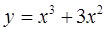 б)
б) 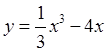 в)
в) 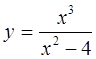
| а) 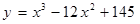 б)
б) 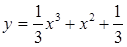 в)
в) 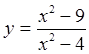
|
| Вариант - 3 | Вариант -4 |
| 1. Найдите производную следующих функций: | |
а) 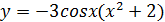 б)
б) 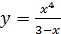 в)
в) 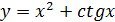
| а) 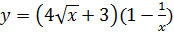 б)
б) 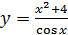 в)
в) 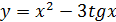
|
| 2. Найдите производную сложных функций: | |
а) 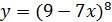 б)
б) 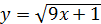 в)
в) 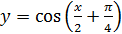 г)
г) 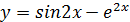 д)
д) 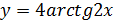 е)
е) 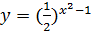
| а) 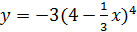 б)
б) 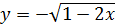 в)
в) 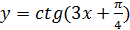 г)
г) 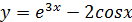 д)
д) 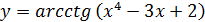 е)
е) 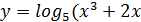 -4) -4)
|
| 3. Найдите экстремумы и интервалы монотонности ( с помощью первой производной) функции: | |
а) y = x2 – 5x + 4
б) 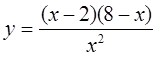
| а) y =2 x3 + 3x2 – 5
б) 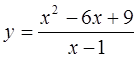
|
| 4. Найдите экстремумы и интервалы монотонности (с помощью второй производной) функции постройте график функции: | |
а) y = x3 + 6x2 +9x + 4
б) 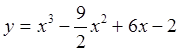
| а) y = – x3+ x2
б) 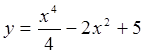
|
| 5. Исследовать функции на направление выпуклости и точки перегиба: | |
а) у = х3 - 3х2 + 4
б) y = x3– x2
в) 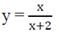
|
а) у = х3 - х2 -х+ 5
б) y = – x3+ x2
в) 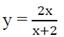
|
| Вариант - 5 | Вариант -6 |
| 1. Найдите производную следующих функций: | |
а) 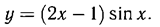 б)
б) 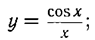 в)
в) 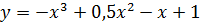
| а) 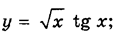 б)
б) 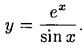 в)
в) 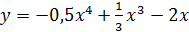
|
| 2. Найдите производную сложных функций: | |
а) y = (3x2- 5x + 2)21;
б) y = 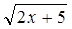 ;
в) y =sin (2x + 3)
г) y= e-2x+7
д) ;
в) y =sin (2x + 3)
г) y= e-2x+7
д) 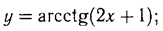 е)
е) 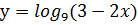
| а) y = (3x2- 5x + 2)21;
б) y = 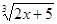 ;
в) y =cos (2x + 3)
г) y= ;
в) y =cos (2x + 3)
г) y= 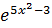 д) y = arctg(2x+1)
е)
д) y = arctg(2x+1)
е) 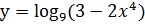
|
| 3. Найдите экстремумы и интервалы монотонности ( с помощью первой производной) функции: | |
а) 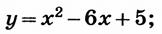 б)
б) 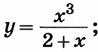
| а) 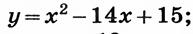 б)
б) 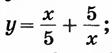
|
| 4. Найдите экстремумы и интервалы монотонности (с помощью второй производной) функции постройте график функции: | |
а) 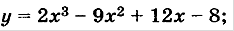 б)
б) 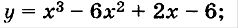
| а) 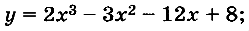 б)
б) 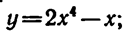
|
| 5. Исследовать функции на направление выпуклости и точки перегиба: | |
а) 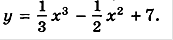 б)
б) 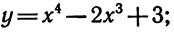 в)
в) 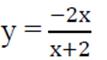
| а) 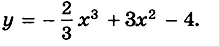 б)
б) 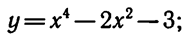 в)
в) 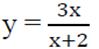
|
Выполненную и правильно оформленную работу предоставить преподавателю.









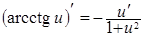 .
.