Практическая работа
«Решение тригонометрических уравнений»
ЦЕЛЬ РАБОТЫ:
1. Закрепить навыки определения типов тригонометрических уравнений (простейшее, квадратное относительно 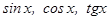 , однородное относительно
, однородное относительно 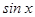 и
и 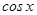 , уравнение, решаемое разложением на множители левой части).
, уравнение, решаемое разложением на множители левой части).
2. Усвоить алгоритмы решения основных типов тригонометрических уравнений.
ОБОРУДОВАНИЕ: карты индивидуальных заданий, таблицы значений тригонометрических функций некоторых углов, таблицы частных случаев решения простейших тригонометрических уравнений, таблицы формул тригонометрии, микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Ответить на контрольные вопросы:
а) Дайте определения арксинуса, арккосинуса арктангенса и арккотангенса числа а.
б) Перечислите свойства обратных тригонометрических функций.
в) Вспомните формулы, с помощью которых решают простейшие тригонометрические уравнения.
г) Какой вид имеет квадратное относительно 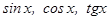 тригонометрическое уравнение? Объясните алгоритм его решения.
тригонометрическое уравнение? Объясните алгоритм его решения.
д) Какой вид имеет однородное относительно 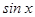 и
и 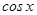 тригонометрическое уравнение? Какова методика его решения?
тригонометрическое уравнение? Какова методика его решения?
е) Вспомните формулы, с помощью которых решают простейшие тригонометрические уравнения.
2. По образцу выполнить тренировочные задания.
3. Изучить условие задания для самостоятельной работы.
4. Оформить отчет о работе.
УКАЗАНИЯ К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ:
ПРИМЕР 1. Вычислите: 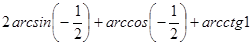 .
.
РЕШЕНИЕ.
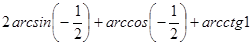 =
= 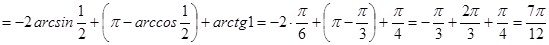 .
.
ЗАДАНИЯ ДЛЯ САМОКОНТРОЛЯ.
Вычислите: а) 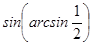 ; б)
; б) 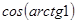 ; в)
; в) 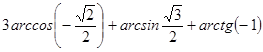 ; г)
; г) 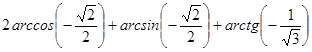 .
.
ПРИМЕР 2. Решите уравнение: 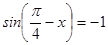 .
.
РЕШЕНИЕ.
По формуле частного случая: 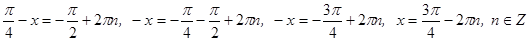 .
.
ПРИМЕР 3. Решите уравнение: 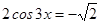 .
.
РЕШЕНИЕ.
Разделим левую и правую части уравнения на 2: 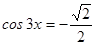 .
.
По формуле 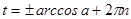 получаем:
получаем: 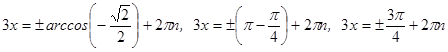 .
.
Разделим левую и правую части уравнения на 3: 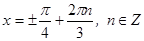 .
.
ПРИМЕР 4. Решите уравнение: 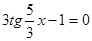 .
.
РЕШЕНИЕ.
Выразим 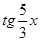 :
: 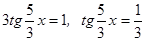 .
.
По формуле 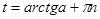 получаем:
получаем: 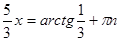 .
.
Разделим левую и правую части уравнения на 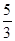 :
: 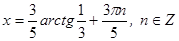 .
.
ЗАДАНИЯ ДЛЯ САМОКОНТРОЛЯ.
Решите уравнения: а) 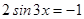 ; б)
; б) 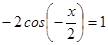 ; в)
; в) 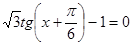 .
.
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ
Вариант 1
1. Вычислите: 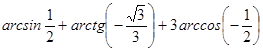 .
.
2. Решите уравнения: а) 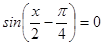 ; б)
; б) 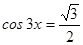 ; в)
; в) 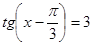 .
.
Вариант 2
1. Вычислите: 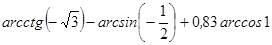 .
.
2. Решите уравнения: а) 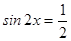 ; б)
; б) 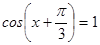 ; в)
; в) 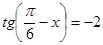 .
.
Вариант 3
1. Вычислите: 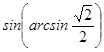 .
.
2. Решите уравнения: а) 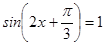 ; б)
; б) 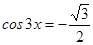 ; в)
; в) 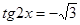 .
.
Вариант 4
1. Вычислите: 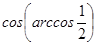 .
.
2. Решите уравнения: а) 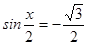 ; б)
; б) 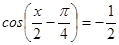 ; в)
; в) 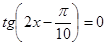 .
.
Вариант 5
1. Вычислите: 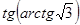 .
.
2. Решите уравнения: а) 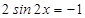 ; б)
; б) 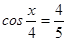 ; в)
; в) 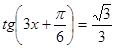 .
.
Вариант 6
1. Вычислите: 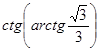 .
.
2. Решите уравнения: а) 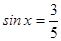 ; б)
; б) 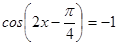 ; в)
; в) 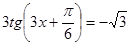 .
.
Вариант 7
1. Вычислите: 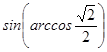 .
.
2. Решите уравнения: а) 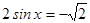 ; б)
; б) 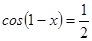 ; в)
; в) 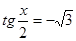 .
.
Вариант 8
1. Вычислите: 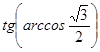 .
.
2. Решите уравнения: а) 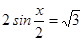 ; б)
; б) 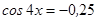 ; в)
; в) 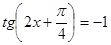 .
.
Вариант 9
1. Вычислите: 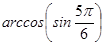 .
.
2. Решите уравнения: а) 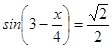 ; б)
; б) 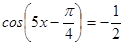 ; в)
; в) 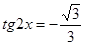 .
.
Вариант 10
1. Вычислите: 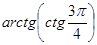 .
.
2. Решите уравнения: а) 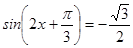 ; б)
; б) 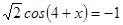 ; в)
; в) 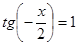 .
.
УКАЗАНИЯ К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ:
ПРИМЕР 1. Решите уравнение: 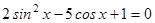 .
.
РЕШЕНИЕ. Применив основное тригонометрическое тождество: 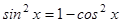 , получим:
, получим:
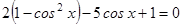 ,
,
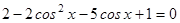 ,
,
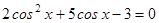 .
.
Это уравнение является квадратным относительно 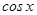 . Обозначим
. Обозначим 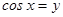 , тогда
, тогда 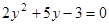 . Полученное уравнение имеет решения
. Полученное уравнение имеет решения
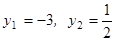 .
.
Составим два простейших уравнения:
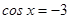 и
и 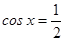 .
.
Первое уравнение решений не имеет, так как 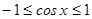 . Второе уравнение имеет решение:
. Второе уравнение имеет решение:
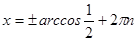 ,
,
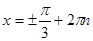 .
.
Ответ: 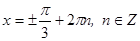
ПРИМЕР 2. Решите уравнение: 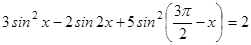 .
.
РЕШЕНИЕ.
Так как по формуле приведения 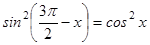 , а
, а 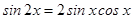 по формуле двойного угла, то
по формуле двойного угла, то
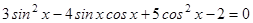 .
.
При помощи основного тригонометрического тождества заменим 2 на 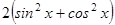 и получим:
и получим:
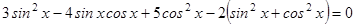 ,
,
откуда
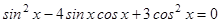 .
.
Это уравнение является однородным относительно 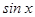 и
и 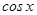 . Разделив обе части полученного уравнения на
. Разделив обе части полученного уравнения на 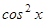 , получим
, получим
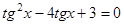 .
.
Это уравнение является квадратным относительно 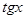 . Обозначим
. Обозначим 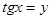 , тогда
, тогда 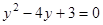 . Полученное квадратное уравнение имеет корни
. Полученное квадратное уравнение имеет корни 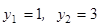 . Из уравнения
. Из уравнения 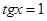 получаем
получаем
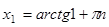 ,
,
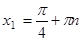 .
.
Из уравнения 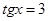 получаем
получаем
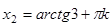 .
.
Ответ: 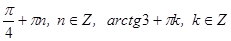
ПРИМЕР 3. Решите уравнение: 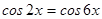 .
.
РЕШЕНИЕ.
Запишем данное уравнение иначе:
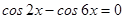 .
.
По формуле разности косинусов 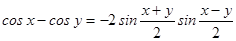 получаем:
получаем:
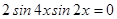 .
.
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Поэтому если 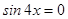 , то
, то 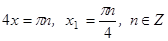 ; если
; если 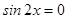 , то
, то 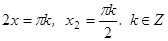 .
.
Можно заметить, что вторая серия решений содержится в первой и иначе записать ответ.
Ответ: 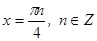 .
.
ПРИМЕР 4. Решите уравнение: 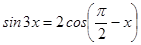 .
.
РЕШЕНИЕ.
В правой части применим формулу приведения
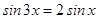 ,
,
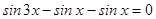 ,
,
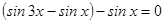 .
.
Применим формулу разности синусов 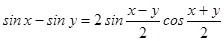 , тогда
, тогда
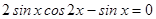 .
.
Вынесем за скобки общий множитель:
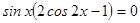 .
.
Если 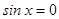 , то
, то 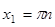 ; если
; если 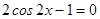 , то
, то 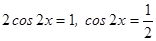 , значит,
, значит, 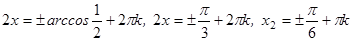 .
.
Ответ: 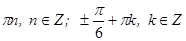 .
.
ЗАДАНИЯ ДЛЯ САМОКОНТРОЛЯ.
Решите уравнения: а) 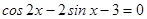 ; б)
; б) 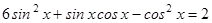 ; в)
; в) 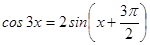 .
.
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ.
Вариант 1
Выясните, к какому типу относятся данные тригонометрические уравнения, и решите их:
1. 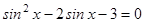 ;
;
2. 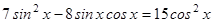 ;
;
3. 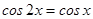 ;
;
4. 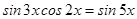 .
.
Вариант 2
Выясните, к какому типу относятся данные тригонометрические уравнения, и решите их:
1. 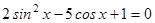 ;
;
2. 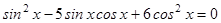 ;
;
3. 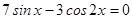 ;
;
4. 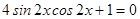 .
.
Вариант 3
Выясните, к какому типу относятся данные тригонометрические уравнения, и решите их:
1. 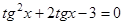 ;
;
2. 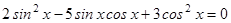 ;
;
3. 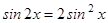 ;
;
4. 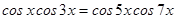 .
.
Вариант 4
Выясните, к какому типу относятся данные тригонометрические уравнения, и решите их:
1. 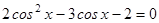 ;
;
2. 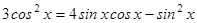 ;
;
3. 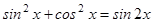 ;
;
4. 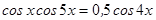 .
.
Вариант 5
Выясните, к какому типу относятся данные тригонометрические уравнения, и решите их:
1. 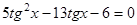 ;
;
2. 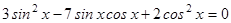 ;
;
3. 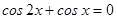 ;
;
4. 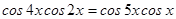 .
.
Вариант 6
Выясните, к какому типу относятся данные тригонометрические уравнения, и решите их:
1. 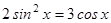 ;
;
2. 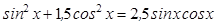 ;
;
3. 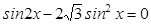 ;
;
4. 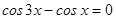 .
.
Вариант 7
Выясните, к какому типу относятся данные тригонометрические уравнения, и решите их:
1. 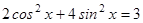 ;
;
2. 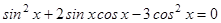 ;
;
3. 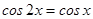 ;
;
4. 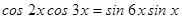 .
.
Вариант 8
Выясните, к какому типу относятся данные тригонометрические уравнения, и решите их:
1. 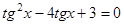 ;
;
2. 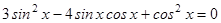 ;
;
3. 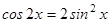 ;
;
4. 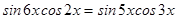 .
.
Вариант 9
Выясните, к какому типу относятся данные тригонометрические уравнения, и решите их:
1. 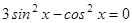 ;
;
2. 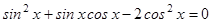 ;
;
3. 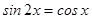 ;
;
4. 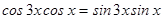 .
.
Вариант 10
Выясните, к какому типу относятся данные тригонометрические уравнения, и решите их:
1. 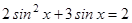 ;
;
2. 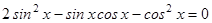 ;
;
3. 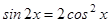 ;
;
4. 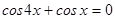 .
.








