Тема: «Применение определенного интеграла для нахождения площади криволинейной трапеции.»
Практическое занятие № 4
Тема: «Применение определенного интеграла для нахождения площади криволинейной трапеции.»
Цель: 1. Сформировать навыки вычисления площади плоской фигуры с помощью определенного интеграла, в ходе решения упражнений.
2. Способствовать развитию логического мышления, памяти, внимания.
3. Способствовать привитию сознательного приобретения новых знаний по теме.
Теоретические сведения к практической работе:
Определенный интеграл широко применяется при вычислениях различных геометрических и физических величин. Вычисление некоторой величины и, соответствующей промежутку а ≤ x ≤ bизменения независимой величины х выполняется по формуле S = 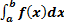 .
.
Площади фигур.
 у у
у у
S 
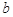 х
х
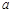
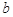 х S
х S
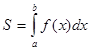
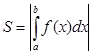
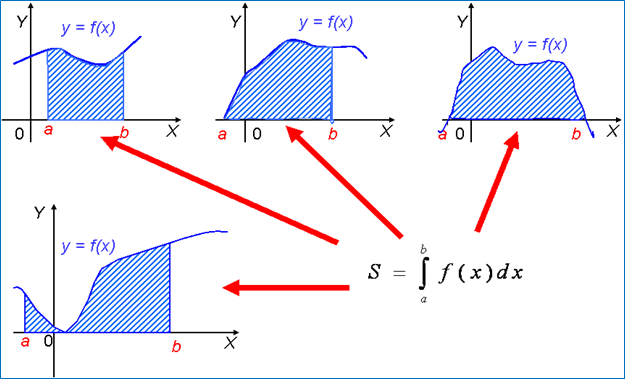
Если рассмотренная фигура не является криволинейной трапецией, тогда площадь нужно представить как сумму или разность криволинейных трапеций.
 |  |
m
n
S1 S2
a b
S = S1 + S2 S = S amb – S anb
Методические указания к выполнению заданий:
Указание для задания № 1: для выполнения воспользуйтесь следующим алгоритмом
Алгоритм:
1) Сделать график заданных функций, ограничивающих площадь плоских фигур.
2) Найти пределы интегрирования.
3) Выяснить какой формулой площади плоской фигуры удобно пользоваться в данном случае.
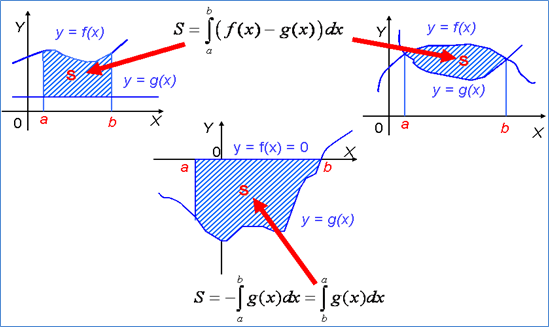
а) Фигура, ограничена графиком непрерывной и неотрицательной на отрезке [ а,b] функции y=f (x), осью Ox и прямыми x=a и x=b:
S= 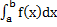 ;
;
б) Фигура, ограничена графиком непрерывной и неположительной на отрезке [ а,b] функции y=f (x), осью Ox и прямыми x=a и x=b:
S= 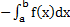 или S=
или S= 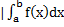 |
|
в) Фигура, ограничена осью Ox, прямыми x=a и x=b, и графиком непрерывной на отрезке [ а,b] ,функции y=f (x), которая меняет свой знак конечное число раз на этом отрезке:
S= 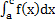 -
- 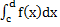 +
+ 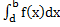 |
|
г)Пусть требуется вычислить площадь фигур, ограниченной кривыми y= 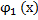 и y=
и y= 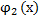 , и прямыми x=a b x=b, где a
, и прямыми x=a b x=b, где a 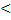 b и
b и 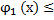
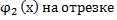 [ а,b], то необходимо воспользоваться формулой:
[ а,b], то необходимо воспользоваться формулой:
S= 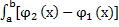 dx
dx
4) Вычислить площадь заданной фигуры.
Пример 1: Вычислить площадь фигуры, ограниченной линиями: х + 2у – 4 = 0, у = 0, х = -3, х =2.
Решение:
1) х+2у-4=0 – прямая линия.
у=0 – ось ОХ, х = -3–прямая параллельная оси ОУ, проходящая через точку (-3;0).
х=2 – прямая параллельная ОУ (2;0), проходящая через точку (2;0)
х+2у-4=0;
х+2у=4 Þ у=- 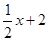
| х | 0 | 4 |
| у | 2 | 0 |
2) Построим график функции:
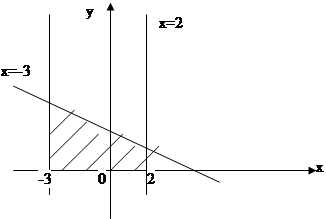
у= - 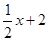
|
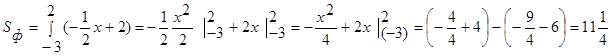 (ед2).
(ед2).
Пример 2: Вычислить площадь фигуры, ограниченной линиями: 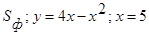 .
.
Решение:
1)Вершина параболы: 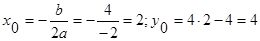
2) Ветви вниз, корни 4х-х2=0 х(4-х)=0
х1=0, х2=4
3) х=5 – прямая, параллельная оси ОУ ,проходящая через точку (5; 0).
Если фигура располагается ниже оси ОХ, то ее площадь вычисляется по абсолютной величине (модулю):
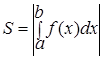
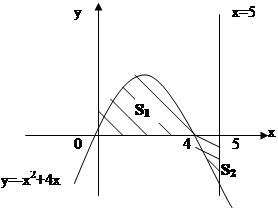 | |||
| |||
Разбиваем фигуру на две части : 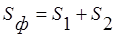
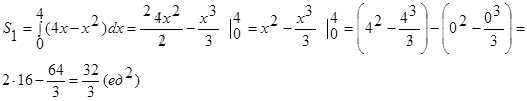
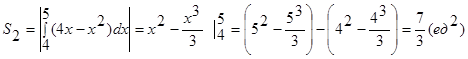
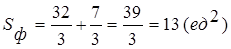
 ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ СТУДЕНТАМИ:
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ СТУДЕНТАМИ:
| Вариант - 1 | Вариант - 2 |
| 1. Найдите площади фигур, ограниченных линиями: | |
а) y= -x2 +9 и y=0
б) y= x2 и y= 2x+3
в) y=  , y=0, x=1 и x=5 , y=0, x=1 и x=5
| а) y= -x2 +16 и y=0
б) y= x2 и y= 4x-3
в) y=  , y=0, x=1 и x=6 , y=0, x=1 и x=6
|
| 2. Вычислить площадь заштрихованной фигуры, изображенной на рисунке: | |
а)
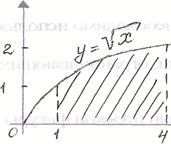 б)
б)
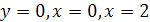 в)
в
в)
в
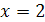 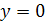 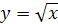 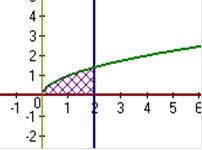
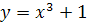 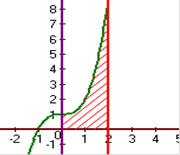
|
а)
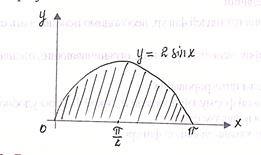 б)
в)
б)
в)
 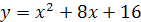 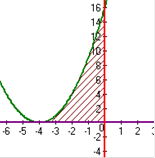 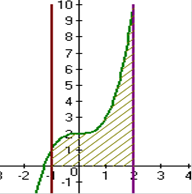 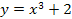 , , 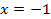 , , 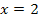
|
| Вариант - 3 | Вариант -4 |
| 1. Найдите площади фигур, ограниченных линиями: | |
а) y=  x3, x= -2,x=4 y=0
б) y= x2-x-5 и y= x-2
в) y= x3, x= -2,x=4 y=0
б) y= x2-x-5 и y= x-2
в) y= 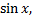 y=0, x= y=0, x= 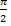 и x= и x= 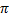
| а) y= 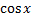 , y= 0, x= , y= 0, x= 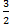 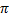 , x=0
б) y= x2+5 и y= x+3
в) y= , x=0
б) y= x2+5 и y= x+3
в) y= 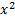 , y= 2x , y= 2x
|
| 2. Вычислить площадь заштрихованной фигуры, изображенной на рисунке: | |
а) 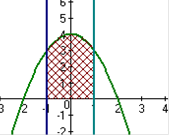 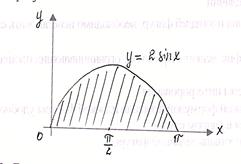 б)
б)
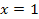 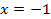 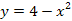 в)
в) 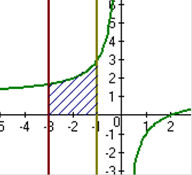
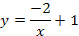
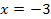 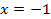
|
а) 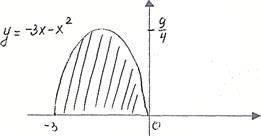 б)
б)
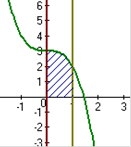 y= x3, x=0, x = 1
в)
y= x3, x=0, x = 1
в) 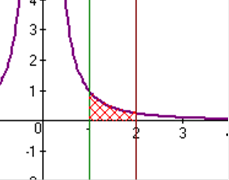
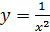 , x=1, x = 2 , x=1, x = 2
|
| Вариант - 5 | Вариант - 6 |
| 1. Найдите площади фигур, ограниченных линиями: | |
а) 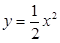 и и 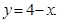 б)
б) 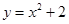 и и 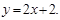 в) у= -х2+2х+3, у=3-х
в) у= -х2+2х+3, у=3-х
| а) 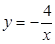 и и 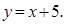 б)
б) 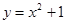 и и 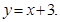 в) у=
в) у= 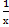 , у= -х2+4х-2 , у= -х2+4х-2
|
| 2. Вычислить площадь заштрихованной фигуры, изображенной на рисунке: | |
а)
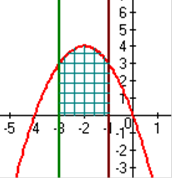 y = -x2 – 4x, x= -3, x= -1
б)
y = -x2 – 4x, x= -3, x= -1
б) 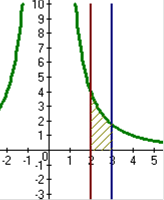
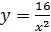 , x=2, x=3
в) , x=2, x=3
в)
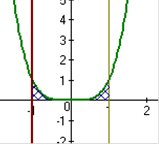 y= x4, x= -1, x=1 y= x4, x= -1, x=1
| а) 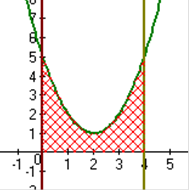
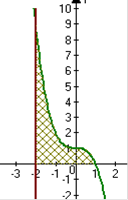 y = x 2 - 4 x + 5, x =0, x = 4
б)
y = 1 – x 3 , x =-2, x =1
в)
y = x 2 - 4 x + 5, x =0, x = 4
б)
y = 1 – x 3 , x =-2, x =1
в)
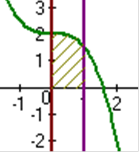 y = - y = -  x 3 + 2, x =0, x =1, y=0 x 3 + 2, x =0, x =1, y=0
|
Выполненную и правильно оформленную работу предоставить преподавателю.








