Урок Практическая работа «Логарифмические неравенства»
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
Урок Практическая работа «Логарифмические неравенства»
Цели:Формирование навыков решения логарифмических неравенств, использования свойств логарифмов при решении неравенств.
Простейшее логарифмическое неравенство имеет вид:
1. 
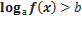
2. 
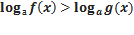
Могут быть любые знаки неравенства: <,>, ≤ или ≥.При этом основание логарифма всегда положительно a>0.
1. Применяем свойство логарифма: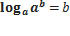 
, получаем неравенство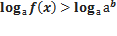 
Возникает ОДЗ: f ( x )>0.
Общий вид логарифмических неравенств: .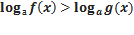
ПРАВИЛО:
Если основание логарифма больше единицы (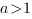 
) , то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства сохраняется, и неравенство
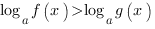
равносильно системе:
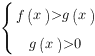
Если основание логарифма больше нуля и меньше единицы (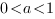 
), то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный, и неравенство
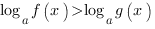
равносильно системе:
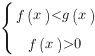
Примеры решения логарифмических неравенств.
1. Решим неравенство:
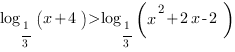
Так как основание логарифмов в обеих частях неравенства меньше 1, при переходе к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный. Выражения, стоящие под знаком логарифма должны быть строго больше нуля. Перейдем к системе:
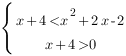
Обратите внимание: мы указываем, что больше нуля должно быть меньшее из выражений, которые стоят под знаком логарифма. В этом случает большее выражение автоматически будет больше нуля.
Решим систему неравенств:
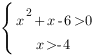
Корни квадратного трехчлена: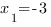 
, 
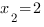
Отсюда совместное решение на числовой оси:
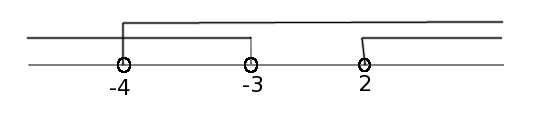
Ответ: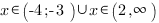 
2. Решим неравенство:
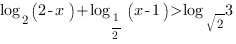
Мы видим, что в основании логарифмов стоят степени числа 2, поэтому мы можем привести логарифмы к одному основанию. Сделаем это, воспользовавшись свойствами логарифмов:
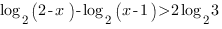
Перенесем логарифм с отрицательным коэффициентом из левой части неравенства в правую (так как умножать легче, чем делить).
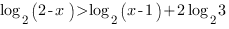
Так как в неравенстве присутствуют логарифмы с одинаковым основанием и в первой степени, мы можем представить обе части неравенства в виде логарифма по основанию 2:
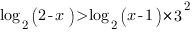
Теперь мы можем перейти от логарифмов к выражениям, стоящим под знаком логарифма.
Основание больше 1, поэтому знак неравенства сохраняется. Не забываем про ОДЗ:
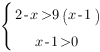
Отсюда:
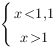
Ответ: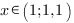 
АЛГОРИТМ РЕШЕНИЯ ЛОГАРИФМИЧЕСКИХ НЕРАВЕНСТВ
1. Запис ать ОДЗ ( выражение под логарифмом должно быть положительно
2. Преобразовать , если необходимо, логарифмическое неравенство так, чтобы логарифмы были и слева, и справа( используя свойства логарифмов)
3. Проанализировать основание логарифма
4. Опустить знаки логарифма, записать полученное неравенство, по правилу:
Если основание логарифмов в обеих частях неравенства меньше 1, при переходе к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный. Если основание логарифма больше единицы ( 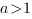) , то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства сохраняется.
5. Решить полученное неравенство совместно с ОДЗ.
Решить неравенство:
1.) 
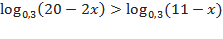
2.) 
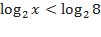
3.) 
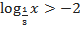
4.) 
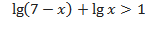
5.) 
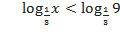
6.) 
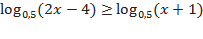
7.) 
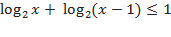
8.) 
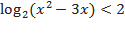
9.) 
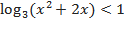
Решить: № 355 , 356, 357.