Лекция-практика К вадратные неравенства
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
Лекция-практика К вадратные неравенства
Цели урока: повторить основные понятия, связанные с неравенствами и их системами; формирование навыков решения линейных неравенств.
Квадратные неравенства – неравенства вида 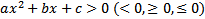
Неравенства решаются методом интервалов или графическим способом.
Смотрим презентацию.
Метод интервалов- алгоритм
| Алгоритм | Примечания |
| 1. Неравенства решаются относительно нуля | Если справа не ноль, перенести все слагаемые в левую часть |
| 2. Найти корни всех сомножителей | Для дробно-рациональных неравенств находим отдельно корни числителя и знаменателя ( найти корни – значить приравнять выражение к нулю и решить полученное уравнение) |
| 3. Нанести корни на числовую ось, учитывая «строгость « неравенства Корни знаменателя всегда выколоты! | «Строгость» определяем по знаку неравенства :>, < - строгое ( на рис. Точка выколота, скобки в ответе круглые), 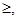 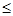 - не строгое, ( на рис. Точка закрашена, скобки в ответе – квадратные, - не строгое, ( на рис. Точка закрашена, скобки в ответе – квадратные, 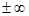 - скобки всегда круглые - скобки всегда круглые
|
| 4. Определить знак выражения справа от большего корня | Знак определяем по произведению старших коэффициентов ( старший коэффициент- коэффициент при старшей степени переменной) |
| 5. Расставить знаки в остальных интервалах , учитывая, четное или нечетное число раз встречается каждый корень | «Нечетный «корень- знак меняется, «четный «корень- знак не меняется. |
Задание 1. Решить неравенство:
1) 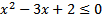 2)
2) 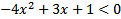 3)
3) 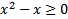
4) 2 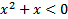 5)
5) 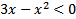 6)
6) 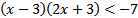
7) 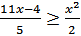
Задание 2. Решите неравенство:
1) 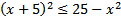 2)
2) 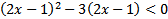
3) 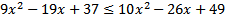 4)
4) 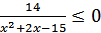 5)
5) 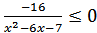
Задание 3. Устно
1) Решение какого из данных неравенств изображено на рисунке?

| ||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||
2) Укажите неравенство, которое не имеет решений.
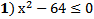
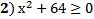
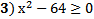
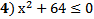
| ||||||||||||||||||||||||||||||||||||||||||||
3) Укажите неравенство, решением которого является любое число.
1) 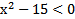 2)
2) 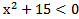 3)
3) 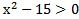 4)
4) 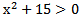
|
Задание 4. Решите неравенство:
1) 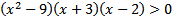 2)
2) 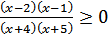 3)
3) 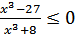
Самостоятельная работа
№1. На каком рисунке изображено множество решений неравенства
| |||||||||||||
| |||||||||||||
|
| |||||||||||||