2,13; 0,50; 13,63; 15,800; 0,500, 223,0; 2,130
05.04. 6 класс Математика Урок№ 9
Тема: «Сложение и вычитание десятичных дробей»
Здравствуйте, ребята.
Запишите число, классная работа.
Пятое апреля
Классная работа
Тема нашего урока: Сложение и вычитание десятичных дробей
Сегодня на уроке мы должны выяснить чего мы не знаем и найти самостоятельно выход из затруднения.
− Чтобы узнать что-то новое, что надо сделать сначала? (Повторить те знания, которые нам понадобятся на уроке.)
Посмотрите на цифры и кажите, что вы знаете об этих числах:
2,13; 0,50; 13,63; 15,800; 0,500, 223,0; 2,130
Прочитайте десятичные дроби.
Назовите целые и дробные части.
Какие дроби можно записать короче?
Назовите равные дроби.
Что мы еще умеем делать с десятичными дробями?
Сравните дроби: 3,6 и 3,15; 5,31 и 5,127; 0,713 и 0,8
- Каким алгоритмом мы пользуемся при сравнении двух десятичных дробей?
Уравнять число знаков после запятой, приписав к одной из них справа нули.
Отбросив запятую, сравнить получившиеся натуральные числа.
Изучение нового материала
Сложение десятичных дробей
Мы знаем, что десятичная дробь состоит из целой и дробной части. При сложении десятичных дробей нужно отдельно сложить каждую часть. Рассмотрим пример сложения 3,2 и 5,3. Для удобства используем метод столбика. Запишем эти две дроби в столбик. При этом целая часть одной дроби должна быть под целой частью другой. В школе это называют «запятая под запятой». Вот так:
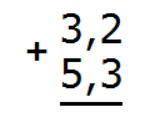
Складываем дробные части: 2 + 3 = 5. Запишем пятерку в дробной части ответа
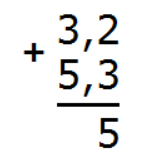
Теперь целые части: 3 + 5 = 8. Запишем восьмерку в целой части ответа:
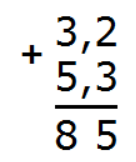
Отделим запятой целую часть от дробной, чтобы запятая была под запятой:
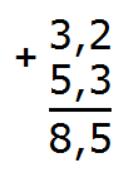
Получили ответ: 3,2 + 5,3 = 8,5.
Физкультминутка

Вычитание десятичных дробей
Процесс вычитания десятичных дробей очень похож на сложение. Будем использовать те же правила: «запятая под запятой» и «равное количество цифр после запятой».
Пример 1. Найти значение выражения 2,5 − 2,2
Запишем в столбик выражение так, чтобы запятая была под запятой:
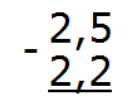
Вычислим дробную часть 5 − 2 = 3. Запишем тройку в десятой части ответа
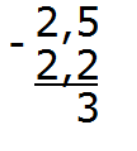
Вычислим целую часть 2 − 2 = 0. Запишем ноль в целой части ответа:
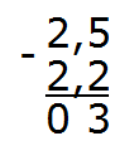
Отделим запятой целую часть от дробной:
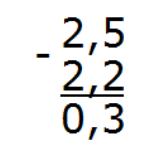
Вот и ответ: 2,5 − 2,2 = 0,3.
Пример 2. Вычислить: 7,353 – 3,1
В этом выражении разное количество цифр после запятой: в 7,353 три цифры после запятой, а в 3,1 только одна. Значит в дроби 3,1 в конце добавим два нуля, чтобы уравнять количество цифр в обеих дробях. То есть: 3,1 = 3,100.Запишем в столбик и посчитаем:
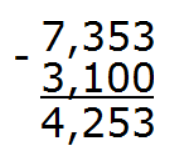
Ответ: 7,353 – 3,1 = 4,253.
Пример 3. Вычислить: 3 − 1,2
В этом примере из целого числа нужно вычесть десятичную дробь. Запишем это выражение столбиком так, чтобы целая часть десятичной дроби 1,23 была под числом 3. Вот так:
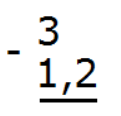
Сделаем количество цифр после запятой одинаковым:
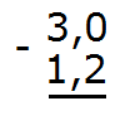
Теперь вычитаем десятые части: 0 − 2. От нуля невозможно вычесть число 2. Поэтому займем единицу у соседнего разряда. Таким образом 0 превращается в число 10. Вычисляем десятые части: 10 − 2 = 8. Запишем восьмерку в десятой части ответа:
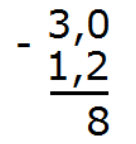
Сейчас вычтем целые части. В самом начале было число 3, но мы заняли у него единицу, поэтому оно обратилось в двойку. Поэтому: 2 − 1 = 1. Запишем единицу в целой части ответа:
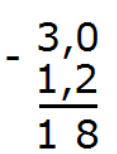
Отделим запятой целую часть от дробной:
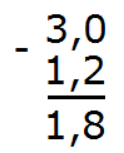
Ответ: 3 − 1,2 = 1,8.
Мы рассмотрели несколько примеров сложения и вычитания десятичных дробей. Чтобы каждый ученик в классе мог повторить эту последовательность, есть специальный алгоритм:
|
Проще говоря, правило сложения (вычитания) десятичных дробей звучит так: чтобы сложить (вычесть) две десятичные дроби, нужно записать их в столбик друг под другом, запятая под запятой. А потом сложить (вычесть) как обыкновенные числа и снести запятую.
Посмотрит ссылку:
https://youtu.be/rhuCCQRsrRU
Вычислим вместе 
Вычислите самостоятельно

Домашнее задание: изучить п. 4.3; выполнить упр. №759, 760, 761.








