Определение: Достоверным событием называется событие, которое наверняка произойдет в результате опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта.
Группа 7-18 Согласовано
Дата_03.04.2020 Зам. директора по УВР___________Татаринова В.Д
Урок № 90-91
Тема: Теория вероятностей. Сложение вероятностей.
http://matematikalegko.ru/veroyatnosti/slozhenie-i-umnozhenie-veroyatnostej.html
Ранее мы с вами уже разбирали некоторые задачи. Для их решения достаточно было знать формулу классической вероятности, то есть понятия благоприятных и всевозможных (равно-возможных) исходов, и применять немного простой «житейской» логики.
Есть задачи немного сложнее, для их решения необходимо знать и понимать: правило сложения вероятностей, правило умножения вероятностей, понятие – условная вероятность.
Немного теории:
Определение:
События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.
Классический пример: при бросании игральной кости (кубика) может выпасть только единица, либо только двойка, либо только тройка и т.д. Каждое из этих событий не совместно с другими и совершение одного из них исключает совершение другого (в одном испытании).
Определение:
События называются совместными, если появление одного из них не исключает появление другого.
Пример: из колоды карт будет взята дама и из колоды карт будет взята карта пик. Рассматриваются два события. Данные события не исключают друг друга — можно вытащить даму пик и, таким образом, произойдут оба события.
Есть ещё два определения (из основ теории вероятности):
Определение: Достоверным событием называется событие, которое наверняка произойдет в результате опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта.
Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие. Появление красного и появление зеленого шаров образуют полную группу событий.
Определение: События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.
О сумме вероятностей
Суммой двух событий А и В называется событие А+В, которое состоит в том, что наступит или событие А или событие В или оба одновременно.
Если происходят несовместные события А и В, то вероятность суммы данных событий равна сумме вероятностей событий:
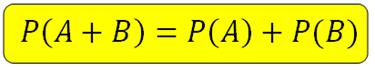 |
Пример с игральной костью:
Бросаем игральную кость. Какова вероятность выпадения числа меньшего четырёх?
Числа меньшие четырёх это 1,2,3. Мы знаем, что вероятность выпадения единицы равна 1/6, двойки 1/6, тройки 1/6. Это несовместные события. Можем применить правило сложения. Вероятность выпадения числа меньшего четырёх равна:
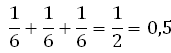
Действительно, если исходить из понятия классической вероятности: то число всевозможных исходов равно 6 (число всех граней кубика), число благоприятных исходов равно 3 (выпадение единицы, двойки или тройки). Искомая вероятность равна 3 к 6 или 3/6 = 0,5.
*Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без учёта их совместного появления: Р(А+В)=Р(А)+Р(В) -Р(АВ)
Задача 1
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 35 % этих стекол, вторая –– 65%. Первая фабрика выпускает 4% бракованных стекол, а вторая –– 2%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение. Первая фабрика выпускает 0,35 продукции (стёкол). Вероятность купить бракованное стекло с первой фабрики равна 0,04.
Вторая фабрика выпускает 0,65 стёкол. Вероятность купить бракованное стекло со второй фабрики равна 0,02.
Вероятность того, что стекло куплено на первой фабрике И при этом оно окажется бракованным равна 0,35∙0,04 = 0,0140.
Вероятность того, что стекло куплено на второй фабрике И при этом оно окажется бракованным равна 0,65∙0,02 = 0,0130.
Покупка в магазине бракованного стекла подразумевает, что оно (бракованное стекло) куплено ЛИБО с первой фабрики, ЛИБО со второй. Это несовместные события, то есть полученные вероятности складываем:
0,0140 + 0,0130 = 0,027
Ответ: 0,027
Задача 2
На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,3. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,25. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение
То есть необходимо найти вероятность того, что школьнику достанется вопрос ЛИБО по теме «Вписанная окружность», ЛИБО по теме «Параллелограмм». В данном случае вероятности суммируются, так как это события несовместные и произойти может любое из этих событий: 0,3 + 0,25 = 0,55.
*Несовместные события – это события, которые не могут произойти одновременно.
Ответ: 0,55
Задача 3
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,07 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение
Найдем вероятность того, что неисправны оба автомата.
Эти события независимые, значит вероятность будет равна произведению вероятностей этих событий: 0,07∙0,07 = 0,0049.
Значит, вероятность того, что исправны оба автомата или какой-то из них будет равна 1 – 0,0049 = 0,9951.
*Исправны оба и какой-то один полностью – отвечает условию «хотя бы один».
Можно представить вероятности всех (независимых) событий для проверки:
1. «неисправен-неисправен» 0,07∙0,07 = 0,0049
2. «исправен-неисправен» 0,93∙0,07 = 0,0651
3. «неисправен-исправен» 0,07∙0,93 = 0,0651
4. «исправен-исправен» 0,93∙0,93 = 0,8649
Чтобы определить вероятность того, что исправен хотя бы один автомат, необходимо сложить вероятности независимых событий 2,3 и 4:
0,0651 + 0,0651 + 0,8649 = 0,9951
Ответ: 0,9951






Домашнее задание
Задание. Конкурс исполнителей проводится в 5 дней. Всего заявлено 50 выступлений: по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 30 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность того, что выступление исполнителя из России состоится в третий день конкурса?
Ответы на выполненное задание (в файлах может быть текст, скриншоты, таблицы и т.д.) высылайте на электронный ящик преподавателя:
kacha _ s _ s @ mail . ru








