Задание 1. Определите, какие из данных предложений являются высказываниями. Оцените истинность высказываний.
Урок № 2
Информатика
29.03.2022
Тема. Логический тип данных. Логические величины. Логические операции. Правила записи и вычисления логических выражений.
-Здравствуйте, ребята. Давайте настроимся на хорошую работу, сегодня мы будем изучать тему «Логические величины и выражения».
-Запишите в тетради число 29 марта, слова классная работа и тему урока.
В 9 классе вы уже знакомились с некоторыми логическими операциями и таблицами истинности для них. Сегодня мы повторим то, что вы уже изучали и рассмотрим несколько новых операций.
Давайте запишем определения, с которыми будем работать в дальнейшем.
Логическое высказывание – это повествовательное предложение, про которое можно однозначно сказать, истинно оно или ложно.
Логическое выражение – это символическая запись высказывания, которая может содержать логические переменные и знаки логических операций.
Рассмотрим следующие предложения:
- Клавиатура предназначена для ввода текстовой информации и команд управления компьютером.
- При приёме информации происходит процесс переноса информации от источника к приёмнику.
Эти предложения будут относится к высказываниям, так как можно точно сказать истины они или ложны. Первое высказывание является истинным, а второе – ложным. А вот следующие предложения:
- Который час?
- Не поднимай телефон!
Не являются высказываниями, так как в определении сказано, что высказывание – это повествовательно предложение.
Для построения высказываний могут использоваться знаки различных формальных языков: математики, физики, химии и других.
Числовые выражения не являются высказываниями. Но, в то же время, если из двух выражений составить одно и соединить их знаком равенства или неравенства, то новое выражение будет высказыванием.
Логические высказывания бывают простыми и составными.
Простое высказывание – это высказывание, в котором никакая его часть сама не является высказыванием.
Сложное или же составное высказывание – это высказывание, которое строится из простых с помощью логических операций.
Логические величины – это понятия, выражаемые словами Истина (True), Ложь (False). Истинность высказывания выражается через логические величины.
Логическая переменная – это символически обозначенная логическая величина. То есть логическая величина может обозначаться, например, буквой латинского алфавита. Сама же буква будет являться переменной логической величины. В свою очередь, она может принимать только значение Истина или Ложь.
Задание 1. Определите, какие из данных предложений являются высказываниями. Оцените истинность высказываний.
| Обязательно вымой за собой посуду. | |
| Переводчик должен знать хотя бы два языка. | |
| Ты любишь смотреть футбол? | |
| Пять меньше семи. | |
| Земля – самая большая планета Солнечной системы. | |
| Каждый треугольник является равносторонним. | |
| В феврале всегда 28 дней. | |
| А ведь хорошо, что сейчас весна! |
Как вы уже знаете, логические операции делятся на две группы: унарные и бинарные.
Унарные – операции, которые выполняются над одной величиной. Такой операцией является инверсия/отрицание (логическое НЕ).
Запись: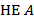 
, 
, 
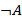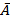
В языках программирования Pascal, Python: not A.
Таблица истинности:
| A | НЕ А |
| 0 | 1 |
| 1 | 0 |
Операция НЕ обладает свойством обратимости: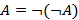 
. Если её применить дважды, мы восстановим исходное значение.
Бинарные – операции, которые выполняются над двумя величинами.
Конъюнкция (И, логическое умножение).
Запись: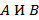 
, 
, 
, 
.
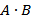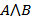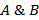В языках программирования Pascal, Python: A and B.
Таблица истинности:
| A | B |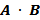 
|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Дизъюнкция (ИЛИ, логическое сложение).
Запись: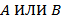 
, 
, 
.
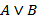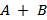В языках программирования Pascal, Python: A or B.
Таблица истинности:
| A | B |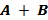 
|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Данные операции (НЕ, И, ИЛИ) образуют базис: их достаточно для того, чтобы с их помощью записать любую логическую операцию.
Исключающее ИЛИ («либо… , либо…»).
Запись: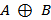 
.
Выражение через базовые: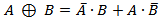 
.
Таблица истинности:
| A | B |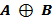 
|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Операция исключающее ИЛИ так же обладает свойством обратимости: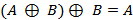 
.
Импликация(«если… , то»).
Запись: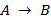 
.
Выражение через базовые: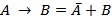 
Таблица истинности:
| A | B |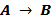 
|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Эквиваленция(«тогда и только тогда»).
Запись: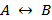 
.
Выражение через базовые: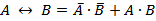 
.
Таблица истинности:
| A | B |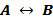 
|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Давайте составим таблицу истинности для всех логических операций. В ней И – это истина, Л – Ложь.
В первых двух столбцах предоставлены всевозможные исходные данные А и B.
В третьем столбце будет идти А.
Как мы с вами знаем, из определения операция отрицания преобразует исходное выражение в новое, значение которого противоположно исходному. То есть, если А было истинно, при отрицании оно станет ложным. И наоборот, если выражение было ложным, то оно станет истинным. Заполним третий столбец таблицы исходя из данных первого.
Далее идёт конъюнкция. Здесь мы будем смотреть на значения, которые принимают выражения А и B. Мы с вами знаем, что при конъюнкции новое высказывание будет являться ложным тогда, когда хотя бы одно из исходных высказываний ложно. То есть, исходя из данных нашей таблицы, в первой строке оба высказывания истины, значит и новое будет истинно. А вот все остальные будут ложными, так как во второй строке ложно высказывание B, в третьей – А, а в четвёртой – оба.
И последний, пятый столбец – дизъюнкция. Снова будем брать значения выражений А и B. Новое высказывание будет истинным тогда, когда хотя бы одно исходное высказывание истинно. Значит в первых трёх строках 5 столбца новые выражения будут истинны, так как в первой строке истинны оба высказывания А и B, во второй – А, в третьей – B. А вот в четвёртой строке мы можем видеть, что значения А и B оба ложны, значит и новое выражение будет ложно.
Логическая формула – это формула, которая содержит только логические величины и знаки логических операций. Результатом вычисления такой формулы будет являться истина или ложь.
Но также стоит помнить, что операции в скобках выполняются в первую очередь. Если же у нас идут несколько равнозначных операций подряд, то выполнение их будет происходить слева направо.
Давайте разберёмся на примере.