Задание № 11. Ифы с неограниченными альтернативами
Инструкция (варианты происшествий описаны выше) «Мы поиграем в игру, где ты будешь задавать мне вопро сы, а я тебе буду отвечать. Я расскажу о каком-нибудь происшествии, а твоей задачей будет установить, как оно произошло, задавая мне такие вопросы, чтобы я смогла ответить на них только «да» или «нет». Например, в первой игре я тебе сообщаю: «Мальчик пришел домой из школы в середине занятий». А ты определи, как это получилось, спрашивая меня и задавая мне различные вопросы. Но я могу отвечать только двумя словами: «да» и «нет». Если твой вопрос окажется неясным или я не смогу на него ответить и скажу: «Я не могу ответить», — ты попытай
ся сказать по-другому, или
Рис. 37, 38
объясни свой вопрос, или задай другой. Цель игры состоит в том, чтобы найти ответ с помощью наименьшего возможного числа вопросов, хотя ты и можешь задавать их столько, сколько тебе понадобится. Если ты поймешь, что не можешь найти причину, то можешь сдаваться, но не делай этого раньше, чем попытаешься найти правильный ответ»*.
В конце эксперимента детей просили описать, как они играли в игру. Была ли у них какая-нибудь система для получения ответов? Считают ли они, что вопросы какого-нибудь одного определенного рода лучше других в том отношении, что позволяют получить ответ быстрее всего?
Спрашивали о том, какой вопрос они предпочли бы задать в начале игры: «С человеком что-то было неладно?» или «У него был сердечный приступ?»
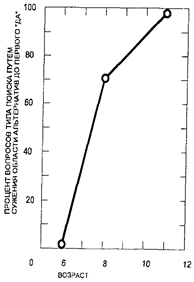
Возрастные различия выступают особенно отчетливо при подсчете количества детей, обнаруживающих хоть какую-то последовательность в постановке вопросов и в использовании полученных ранее ответов для формулировки новых вопросов. На рис. 39 видно закономерное возрастание этой способности детей от 6 до 11 лет.
Осознание стратегии при игре в «Девятнадцать вопросов» появляется только в 8 лет — в том самом возрасте, когда появляется четкое осознание своего «я» как постоянной точки опоры и отсчета. Сужение рамок поиска, предшествующее опробованию вероятности разных причин, — это еще один шаг вперед. Все эти три процесса — сужение, оценка и конкретизация — входят друг в друга, как матрешки. Ведь если опробуешь ряд конкретных альтернатив, необходимо оценить, насколько они вероятны.
Задание № 12
Эксперимент на исследование понимания детьми принципа сохранения количества жидкого вещества (рис. 40).
В этом эксперименте маленькому ребенку показывали два стакана и просили налить в каждый поровну подкрашенной воды. После того как ребенок проделал это, воду из одного стакана переливали в сосуд иной формы и ре-
* Мальчику надо было к зубному врачу. В задаче с дорожным происшествием ответ — человек ехал поздно и заснул за рулем.
204
бенка спрашивали, осталось ли неизменным количество воды.
Ж. Пиаже объяснял эти факты с помощью логической метатеории. Объяснение состоит в том, что переход от непонимания детьми принципа сохранения количества вещества к его пониманию представляет собой коренной переворот, знаменует конец до-операциональной фазы мышления и начало фазы конкретных операций.
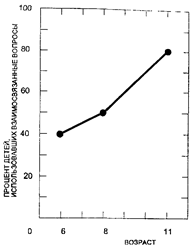
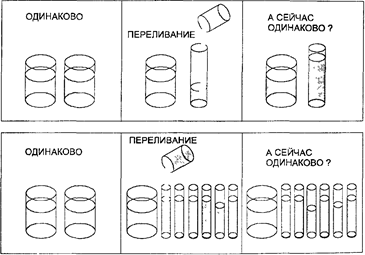
Рис. 39,40
Для этого периода характерно превращение внешне развернутых операций в интериоризированные. Главной особенностью интериоризированных конкретных операций является их обратимость: ребенок способен не только произвести в уме операцию, но также и осуществить ее в противоположном направлении, обратить.
205
Задание № 13
Эксперимент перцептивное экранирование (рис. 41). Вначале всех детей провели через предварительный опыт, описанный выше. Далее происходил следующий эксперимент. Применялось четыре пары стаканов; в каждой паре один стакан был стандартным, а другой отличался от него, как это показано на рис. 45. Затем стаканы помещали за ширму размером 12 х 5 дюймов так, что поверх нее виднелись только их вершины. Воду из стандартного стакана переливали во второй, а испытуемого просили ответить, осталось ли количество воды тем же самым, и объяснить свой ответ: Экран не убирали, так что ребенок не мог видеть уровень воды во втором стакане. Пары стаканов всегда предъявлялись в фиксированном порядке (а, в, с, d).
Во второй части эксперимента испытуемому снова показывали пары стаканов в том же порядке, что и перед этим. Однако на этот раз экран отсутствовал, и ребенка просили сказать, будет ли во втором стакане столько же воды, сколько сейчас в стандартном, если ее перельют из первого сосуда во второй. Его просили также показать пальцем уровень, до которого поднимется вода во втором стакане, когда ее туда перельют. В этой части эксперимента детей снова просили объяснить свои ответы. Переливания
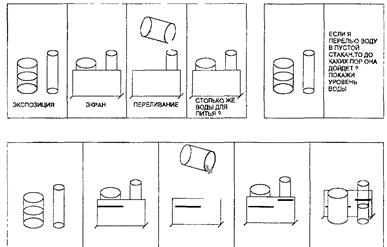
а &д
Рис. 41
206
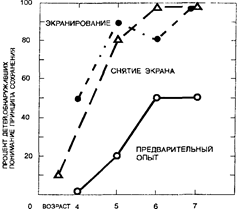
Рис.42
воды никогда не производили, так что испытуемые не видели, на каком уровне она устанавливается во втором стакане.
В третьей части эксперимента пары стаканов в прежнем порядке предъявляли перед экраном. Ребенка просили показать на экране уровень воды в стандартном стакане. Затем, как и в первой части эксперимента, стаканы помещали позади экрана, переливали воду из стандартного стакана во второй и просили ребенка ответить, осталось ли количество воды во втором стакане прежним. Его просили также нарисовать вторую линию, обозначающую уровень воды во втором стакане, используя в качестве опоры линию, проведенную им ранее по отношению к стандартному стакану. Затем экран убирали.
В первый раз за все опыты с экраном ребенок мог увидеть воду во втором стакане. В этот момент ему предлагали высказать суждение о том, сохранилось ли то количество воды, что было до переливания, и обосновать свой ответ.
Наконец, проводили заключительный опыт, повторявший предварительный, схематически изображенный на рис. 41. Результаты экспериментов представлены на рис. 42 и 43.
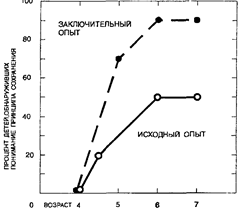
Рис.43
207
Упражнение оказало заметное влияние на действия всех детей, кроме четырехлеток. Почти удвоилось число правильных ответов у детей 6 и 7 лет. Экран как бы «заставляет» класть в основу суждения соображения о тождестве.
Ребенку можно помочь преодолеть отделяющий его от понимания истины разрыв, экранировав от восприятия ситуации и поощряя его попытки использовать для кодирования своих суждений и обоснований в опытах с экраном языковые выражения, подчеркивающие непрерывность существования вещества, — другими словами, формулировку тождества. Пройдя подобную тренировку, ребенок становится чувствительным к конфликту, существующему иногда между «видимостью» и «действительным положением». «Видимость» выражается в наглядных представлениях, а «действительное положение» — в символических образах.
Здесь мы сталкиваемся с проблемой установления соответствия между языком ребенка и его способом организации непосредственного опыта, к которому этот язык должен быть приложен. У детей еще не сформировалась структура, позволяющая им относиться к перцептивному тождеству так, чтобы это не мешало им использовать усложненные формы языка вполне адекватным способом.
Задание № 14
Эксперимент: понимание детьми принципа сохранения количества твердого вещества.
Опыты проводились индивидуально в течение единственного сеанса продолжительностью 30 — 45 минут.
Предварительный и заключительный опыты. Ребенку показывали два шарика из пластилина и спрашивали, поровну ли в них материала. Если ребенок считал, что шарики неодинаковые, их делали для него «такими же самыми» с помощью любых указанных ребенком операций. Когда ребенок наконец заявлял, что оба шарика «такие же самые», экспериментатор превращал один из них в «сосиску», а ребенок наблюдал за его действиями. Наконец, испытуемого спрашивали, содержат ли сосиска и шарик одинаковое количество материала или же в одном из них материала больше. Если ребенок утверждал, что в шарике и сосиске одинаковое количество материала, и адекватно обосновывал свой опыт, его исключали из дальнейших опытов.
В заключительных опытах снова проверялась уверенность этих детей в своих суждениях, и научение считалось фак-
208
том только в том случае, если на этот раз испытуемый настаивал на правильном ответе, несмотря на вызов, брошенный ему экспериментатором.
Заключительный опыт был тождествен с предварительным, с тем исключением, что испытуемый делал из шарика «змею» или «веревку» много длиннее «сосиски» из предварительного опыта.
Упражнение состояло из ряда последовательных проб, в ходе которых форма одного из шариков (ребенок заявлял, что он «такой же», как и второй шарик) изменялась, а потом восстанавливалась.
Ребенка просили высказать суждение о количестве материала, когда шарику придавали новую форму, когда снова восстанавливали его форму, когда ту же новую форму придавали второму шарику и когда он принимал прежний вид.
...Во всех условиях упражнений, за исключением указанного, в конце пробы от ребенка приходится получать еще одно суждение для того, чтобы убедиться, что перед следующей пробой ребенок воспринимает шарики как одинаковые.
Упражнение проводилось в виде:
1) манипулирования — ребенку самому разрешали менять форму кусков,
2) экранирования — в ходе пробы один из шариков пластилина прятали под чашкой, а другому в это время придавали какую-нибудь другую форму. Как только изменение формы одного шарика заканчивалось, его прятали под чашку и ребенка просили высказать свое мнение относительно того, сколько материала содержалось в каждом кусочке. Для того чтобы восстановить форму первого шарика, его вынимали из-под чашки; таким образом, когда ребенка просили во второй раз высказаться о количестве материала в шарике, он мог видеть только один комочек глины, а другой (стандартный) был в это время скрыт под чашкой. Когда стандарт открывали, от ребенка требовали высказать третье суждение, чтобы перед третьей пробой он был уверен в том, что оба шарика снова «одни и те же».
Словесное обозначение. Разницу между упражнениями со словесным обозначением и без него лучше всего можно понять из конкретного описания.
После того как испытуемый делал карандаш (или что ему еще хотелось) из одного шарика и высказывал свое суждение о количестве материала в двух шариках, экспериментатор говорил ему: «Хорошо, а теперь, пожалуй-
209
ста, возьми карандаш, который ты сделал, и преврати его снова в шарик, в точности такой, какой он был раньше» (выделенная часть фразы неизменно акцентировалась). Когда ребенок делал из карандаша шарик, экспериментатор несколько раз спрашивал его: «Теперь он такой же, какой был и раньше?» Когда испытуемый наконец отвечал на этот вопрос утвердительно, его снова просили высказать свое суждение о количестве материала в двух кусках пластилина.
Результаты показывают, что только если ребенок и говорит, и делает, он научается не полагаться целиком на то, что видит. Научение может произойти только тогда, когда представления разной модальности взаимодействуют друг с другом (рис. 44).
100
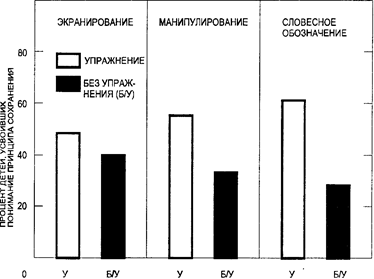
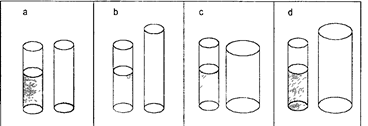
Рис. 44, 45
210
Не исключено, чго психология понимания принципа сохранения количества вещества (в отличие от так называемой логики этой проблемы) состоит в осознании того факта, что вещь может рядиться в самые разные одежды и все же оставаться той же самой вещью. Один ребенок может открыть эту мысль с помощью действия, используя разными способами и для разных целей одну и ту же палочку, другой — символическим путем, с помощью таких мощных средств, как перефразирование и изменение словесных обозначений. Восприятие же и наглядные представления чаще всего приводят к ошибочному истолкованию изменения видимых признаков вещи как изменения ее тождества.








