3. Контрольные задания по дисциплине «Надежность технических систем и техногенный риск»
3.1. Определение надежности объекта
В период нормальной эксплуатации постоянные отказы не проявляются, и надёжность характеризуется внезапными отказами. Эти отказы вызываются неблагоприятным стечением многих обстоятельств и поэтому имеют постоянную интенсивность, которая не зависит от возраста изделия:
λ(t) = λ = cоnst,
где λ = 1/mt; m t – средняя наработка до отказа (обычно в часах).
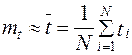 .
.
Здесь t – наработка до отказа i -го изделия; N – общее число наблюдений. Тогда λ выражается числом отказов в час и, как правило, составляет малую величину.
Вероятность безотказной работы
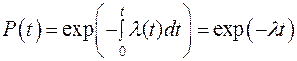 .
.
Она подчиняется экспоненциальному закону распределения времени безотказной работы и одинакова в любых одинаковых промежутках времени в период нормальной эксплуатации.
Если работа изделия происходит при разных режимах, а следовательно, и интенсивностях отказов λ j, то
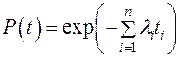 .
.
Задание 1
Определить в соответствии с вариантом (табл. 3.1) один из показателей надежности (вероятность безотказной работы P(t), время безотказной работы t или интенсивность отказов λ в период нормальной эксплуатации).
Таблица 3.1
Задачи по определению надежности объекта
| № варианта | Содержание задачи |
| 1 | Определить время безотказной работы токарного станка при заданной вероятности безотказности 0,88 и интенсивности отказов кинематических пар станка, равной 3 · 10– 5 ч–1 |
| 2 | Для протяжного станка задан гамма-процентный ресурс ТГ = 99 %, определить необходимый показатель интенсивности отказов λ с уче- том заданного времени эксплуатации, равного 12 000 ч |
| 3 | Питание цехового электрического трансформатора осуществляется кабелем, определить надёжность его против обрыва после эксплуатации на протяжении 5000 ч (λ = 3 · 10 – 6 ч –1) |
| 4 | Для электродвигателя вентилятора местной вытяжной вентиляции машины литья под давлением установлено время безотказной работы t = 2000 ч, определить P ( t ) (λ = 3 · 10– 4 ч–1) |
| 5 | Определить P ( t ) концевого выключателя строгального станка при заданном времени безотказной работы в 5000 ч (λ = 3 · 10– 4 ч–1) |
| 6 | Для автоматического выключателя электроэрозионного станка установлена P ( t ) = 0,9999, определить время безотказной работы (λ = 1 · 10– 3 ч–1) |
| 7 | Для транспортной машины задан гамма-процентный ресурс T Г = 99,95 %, который должен иметь место на протяжении 5 000 ч эксплуатации, определить соответствующую ему интенсивность отказов λ |
| 8 | Сцепление валов в машинах обеспечивается муфтами сцепления, при наработке 1200 ч определить их P ( t ) (λ = 4 · 10– 6 ч–1) |
| 9 | Определить время безотказной работы предохранительного клапана гидросистемы станка при заданной P ( t ) = 0,98 (λ = 1 · 10–5 ч–1) |
| 10 | Ограничители передвижений предупреждают аварийные ситуации, определить P ( t ) для них после работы в течение 14 000 ч (λ =1,65 · 10– 7 ч–1) |
| 11 | Пневматические цилиндры являются основными элементами пневмосистем встряхивающих формовочных машин, определить время работы, после которого P ( t ) составит 0,8 (λ = 2 · 10– 9 ч–1) |
| 12 | Время разгерметизации гидросистемы (утечки) из-за выхода из строя прокладок равно интервалу в 1500 ч, определить P ( t ) трубопроводов (λ = 1 · 10– 8 ч–1) |
| 13 | Насос гидропанели радиально-сверлильного станка рассчитан на вероятность безотказности P ( t ) = 0,95, определить соответствующее время безотказной работы (λ = 3 · 10– 5 ч–1) |
Окончание табл. 3.1
| № варианта | Содержание задачи |
| 14 | Определить показатели надёжности зажима токарного станка, удерживающего обрабатываемую заготовку, через 1000 ч эксплуатации (λ = 4 ּ 10 - 9 ч -1). |
| 15 | Для обеспечения точного исполнения циклов технологических процессов эксцентрики механических систем должны иметь высокую надежность, определить их P ( t ) после работы в течение 3000 ч (λ = 1 · 10–9 ч–1) |
| 16 | Предохранители главного движения машин исключают аварии, определить время безотказной работы их при P ( t ) = 0,999 (λ = 1 · 10–6 ч–1) |
| 17 | Определить показатели надежности шариковых подшипников после 14 000 ч работы (λ = 7,2 · 10–8 ч–1) |
| 18 | Питание цехового электрического трансформатора осуществляется кабелем, определить надёжность его против обрыва после эксплуатации на протяжении 9000 ч (λ = 3 · 10–6 ч–1) |
| 19 | Определить P ( t ) концевого выключателя строгального станка при заданной безотказной работе в 8 000 ч (λ = 3 · 10–4 ч–1) |
| 20 | Сцепление валов в машинах обеспечивается муфтами сцепления, при наработке 18 000 ч определить их P ( t ) (λ = 4 · 10–6 ч–1) |
3.2. Структурно-логический анализ технических систем.
Расчет вероятности безотказной работы систем
Большинство технических объектов являются сложными системами, состоящими из отдельных узлов, деталей, агрегатов, устройств контроля, управления и т. д. Техническая система (ТС) – совокупность технических устройств (элементов), предназначенных для выполнения определенной функции или функций. При составлении структурной схемы придерживаются следующих правил:
1) элементы изображаются в виде прямоугольников и обозначаются номерами или индексами 1 (а);
2) одна сторона прямоугольника считается входом, другая – выходом для сигнала;
3) элемент считается работоспособным, если сигнал со входа элемента проходит на выход;
4) отказ элемента делает невозможным прохождение сигнала;
5) линии, соединяющие элементы друг с другом, считаются абсолютно безотказными.
Выполняется деление объекта на элементы (системы):
1) по принципу действия (механическая часть, электрическая часть, гидравлическая часть и др.);
2) по характеру выполняемых работ;
3) по операциям, выполняемым машиной в течение цикла.
Степень деления может быть разной. Для расчета и оценки критериев надежности подсистем достаточным будет их представление в виде отдельных сборочных единиц (корпус, вентилятор, воздуховод и т. п.).
Если же поставленная задача включает оптимизацию конструкции отдельных элементов, то деление должно быть более глубоким и доходить до уровня отдельных деталей.
Правила соединения элементов:
1) если отказ элемента приводит к отказу всего объекта, то элемент считается встроенным в структурную схему последовательно (рис. 3.1);
2) если отказ элемента не приводит к отказу всего объекта, то элемент считается встроенным в структурную схему параллельно (рис. 3.2).
 |

 |
Работоспособность последовательной системы обеспечивается при условии, когда все n элементов системы находятся в работоспособном состоянии.
Безотказность работы i-го элемента зависит от безотказности других:
Рс(t) = Р1(t) · Р2(t) · … · Р i(t) ·… ·Р n(t) = 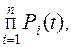 (3.1)
(3.1)
Q с(t) = 1 – Рс(t) =1 – 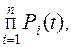 (3.2)
(3.2)
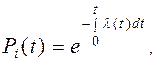
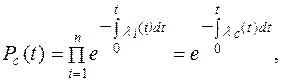 (3.3)
(3.3)
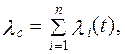 (3.4)
(3.4)
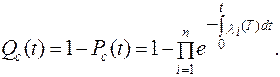 (3.5)
(3.5)
Отказ параллельной системы произойдёт при отказе всех элементов.
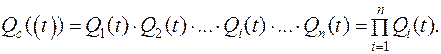 (3.6)
(3.6)
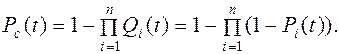 (3.7)
(3.7)
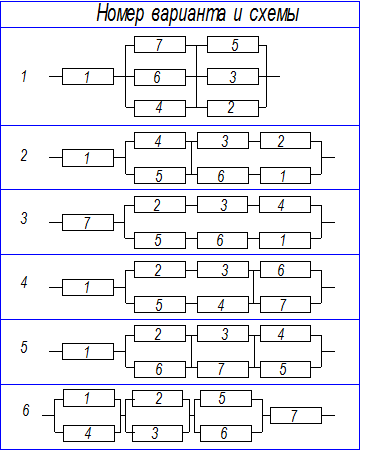
Задание 2
Зная значения надежности составных элементов, вычислить вероятность безотказной работы системы. Ответить на вопрос: надежна ли данная система. Предложить мероприятия по увеличению надежности, рассчитать систему с резервным элементом.

| Элемент | Вероятность безотказной работы Р | ||
| Вариант | |||
| 1 | 2 | 3 | |
| Первый | 0,45 | 0,75 | 0,9 |
| Второй | 0,65 | 0,6 | 0,95 |
| Третий | 0,9 | 0,7 | 0,2 |
| Четвертый | 0,3 | 0,85 | 0,8 |
| Пятый | 0,9 | 0,8 | 0,7 |
| Шестой | 0,9 | 0,9 | 0,6 |
| Седьмой | 0,95 | 0,55 | 0,75 |
| Восьмой (резервный) | 0,95 | 0,9 | 0,9 |
3.3. Расчет вероятности безотказной работы
сложных систем
На практике встречаются системы, для описания которых параллельное или последовательное соединение не годится. Рассмотрим в качестве примера систему, изображённую на рис. 3.3.
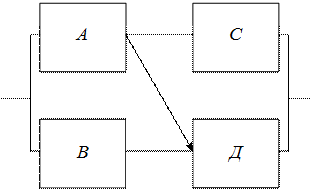
Рис. 3.3. Система со сложным соединением элементов
В данной системе отказ элемента А нарушает сразу два пути – АС и АД. Таким образом, это соединение не является параллельным. Последовательным такое соединение назвать также нельзя: в случае отказа элемента С система остаётся работоспособной.
Для определения вероятности безотказной работы системы или надёжности её функционирования используют несколько методов. Здесь принят метод прямого перебора. Метод состоит в том, что рассматриваются все возможные способы появления отказов, т. е. не отказал ни один элемент, отказал один элемент, два и т. д.
В системе, изображённой на рис. 3.3, элементы имеют следующие вероятности безотказной работы:
Р(А) = 0,9; Р(В) = 0,8;
Р(С) = 0,6; Р(Д) = 0,7.
Здесь А – событие «элемент А работает безотказно»; тогда Ā – событие «элемент А отказал». Аналогично определяются события для всех остальных элементов. Затем вычисляется вероятность состояния системы для каждого способа появления отказа. Результаты записываются в табл. 3.2.
Таблица 3.2
Расчет надежности
| Состояние системы | Число отказавших элементов | Событие, характеризующее состояние системы | Вероятность состояния системы | Отметка о работоспособности системы, изображённой на рис. 3.3 |
| 1 | 0 | 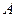 ∩ ∩ 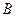 ∩ ∩ 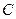 ∩ ∩ 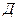
| 0,3024 | + |
| 2 | 1 | 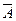 ∩ ∩ 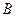 ∩ ∩ 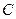 ∩ ∩ 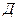
| 0,0336 | + |
| 3 | 1 | 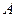 ∩ ∩ 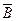 ∩ ∩ 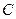 ∩ ∩ 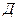
| 0,0756 | + |
| 4 | 1 | 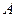 ∩ ∩ 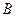 ∩ ∩ 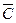 ∩ ∩ 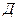
| 0,1295 | + |
| 5 | 1 | 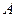 ∩ ∩ 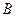 ∩ ∩ 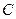 ∩ ∩ 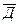
| 0,2016 | + |
| 6 | 2 | 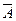 ∩ ∩ 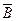 ∩ ∩ 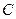 ∩ ∩ 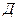
| 0,0084 | – |
| 7 | 2 | 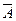 ∩ ∩ 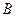 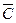 ∩ ∩ 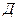
| 0,0144 | + |
| 8 | 2 | 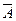 ∩ ∩ 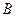 ∩ ∩ 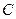 ∩ ∩ 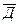
| 0,0224 | – |
| 9 | 2 | 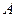 ∩ ∩ 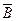 ∩ ∩ 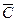 ∩ ∩ 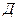
| 0,0324 | + |
| 10 | 2 | 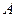 ∩ ∩ 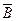 ∩ ∩ 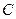 ∩ ∩ 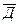
| 0,0504 | + |
| 11 | 2 | 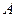 ∩ ∩ 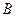 ∩ ∩ 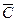 ∩ ∩ 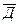
| 0,0864 | – |
| 12 | 3 | 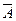 ∩ ∩ 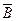 ∩ ∩ 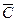 ∩ ∩ 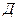
| 0,0036 | – |
| 13 | 3 | 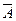 ∩ ∩ 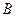 ∩ ∩ 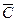 ∩ ∩ 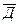
| 0,0096 | – |
| 14 | 3 | 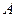 ∩ ∩ 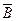 ∩ ∩ 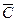 ∩ ∩ 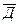
| 0,0056 | – |
| 15 | 3 | 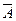 ∩ ∩ 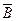 ∩ ∩ 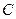 ∩ ∩ 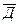
| 0,0216 | – |
| 16 | 4 | 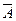 ∩ ∩ 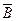 ∩ ∩ 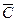 ∩ ∩ 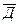
| 0,0024 | – |
| ∑ | 1,0000 | 0,8400 |
Таким образом, система со сложным соединением элементов (подсистем) имеет вероятность безотказной работы 0,84.
Задание 3
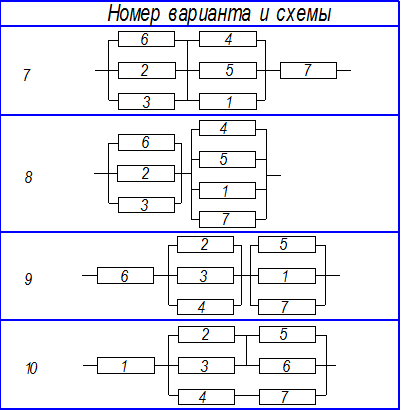
Рассчитать вероятность безотказной работы сложной системы для схем (рис. 3.4).
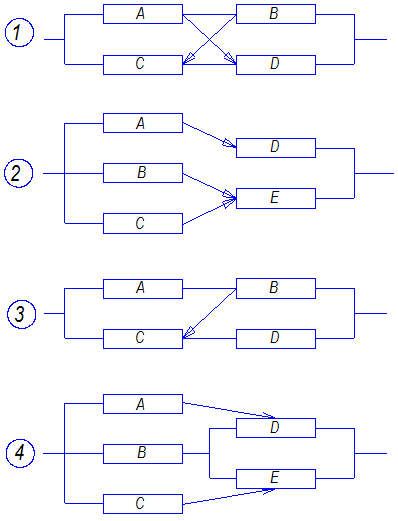
Рис. 3.4. Расчетные схемы
| Элемент | Вероятность безотказной работы P | |||||||
| Вариант | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| А | 0,5 | 0,9 | 0,6 | 0,9 | 0,7 | 0,8 | 0,6 | 0,7 |
| В | 0,9 | 0,5 | 0,9 | 0,8 | 0,8 | 0,9 | 0,7 | 0,3 |
| С | 0,8 | 0,6 | 0,8 | 0,7 | 0,9 | 0,7 | 0,8 | 0,9 |
| D | 0,7 | 0,7 | 0,5 | 0,5 | 0,8 | 0,6 | 0,9 | 0,5 |
| Е | 0,6 | 0,8 | 0,8 | 0,7 | 0,8 | 0,5 | 0,9 | 0,6 |
3.4. Анализ и расчет надежности, расчёт риска объекта
методами «дерева неисправностей» и «дерева рисков»
Анализ и расчет надежности, расчет риска проводится на основе анализа причинно-следственных связей «дерева неисправностей» с последующим расчётом вероятности отказа, вероятности безотказной работы объекта и риска.
Для определения причин возникновения отказов на производственном оборудовании применяется метод «дерева неисправностей». Он заключается в построении и анализе модели надежности, представляющей собой логико-вероятностную модель причинно-следственных связей отказов объекта с отказами его элементов и другими событиями.
Последовательность построения «дерева неисправностей» описана в
гл. 8 первой части данного учебного пособия и состоит в осуществлении анализа сверху вниз. Для наглядного представления причинной взаимосвязи с помощью «дерева неисправностей» используется два типа элементарных блоков: логические символы (табл. 8.1) и символы событий (табл. 8.2). Логические символы связывают события в соответствии с их причинными взаимосвязями.
3.4.1. Расчетные формулы
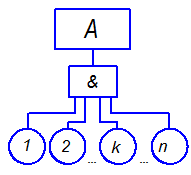
При расчетах вероятности события, объединенные условием «И», перемножаются. Вероятность события А в зависимости от исходных событий
1, 2,…, n, вероятности которых Р1, Р2, … , Р n (рис. 3.5), будет определяться по формуле
РА = Р1· Р2 · …· Рn = 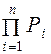 . (3.8)
. (3.8)
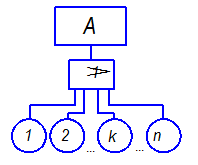
Вероятность события А в зависимости от исходных событий, соединенных символом «ИЛИ» (рис. 3.6), определяется по формуле
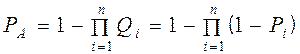 . (3.9.)
. (3.9.)
В частности, при n = 2 выражение (3.9) преобразуется к виду
РА = Р1 + Р2 – Р1 · Р2 ,
при n = 3 – к виду
РА = Р1 + Р2 + Р3 – Р1 · Р2 – Р3 · Р1 – Р2 · Р3 + Р1 · Р2 · Р3.
 |
Приведен пример анализа надежности станка сверлильно-расточной группы, выполненного согласно предлагаемой методике (см. п. 3.4.3). Для получения более полного представления о системе «станок» необходимо пользоваться его описанием.
Устройство и принцип работы всех типов металлообрабатыващих станков (токарных, фрезерных, строгальных, шлифовальных и др.) практически не имеют различий. Но станки различаются по назначению, конструкциям, размерам и т. д. В состав технической системы «станок» входят механическая, электрическая, могут входить гидравлическая, пневматическая подсистемы, а также система управления. Для анализа надежности других станков можно пользоваться приведенным примером.
3.4.2. Описание системы
«станок сверлильно-расточной группы»
Сверлильные станки предназначены для сверления отверстий, нарезания в них резьбы метчиком, растачивания и притирки отверстий, вырезания дисков из листового материала и т. д. Эти операции выполняют сверлами, зенкерами, развертками и другими подобными инструментами. Существует несколько типов универсальных сверлильных станков.
Одношпиндельные настольно-сверлильные станки используют для обработки отверстий малого диаметра. Станки широко применяют в приборостроении. Шпиндели этих станков вращаются с большой частотой.
Вертикально-сверлильные станки (основной и наиболее распространенный тип) применяют преимущественно для обработки отверстий в деталях сравнительно небольшого размера. Для совмещения осей предусмотрено перемещение заготовки относительно инструмента.
Радиально-сверлильные станки используют для сверления отверстий в деталях больших размеров. На этих станках совмещение осей отверстий и инструмента достигается перемещением шпинделя станка относительно неподвижной детали.
Многошпиндельные сверлильные станки обеспечивают значительное
повышение производительности труда по сравнению с одношпиндельными станками.
Горизонтально-сверлильные станки предназначены для глубокого сверления.
К группе сверлильных станков можно также отнести центровальные станки, которые служат для получения в торцах заготовок центровых отверстий.
Основными размерами сверлильных станков являются наибольший условный диаметр сверления, размер конуса шпинделя, вылет шпинделя, наибольший ход шпинделя, наибольшие расстояния от торца шпинделя до стола и до фундаментной плиты и др.








