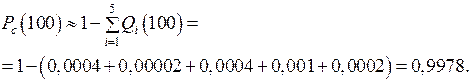Средней наработкой на отказ называется отношение суммарной наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки.
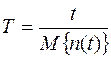 ,
,  (1.25)
(1.25)
где t – суммарная наработка; n(t) – число отказов, наступивших в течение этой наработки; М{n(t)} – математическое ожидание этого числа.
Статистически средняя наработка на отказ вычисляется по формуле
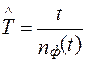 , (1.26)
, (1.26)
где n ф(t) – число фактических отказов в течение наработки t.
Наработка на отказ является достаточно наглядной характеристикой надежности, поэтому она получила широкое распространение на практике.
Параметр потока отказов и наработка на отказ характеризуют надежность ремонтируемого изделия и не учитывают времени, потребного на его восстановление. Следовательно, они не характеризуют готовности изделия к выполнению своих функций в нужное время. Для этой цели вводятся такие критерии, как коэффициент готовности и коэффициент вынужденного простоя.
Коэффициентом готовности называется вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается.
Согласно данному определению,
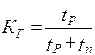 , (1.27)
, (1.27)
где t р – суммарное время работоспособного состояния объекта; t п – суммарное время, в течение которого объект не использовался по назначению. Значения времени tp и t п вычисляются по формулам:
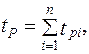
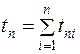 , (1.28)
, (1.28)
где t Р i – время работы изделия между (i – 1)-м и i-м отказом; t п – время вынужденного простоя после i-го отказа; п – число отказов (ремонтов) изделия.
Выражение (1.27) является статистическим определением коэффициента готовности. Для перехода к вероятностной трактовке величины t р и tn заменяются математическими ожиданиями времени между соседними отказами и времени восстановления соответственно. Тогда

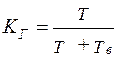 , (1.29)
, (1.29)
где Т – наработка на отказ; Тв – среднее время восстановления.
Коэффициентом вынужденного простоя называется отношение времени вынужденного простоя к сумме времени исправной работы и времени вынужденных простоев изделия, взятых за один и тот же календарный срок. Согласно определению,
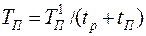 (1.30)
(1.30)
или, переходя к средним величинам,
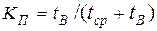 . (1.31)
. (1.31)
Коэффициент готовности и коэффициент вынужденного простоя связаны между собой зависимостью
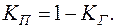 (1.32)
(1.32)
При анализе надежности восстанавливаемых систем обычно коэффициент готовности вычисляют по формуле
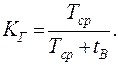 (1.33)
(1.33)
Формула (1.31) верна только в том случае, если поток отказов простейший, и тогда tcp = T.
Часто коэффициент готовности отождествляют с вероятностью того, что в любой момент времени восстанавливаемая система исправна. На самом деле указанные характеристики неравноценны и могут быть отождествлены при определенных допущениях.
Действительно, вероятность возникновения отказа ремонтируемой системы в начале эксплуатации мала. С ростом времени t эта вероятность возрастает. Это означает, что вероятность застать систему в исправном состоянии в начале эксплуатации будет выше, чем по истечении некоторого времени. Между тем коэффициент готовности не зависит от времени работы.
Для выяснения физического смысла коэффициента готовности КГ необходимо воспользоваться формулой для вероятности застать систему в исправном состоянии. При этом рассматривается наиболее простой случай, когда интенсивность отказов и интенсивность восстановления есть величины постоянные.
Предполагая, что при t = 0 система находится в исправном состоянии (Р(0) = 1), вероятность застать систему в исправном состоянии можно определить из выражений:
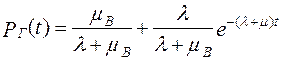 ,
,
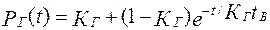 , (1.34)
, (1.34)
где t – средняя наработка на отказ;
t В – время восстановления;
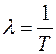 ,
, 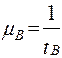 ,
, 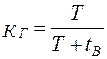 . (1.35)
. (1.35)
Последнее выражение устанавливает зависимость между коэффициентом готовности системы и вероятностью застать ее в исправном состоянии в любой момент времени t.
Из (1.34) видно, что P Г(t) →КГ при t → ∞, т. е. практически коэффициент готовности имеет смысл вероятности застать объект в исправном состоянии при установившемся процессе эксплуатации.
В некоторых случаях критериями надежности восстанавливаемых систем могут быть также показатели безотказности невосстанавливаемых систем, например: вероятность безотказной работы, частота отказов, средняя наработка до отказа, интенсивность отказов. Такая необходимость возникает всегда, когда имеет смысл оценить надежность восстанавливаемой системы до первого отказа, а также в случае, когда применяется резервирование с восстановлением резервных устройств, отказавших в процессе работы системы, причем отказ всей резервированной системы не допускается.
1.5. Примеры решения задач
Предлагается несколько простых примеров решения задач. Следует помнить, что частота, интенсивность отказов и параметр потока отказов, вычисленные по формулам (1.35), (1.6) и (1.13), являются постоянными в диапазоне интервала времени ∆ t, а функции 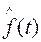 ,
, 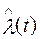 ,
, 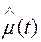 – ступенчатыми кривыми или гистограммами. Для удобства изложения в дальнейшем при решении задач на определение частоты, интенсивности и параметра потока отказов по статистическим данным об отказах изделий ответы относятся к середине интервала ∆ t. При этом результаты вычислений графически представляются не в виде гистограмм, а в виде точек, отнесенных к середине интервалов ∆ ti и соединенных плавной кривой.
– ступенчатыми кривыми или гистограммами. Для удобства изложения в дальнейшем при решении задач на определение частоты, интенсивности и параметра потока отказов по статистическим данным об отказах изделий ответы относятся к середине интервала ∆ t. При этом результаты вычислений графически представляются не в виде гистограмм, а в виде точек, отнесенных к середине интервалов ∆ ti и соединенных плавной кривой.
Пример 1
Допустим, что на испытание поставлено 1000 однотипных электронных ламп. За 3000 ч отказало 80 ламп, требуется определить вероятность безотказной работы P(t) и вероятность отказа Q(t) в течение 3000 ч
| Дано: N = 1000 шт. ∆ t = 3000 ч n = 80 шт. | Решение:
| |
| Найти: P ( t ) Q ( t ) | ||
Пример 2
Допустим, что на испытание поставлено 1000 однотипных электронных ламп. За первые 3000 ч отказало 80 ламп, а за интервал времени 3000–4000 ч отказало еще 50 ламп. Требуется определить частоту f(∆ t) и интенсивность λ(∆ t) отказов электронных ламп в промежутке времени ∆ t = 3000–4000 ч.
| Дано: N = 1000 шт. ∆ t1 = 3000 ч n1 = 80 шт. ∆ t2 = [3000, 4000] n2 = 50 шт. | Решение:
где
| |
| Найти: a(∆ t2) λ(∆ t2) | ||
Пример 3
На испытание поставлено N0 = 400 изделий. За время t = 3000 ч отказало n(t) = 200 изделий, за интервал ∆ t = 100 ч отказало n(∆ t) = 100 изделий. Требуется определить вероятность безотказной работы за 3000 ч, вероятность безотказной работы за 3100 ч, вероятность безотказной работы за 3050 ч, частоту отказов f(3050), интенсивность отказов λ(3050).
|
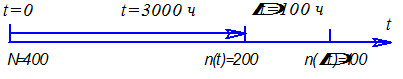
Рис. 1.3. Временной график
| Дано: N = 400 шт. t = 3000 ч n = 200 шт. ∆ t = 100 ч n (∆ t ) = 100 шт. | Решение: Вероятность безотказной работы определяется по формуле
Для t = 3000 ч (начало интервала)
Для t = 3100 ч (конец интервала)
Среднее время исправно работающих изделий в интервале ∆ t: Число изделий, отказавших за время t = 3050 ч:
| |
| Найти: Р(3000) Р(3100) Р(3050) f(3050) f(3000) f(3100) λ(3000) λ(3050) λ(3100) | ||
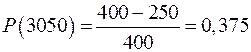 .
.
Определяется частота отказа:
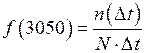 ;
; 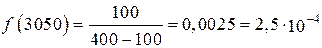 ч–1.
ч–1.
Так же определяется частота отказов за интервалы 3000 и 3100 ч, причем началом интервалов является t = 0.
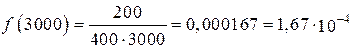 ч–1;
ч–1;
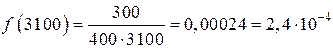 ч–1.
ч–1.
Определяется интенсивность отказов:
а) в интервале ∆ t = 3050 ч, 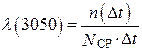 ;
;
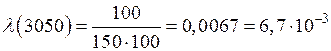 ч–1;
ч–1;
б) в интервале 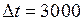 ч,
ч, 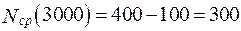 шт.;
шт.;
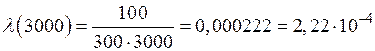 ч–1;
ч–1;
в) в интервале 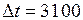 ч,
ч, 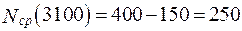 шт.;
шт.;
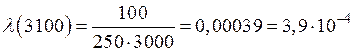 ч–1.
ч–1.
Пример 4
В течение некоторого периода времени производилось наблюдение за работой одного объекта. За весь период зарегистрировано n = 15 отказов. До начала наблюдений объект проработал 258 ч, к концу наблюдения наработка составила 1233 ч. Определить среднюю наработку на отказ tср.
| Дано: n = 15 t1 = 258 ч t2 = 1233 ч | Решение: Наработка за указанный период составила ∆ t = t1 – t2 = 1233 – 258 = 975 ч. Наработка на отказ по статистическим данным определяется по формуле
| |
| Найти: tср | ||
где ti – время исправной работы между (i – 1) и i отказами; n – число отказов за некоторое время t.
Приняв 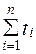 = 975 ч, можно определить среднюю наработку на отказ
= 975 ч, можно определить среднюю наработку на отказ
tср = 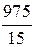 = 65 ч.
= 65 ч.
Пример 5
Производилось наблюдение за работой трех однотипных объектов. За период наблюдения было зафиксировано по первому объекту 6 отказов, по второму – 11 отказов, третьему – 8 отказов. Наработка первого объекта t1 = 6181 ч, второго t2 = 329 ч, третьего t3 = 245 ч. Определить наработку объектов на отказ.
| Дано: N = 3 шт. n1 = 6 шт. n2 = 11 шт. n3 = 8 шт. t1 = 181 ч t2 = 329 ч t3 = 245 ч | Решение: 1-й вариант решения:
|
| Найти: t ср | |
| 2-й вариант решения: | |
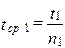 ,
, 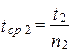 ,
, 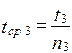 ;
;
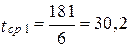 ч;
ч; 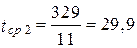 ч;
ч; 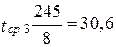 ч;
ч;
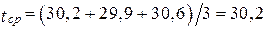 ч.
ч.
Как видно, у задачи есть два варианта решения. Первый основан на использовании общей формулы вычисления средней наработки; второй – более детальный: сначала находится средняя наработка для каждого элемента, а среднее значение этих чисел и есть то, что определяется.
Пример 6
Система состоит из 5 приборов, причем отказ любого одного из них ведет к отказу системы. Известно, что первый отказал 34 раза в течение 952 ч работы, второй – 24 раза в течение 960 ч работы, а остальные приборы в течение 210 ч работы отказали 4, 6 и 5 раз соответственно. Требуется определить наработку на отказ системы в целом, если справедлив экспоненциальный закон надежности для каждого из пяти приборов.
| Дано: N = 5 шт. n1 = 34 шт. n2 = 24 шт. n3 = 4 шт. n4 = 6 шт. n5 = 5 шт. t1 = 952 ч t2 = 960 ч t3–5 = 210 ч
| Решение: Используются следующие соотношения:
Определяется интенсивность отказов для каждого прибора (N = 1):
где Nср – среднее число исправно работающих изделий в интервале ∆t.
| |
| Найти: tср | ||
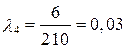 ч –1;
ч –1; 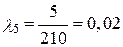 ч–1;
ч–1;
или
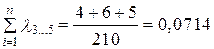 ч–1;
ч–1;
тогда интенсивность отказов системы будет
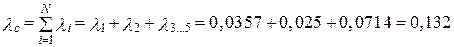 ч–1.
ч–1.
Средняя наработка на отказ системы равна
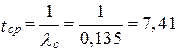 ч.
ч.
Пример 7
За наблюдаемый период эксплуатации в аппаратуре было зафиксировано 8 отказов. Время восстановления составило: t1 = 12 мин, t2 = 23 мин, t3 = 15 мин, t4 = 9 мин, t5 = 17 мин, t6 = 28 мин, t7 = 25 мин, t8 = 31 мин.
Требуется определить среднее время восстановления аппаратуры.
| Дано: n = 8 отказов t1 = 12 мин t2 = 23 мин t3 = 15 мин t4 = 9 мин t5 = 17 мин t6 = 28 мин t7 = 25 мин t8 = 31 мин | Решение:
|
| Найти: tср.в |
Пример 8
Аппаратура имела среднюю наработку на отказ tcp = 65 ч и среднее время восстановления t в = 1,25 ч. Требуется определить коэффициент готовности Кг.
| Дано: tcp = 65 ч t в = 1,25 ч | Решение:
|
| Найти: Кг |
Пример 9
Пусть время работы элемента до отказа подчинено экспоненциальному закону λ = 2,5 · 10–5 ч–1. Требуется определить вероятность безотказной работы P(t), частоту отказов f(t) и среднюю наработку на отказ t ср, если t = 500, 1000, 2000 ч.
| Дано: λ = 2,5·10–5 ч–1 t1 = 500 ч t2 = 1000 ч t3 = 2000 ч | Решение:
|
| Найти: P(t) f(t) t ср |
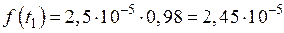 ч–1;
ч–1;
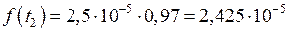 ч–1;
ч–1;
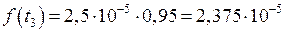 ч–1;
ч–1;
tср = 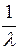 ;
;
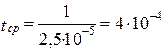 ч.
ч.
Пример 10
Время работы изделия до отказа подчиняется закону распределения Рэлея. Требуется определить количественные характеристики: P(t), f(t), λ(t), t ср при t1 = 500 ч, t2 = 1000 ч, t3 = 2000 ч, если параметр распределения σ = 1000 ч.
| Дано: t1 = 500 ч t2 = 1000 ч t3 = 2000 ч σ = 1000 ч | Решение: Необходимо воспользоваться формулами, соответствующими закону распределения Рэлея ([8], табл. 1.1)
|
| Найти: P(t) f(t) λ(t) t ср |
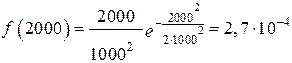 ч–1;
ч–1;
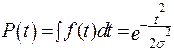 ;
;
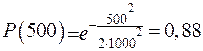 ;
;
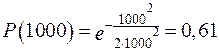 ;
;
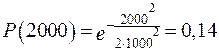 ;
;
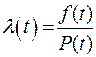 ;
;
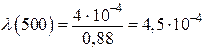 ч–1;
ч–1;
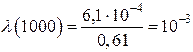 ч–1;
ч–1;
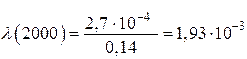 ч–1;
ч–1;
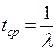 ;
;
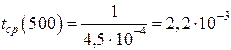 ч;
ч;
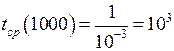 ч;
ч;
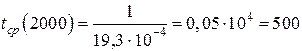 ч.
ч.
Пример 11
Время безотказной работы гироскопического устройства с шарикоподшипниками в осях ротора гироскопа подчиняется закону Вейбулла – Гнеденко с параметрами k = 1,5, λо = 10–4 ч–1, а время его работы t = 100 ч. Требуется вычислить количественные характеристики надежности такого устройства.
| Дано: k = 1,5 λо = 10–4 ч–1 t = 100 ч | Решение: Используются формулы закона Вейбулла – Гнеденко для определения количественных характеристик. Определяется вероятность безотказной работы:
Частота отказов определяется по формуле
|
| Найти: P(t) f(t) λ(t) tср |
Тогда
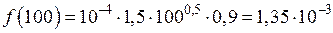 ч–1
ч–1
Интенсивность отказов определяется по формуле
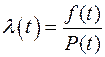 ;
;
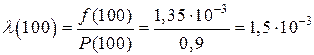 ч–1.
ч–1.
Вычисляется средняя наработка до первого отказа
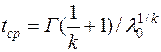 .
.
Сначала вычисляют значение гамма-функции, воспользовавшись справочными данными ([8], табл. П.7.18):
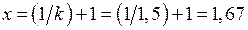 .
.
Значения гамма-функции
| х | Г (х) |
| 1,67 | 0,90330 |
Полученные значения подставляют в формулу [8, с. 38]:
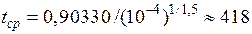 ч.
ч.
Пример 12
Известно, что интенсивность отказов λ = 0,02 ч–1, а среднее время восстановления tВ = 10 ч. Требуется вычислить коэффициент готовности и функцию готовности изделия.
| Дано: t В = 10 ч λ = 0,02 ч–1 | Решение: Коэффициент готовности изделия определяется по формуле
Средняя наработка до первого отказа равна Тогда |
| Найти: КГ РГ |
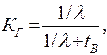
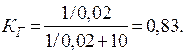
Функция готовности изделия определяется по формуле
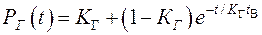 ,
,
где t – любой момент времени, при t = 0 система находится в исправном состоянии.
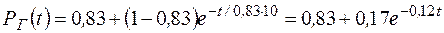 .
.
Пример 13
Система состоит из 12 600 элементов, средняя интенсивность отказов которых λср = 0,32·10–6 ч–1.
Необходимо определить вероятность безотказной работы в течение t = 50 ч.
| Дано: N = 12 600 λср= 0,32·10–6 ч–1 t = 50 ч | Решение: Интенсивность отказов системы определяется по формуле
Вероятность безотказной работы по экспоненциальному закону равна:
|
| Найти: P(t) |
Пример 14
Система состоит из N = 5 блоков. Надежность блоков характеризует- ся вероятностью безотказной работы в течение времени t, которая равна:
p1(t) = 0,98; p2(t) = 0,99; p3(t) = 0,97; p4(t) = 0,985; p5(t) = 0,975.
Требуется определить вероятность безотказной работы системы.
| Дано: N = 5 p1(t) = 0,98 p2(t) = 0,99 p3(t) = 0,97 p4(t) = 0,985 p5(t) = 0,975 | Решение: Необходимо воспользоваться формулой для определения безотказной работы системы:
Вероятности p1(t), p2(t), p3(t), p4(t), p5(t) близки к единице, поэтому вычислить Рс(t) удобно, пользуясь приближенной формулой. В данном случае q1 = 0,02; q2 = 0,01; q3 = 0,03; q4 = 0,015; |
| Найти: Рс(t) |
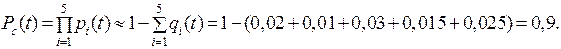
Пример 15
Система состоит из трех устройств. Интенсивность отказов электронного устройства равна λ1 = 0,16·10–3 ч–1 = const. Интенсивности отказов двух электромеханических устройств линейно зависят от времени и определяются следующими формулами: λ2 = 0,23·10 –4t ч–1, λ3 = 0,06·10–6t2,6 ч–1.
Нужно рассчитать вероятность безотказной работы изделия в течение 100 ч.
| Дано: N = 3 λ1 = 0,16 ·10–3 ч–1 λ2 = 0,23 ·10–4t ч–1 λ3 = 0,06 ·10–6t2,6 ч –1 t = 100 ч | Решение: Так как λ ≠ const, то на основании формулы можно написать
|
| Найти: Р(t) | |
при t = 100 ч
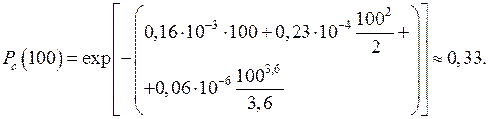
Пример 16
Система состоит из трех блоков, средняя наработка до первого отказа которых равна Т1 =160 ч, Т2 = 320 ч, Т3 = 600 ч. Для блоков справедлив экспоненциальный закон надежности.
Требуется определить среднюю наработку до первого отказа системы.
| Дано: N = 3 Т1 = 160 ч Т2 = 320 ч Т3 = 600 ч | Решение: Согласно экспоненциальному закону Интенсивность отказов системы:
Средняя наработка до первого отказа системы:
|
| Найти: tср.с | |
следовательно,
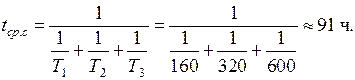
Пример 17
Система состоит из двух устройств. Вероятности безотказной работы каждого из них в течение времени t = 100 ч равны: р1(100) = 0,95; р2 (100) = 0,97. Справедлив экспоненциальный закон надежности. Необходимо найти среднюю наработку до первого отказа системы tср.с.
| Дано: N = 2 t = 100 ч р1 (100) = 0,95 р2 (100) = 0,97 | Решение: Определяется вероятность безотказной работы изделия:
Определяется интенсивность отказов изделия по формуле
|
| Найти: tcp.c |
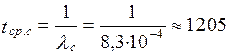 ч.
ч.
| |
Пример 18
Вероятность безотказной работы одного элемента в течение времени t равна p(t) = 0,9997. Требуется определить вероятность безотказной работы системы, состоящей из N = 100 таких же элементов.
| Дано: p(t) = 0,9997 N = 100 | Решение: 1-й вариант решения: Если у всех элементов системы одинаковая надежность, то
2-й вариант решения: |
| Найти: Pc |
Так как вероятность  близка к единице, то можно воспользоваться следующей формулой:
близка к единице, то можно воспользоваться следующей формулой:
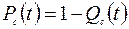 .
.
Для одного элемента системы:
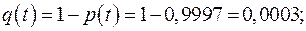 т. е.
т. е.
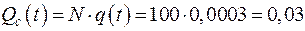 .
.
Из 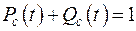 следует
следует 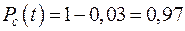 .
.
Получается, что первый вариант решения более точен.
Пример 19
Вероятность безотказной работы системы в течение времени t равна
Рс(t) = 0,95. Система состоит из N = 120 равнонадежных элементов. Требуется определить вероятность безотказной работы элемента р i(t).
| Дано: Рс(t) = 0,95 N = 120 | Решение: Очевидно, что вероятность безотказной работы элемента будет
|
| Найти: Р i(t) |
Тогда
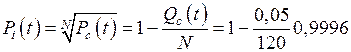 .
.
Пример 20
В системе N с = 2500 элементов, вероятность безотказной работы ее в течение одного часа Рс(1) = 98 %. Предполагается, что все элементы равнонадежны и интенсивность отказов элементов λ = 8,4·10–6 ч–1. Требуется определить среднюю наработку до первого отказа системы t ср.с.
| Дано: N с = 2500 Рс(1) = 98 % λ = 8,4·10–6 ч–1 | Решение: Интенсивность отказов системы определим по формуле λс = N · λ = 8,4 · 10 –6 · 2500 = 0,021 ч–1, средняя наработка до первого отказа системы равна: t ср.с = 1/λс= 1/0,021 = 47,6 ч.
|
| Найти: t ср.с |
Пример 21
Система состоит из пяти приборов, вероятности исправной работы которых в течение времени t = 100 ч равны: p1(100) = 0,9996; p2(100) = 0,9998; p3(100) = 0,9996; p4(100) = 0,999; p5(100) = 0,9998. Требуется определить частоту отказов системы в момент времени t = 100 ч.
Предполагается, что отказы приборов независимы и для них справедлив экспоненциальный закон надежности.
| Дано: t = 100 ч p1(100) = 0,9996 p2(100) = 0,9998 p3(100) = 0,9996 p4(100) = 0,999 p5(100) = 0,9998 | Решение: По условиям задачи отказы приборов независимы, поэтому вероятность безотказной работы системы равна произведению вероятностей безотказной работы приборов. Тогда для случая высоконадежных систем (при значенях р i, близких к единице) имеем:
|
| Найти: fс | |
Так как вероятность безотказной работы системы близка к единице, то в соответствии с формулой
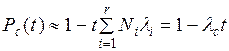
интенсивность отказов можно вычислить следующим образом:
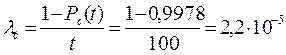 ч–1,
ч–1,
тогда частоту отказов определим в соответствии с формулой:
ас(t) 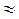 λс(1 – λс t) = 2,2·10–5(1 – 2,2·10–5·100) = 2,195·10–5 ч–1.
λс(1 – λс t) = 2,2·10–5(1 – 2,2·10–5·100) = 2,195·10–5 ч–1.
Пример 22
Изделие состоит из 12 маломощных низкочастотных германиевых транзисторов, 4 плоскостных кремниевых выпрямителей, 50 керамических конденсаторов, 168 резисторов типа МЛТ, 1 силового трансформатора, 2 накальных трансформаторов, 5 дросселей и 4 катушек индуктивности. Необходимо найти вероятность безотказной работы изделия в течение t = 200 ч и среднюю наработку до первого отказа.
| Дано: N1 = 12 N2 = 4 N3 = 50 N4 = 168 N5 = 1 N6 = 2 N7 = 5 N8 = 4 t = 200 ч | Решение: Для решения данной задачи вычисляются величины интенсивности отказов изделия, затем составляется и заполняется таблица 1.2. Значения интенсивности отказов элементов выбираются из [8] (табл. П.3.1, П.3.5, П.3.7).
|
| Найти: Рс(200) tср.с |
Таблица 1.2
| Наименование и тип элемента | Количество элементов Ni | Интенсивность отказов, ч–1 | |
| λi · 10 –5 | Ni λi · 10 –5 | ||
| Транзистор маломощный низкочастотный германиевый | 12 | 0,3 | 3,6 |
| Выпрямитель плоскостной кремниевый | 4 | 0,5 | 2 |
| Конденсатор керамический | 50 | 0,14 | 7 |
| Резистор типа МЛТ | 168 | 0,05 | 8,4 |
| Трансформатор силовой | 1 | 0,3 | 0,3 |
| Трансформатор накальный | 2 | 0,2 | 0,4 |
| Дроссель | 5 | 0,1 | 0,5 |
| Катушка индуктивности | 4 | 0,05 | 0,2 |
Интенсивность отказов элементов
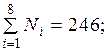
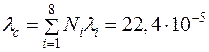 ч–1.
ч–1.
По данным табл. 1.2 и по формуле для экспоненциального закона находится вероятность безотказной работы изделия в течение t = 200 ч и средняя наработка до первого отказа:
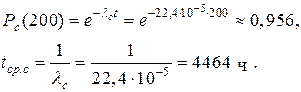









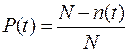 ;
;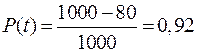 ;
;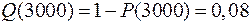 или
или 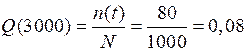 .
.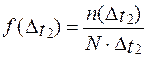 ;
;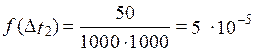 ч–1;
ч–1;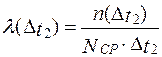 ,
,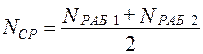 ;
;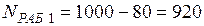 шт.;
шт.;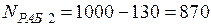 шт.;
шт.;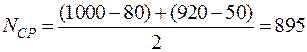 шт.;
шт.;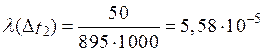 ч–1.
ч–1.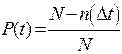 .
.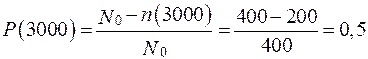 .
.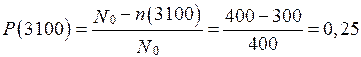 .
.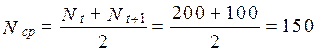 .
.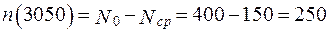 , тогда
, тогда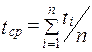 ,
,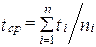 ;
;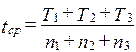 ;
;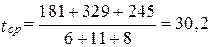 ч;
ч;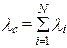 ;
; 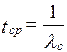 .
.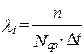 ,
,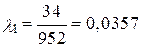 ч–1;
ч–1; 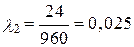 ч–1;
ч–1;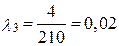 ч–1;
ч–1;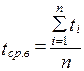 ;
;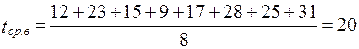 мин.
мин.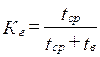 ;
;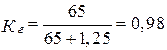 .
.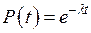 ;
;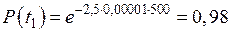 ;
;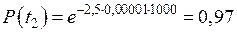 ;
;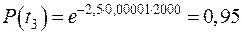 ;
;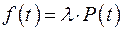 ;
;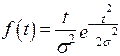 ;
;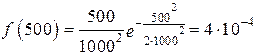 ч–1;
ч–1;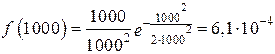 ч–1;
ч–1;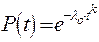 ;
;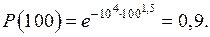
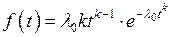 .
.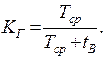
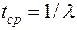 .
.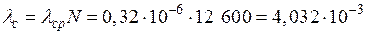 ч–1.
ч–1.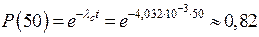 .
.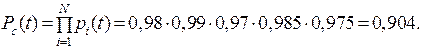
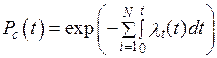
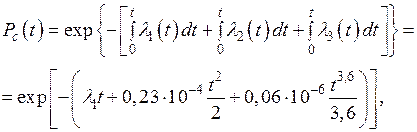
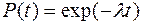 .
.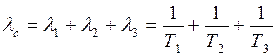 .
.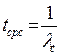 ,
,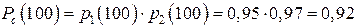 .
.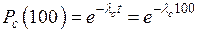 ;
;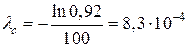 ч–1,
ч–1,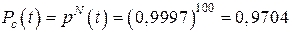 .
.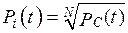 . Так как
. Так как 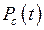 близка к единице, то вычисления удобно выполнять по формуле
близка к единице, то вычисления удобно выполнять по формуле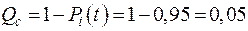 .
.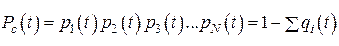 ,
,