Средней наработкой до первого отказа называется математическое ожидание времени работы объекта до отказа.

Дата: 2025-05-01; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Математическое ожидание средней наработки до отказа T ₁ вычисляется через частоту отказов (плотность распределения времени безотказной
работы):

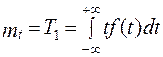. (1.12)

Зная, что t > 0 и P(0) = 1, а P(∞) = 0, определяют T₁:

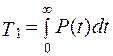. (1.13)

Средняя наработка до первого отказа, согласно статистическим данным об отказах, вычисляется по формуле

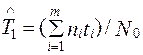, (1.14)

где t _i – время безотказной работы i-го образца; N₀ – число испытываемых объектов.

Для определения средней наработки до первого отказа необходимо знать моменты выхода из строя всех испытываемых объектов. Поэтому для вычисления 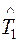пользоваться данной формулой неудобно. Имея данные о количестве вышедших из строя элементов n_i в каждом i-м интервале времени, среднюю наработку до первого отказа лучше определять по уравнению

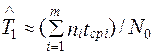, (1.15)

где t _ср и m находятся по следующим формулам:

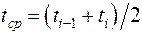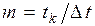, , (1.16)

где t_i–1 – время начала i-го интервала; t_i – время конца i-го интервала; t_k – время, в течение которого вышли из строя все элементы; 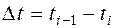– интервал времени.

При расчетах надежности технических устройств часто применяются законы распределения: экспоненциальный, усеченный нормальный, Рэлея, гамма, Вейбулла – Гнеденко, логарифмически-нормальный. В табл. 1.1 приведены выражения для расчета количественных характеристик объектов, соответствующих перечисленным законам распределения времени их безотказной работы.

Таблица 1.1

Интенсивность отказов элементов

Закон распределения	Частота отказов (плотность распределения)	Вероятность безотказной работы	Интенсивность отказов	Средняя наработка до первого отказа
Экспоненциальный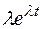
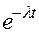
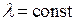
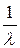
Рэлея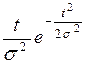
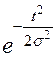
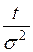
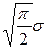
Гамма (при k целом)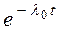
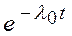
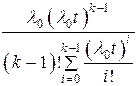
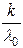
Вейбулла – Гнеденко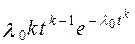
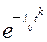
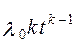
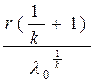
Усеченный нормальный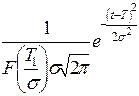
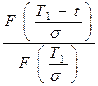
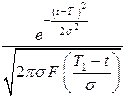
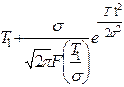
Логарифми- чески- нормальный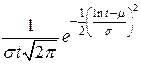

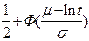
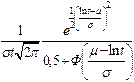
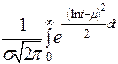
Из приведенных соотношений видно, что все характеристики, кроме средней наработки до первого отказа, зависят от времени (являются функциями времени). На рис. 1.2 показаны зависимости количественных характеристик надежности объектов от времени.

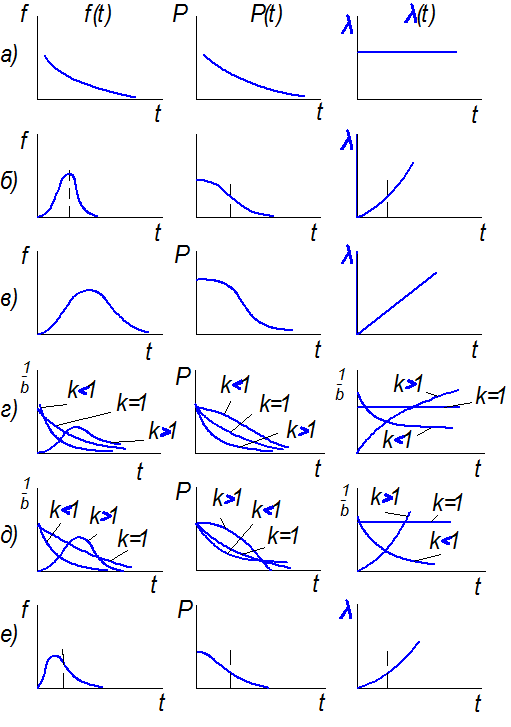
Рис. 1.2. Зависимости количественных характеристик на­дежности от времени:

а – экспоненциальный закон; б – усеченный нормальный закон; в – закон Рэлея;
г – гамма-распределение: д – закон Вейбулла – Гнеденко;
е – логарифмически-нормальный закон

Рассмотренные критерии надежности позволяют достаточно полно оценивать надежность невосстанавливаемых объектов, а также надежность восстанавливаемых объектов до первого отказа. Наличие нескольких критериев не означает, что всегда нужно оценивать надежность объектов по всем характеристикам.

Наиболее полной характеристикой надежности является частота отказов f(t) (плотность распределения), она содержит в себе все данные о случайном явлении – времени безотказной работы.

Средняя наработка до первого отказа является достаточно наглядной характеристикой надежности. Однако применение этого критерия для оценки надежности сложной системы ограничено в тех случаях, когда:

– время работы системы гораздо меньше среднего времени безотказной работы;

– закон распределения времени безотказной работы не однопараметрический и для достижения полной оценки требуются моменты высших порядков;

– система резервированная;

– интенсивность отказов не постоянная;

– время работы отдельных частей сложной системы разное.

Интенсивность отказа – наиболее удобная характеристика надежности простейших элементов, так как позволяет просто вычислять количественные характеристики надежности сложных систем.

Наиболее целесообразно оценивать надежность сложных систем по критерию вероятности безотказной работы, так как:

– она входит в качестве сомножителя в другие, более общие характеристики систем, например в эффективность и стоимость (цена и стоимость различаются);

– характеризует надежность с учетом изменения во времени;

– может быть получена сравнительно простыми расчетами в процессе про­ек­тирования систем и оценена в процессе испытаний.

1.4. Критерии надежности восстанавливаемых изделий

Пусть на испытании находится N изделий, и пусть от­казавшие изделия немедленно заменяются исправными (новыми или отремонтированными).
Испытания счита­ются законченными, если число отказов достигает величины, достаточной для оценки надежности с определенной доверительной вероятностью. Если не учитывать времени, потребного на восстановление системы, то ко­личественными характеристиками надежности могут быть параметр потока отказов μ(t) и наработка на от­каз Т.

Параметром потока отказов называется отношение числа отказавших изделий в единицу времени к числу испытываемых изделий при условии, что все вышедшие из строя изделия заменяются исправными (новыми или отремонтированными).

Согласно определению,

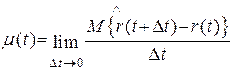, (1.17)

где ∆ t – малый отрезок наработки; r(t) – число отказов, наступивших от начального момента времени до достижения наработки t. Разность r(t +∆ t) – r(t) представляет собой число отказов на отрезке ∆ t.

Статистическую оценку параметра потока отказов дают по формуле

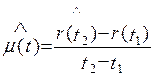. (1.18)

Для стационарных потоков можно применять формулу

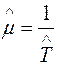, (1.19)

где 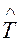– оценка средней наработки на отказ;

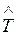
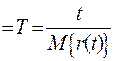, здесь t – суммарная наработка, r(t) – число отказов, наступивших в течение этой наработки, 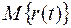– математическое ожидание этого числа.

Параметр потока отказов определяется также по формуле

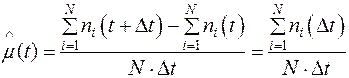, (1.20)

где 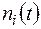– число отказавших образцов в интервале вре­мени от 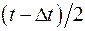до 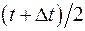; N – число испытываемых об­разцов; 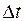– интервал времени.

Формула (1.18) является статистическим определе­нием параметра потока отказов.

Параметр потока отказов и частота отказов для орди­нарных потоков с ограниченным последействием связаны интегральным уравнением Вольтерра второго рода

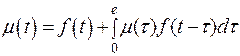. (1.21)

По известной f(t) можно найти все количественные характеристики надежности невосстанавливаемых изде­лий. Поэтому (1.21) является основным уравнением, свя­зывающим количественные характеристики надежности невосстанавливаемых и восстанавливаемых изделий при мгновенном восстановлении.

Уравнение (1.21) можно записать в операторной форме:

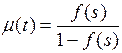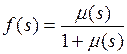, . (1.22)

Соотношения (1.22) позволяют найти одну характе­ристику через другую, если существуют преобразования Лапласа функций a(s) и m(s) и обратные преобразова­ния выражений (1.22).

Параметр потока отказов обладает следующими важ­ными свойствами:

1) для любого момента времени независимо от зако­на распределения времени безотказной работы параметр потока отказов больше, чем частота отказов, т. е. μ(t) >> f(t);

2) независимо от вида функции f(t) параметр пото­ка отказов μ( t) при
t → ∞ стремится к 1/Т_ср. Это важ­ное свойство параметра потока отказов означает, что при длительной эксплуатации ремонтируемого изделия поток его отказов независимо от закона распределения вре­мени безотказной работы становится стационарным. Од­нако это не означает, что интенсивность отказов есть величина постоянная;

3) если l(t) – возрастающая функция времени, то

l ( t) > μ(t) > f(t),

4) если l(t) – убывающая функция, то

f(t) > l(t) > μ(t);

5) при l(t) = const параметр потока отказов системы не равен сумме параметров потоков отказов элементов, т. е.

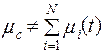. (1.23)

Согласно этому свойству параметра потока отказов можно утверждать, что при вычислении количественных харак­теристик надежности сложной системы нельзя суммиро­вать имеющиеся в настоящее время значения интенсивностей отказов элементов, полученные по статистиче­ским данным об отказах изделий в условиях эксплуата­ции, так как указанные величины являются фактически параметрами потока отказов;

6) при l(t) = l = const параметр потока отказов равен интенсивности отказов μ(t) = l(t) = l .

Сравнение свойств интенсивности и параметра потока отказов свидетельствует, что эти характеристики различны.

В настоящее время широко используются статистиче­ские данные об отказах, полученные в условиях эксплуа­тации аппаратуры. При этом они часто обрабатываются таким образом, что приводимые характеристики надеж­ности являются не интенсивностью отказов, а парамет­ром потока отказов μ(t). Это приводит к ошибкам при расче­тах надежности. В ряде случаев они могут быть значи­тельными.

Для получения интенсивности отказов элементов из статистических данных об отказах ремонтируемых систем необходимо воспользоваться формулой (1.6), для чего следует знать предысторию каждого элемента прин­ципиальной схемы. Это может существенно усложнить методику сбора статистических данных об отказах. По­этому целесообразно определять l(t) по параметру по­тока отказов μ(t). Методика расчета сводится к следую­щим вычислительным операциям:

– по статистическим данным об отказах элементов ремонтируемых изделий и по формуле (1.13) вычисляет­ся параметр потока отказов и строится гистограмма μ_i(t);

– гистограмма заменяется кривой, которая аппрокси­мируется уравнением;

– находится преобразование Лапласа μ_i(s) функции μ_i(t);

– по известной μ_i(s) на основании (1.15) записы­вается преобразование Лапласа f_i(s) частоты отказов;

– по известной f_i(s) находится обратное преобразо­вание частоты отказов f_i(t);

– находится аналитическое выражение для интенсив­ности отказов по формуле

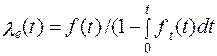; (1.24)

– строится график l _i(t).

Если имеется участок, где l _i(t) = l = const, то посто­янное значение интенсивности отказов принимается для оценки вероятности безотказной работы. При этом счи­тается справедливым экспоненциальный закон надежно­сти.

Приведенная методика не может быть применена, ес­ли не удается найти по f(s) обратное преобразование частоты отказов f(t). В этом случае приходится приме­нять приближенные методы решения интегрального урав­нения (1.21) или машинные методы расчета.