Вероятность безотказной работы по статистическим данным об отказах оценивается выражением

Дата: 2025-05-01; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

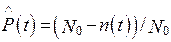, (1.2)

где 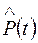– статистическая оценка вероятности безотказной работы; N₀ – число объектов в начале работы (серии испытаний); n(t) – число отказавших элементов за время t.

На практике, наряду с ВБР, определяют такую характеристику, как вероятность отказа Q(t).

Вероятностью отказа называется количественная мера того, что при определенных условиях эксплуатации в заданном интервале времени возникает хотя бы один отказ.

Отказ и безотказная работа являются событиями несовместными и противоположными, поэтому при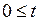

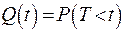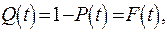, (1.3)

где 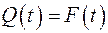– интегральная функция распределения случайной величины.

Статистически вероятность отказа равна [3]:

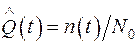, (1.4)

,

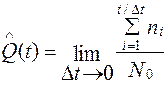где n_i – число неблагоприятных исходов; N₀ – общее число испытаний.

Если функция Q ( t ) дифференцируема, то производная от интегральной функции распределения – дифференциальный закон (плотность вероятности, плотность распределения) случайной величины Т – времени безотказной
работы:

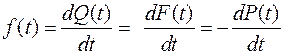. (1.5)

Частотой отказов по статистическим данным называется отношение числа отказавших элементов в единицу времени к первоначальному числу работающих (испытываемых) при условии, что все вышедшие из строя изделия не восстанавливаются. Согласно определению,

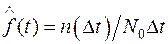или 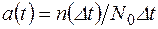, (1.6)

где 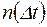– число отказавших элементов в интервале времени от 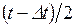до .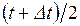

Частота отказов есть плотность вероятности (или закон распределения) времени работы изделия до первого отказа. Поэтому

,

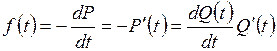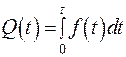, (1.7)

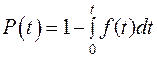. (1.8)

Интенсивностью отказов по статистическим данным называется отношение числа отказавших изделий в единицу времени к среднему числу изделий, исправно работающих в данный отрезок времени.

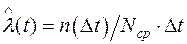, (1.9)

где N _ср = (N_i + N_{i +1})/2 – среднее число исправно работающих изделий в интервале 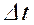; N_i – число изделий, исправно работающих в начале интервала 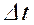; N_{i +1} – число изделий, исправно работающих в конце интервала .

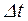Интенсивность отказов в вероятностной оценке есть условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ не возник.

Вероятностная оценка характеристики l (t) находится из выражения

l(t) = f(t) / P(t) (1.10)

или f(t) = l (t) P(t).

Интенсивность отказов и вероятность безотказной работы связаны между собой зависимостью

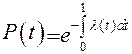. (1.11)