5 – обводная лупа; 6 – лупа для считывания делений планиметра
По счетному механизму берется четырехзначный отсчет. По шкале 1– тысячи, по шкале 2 – сотни и десятки, по шкале 3 единицы.

Рисунок 5.2 – Счетный механизм: 1, 2, 3 – шкалы планиметра;
4 – стрелка шкалы 1
В нашем примере стрелка 4 на счетном механизме находится между единицей и двойкой, поэтому отсчет начинается с одной тысячи. Нуль шкалы 3 располагается между семью и восьмью сотнями, следовательно, отсчет содержит семь сотен и шесть десятков, а на шкале 3 третий штрих совпадает со штрихом на шкале 2. Таким образом, отсчет по счетному механизму составляет 1763.
5.2 Принцип определения площади планиметром
Обводная лупа устанавливается в исходной точке А контура (точка выбирается произвольно) и по счетному механизму берется отсчет О1 , равный, например, 6437 (рисунок 5.3). Обводной шпиль ведется по контуру (по ходу часовой стрелки) и останавливается в исходной точке А, берется отсчет О2, допустим, равный 6556. Разность отсчетов
О2 – О1 = 0119 делений
дает площадь контура в делениях планиметра.
Если известна цена одного деления планиметра с, в м2/дел, т. е. число квадратных метров в одном делении планиметра, тогда площадь
S = c·(О2 – О1), м2.
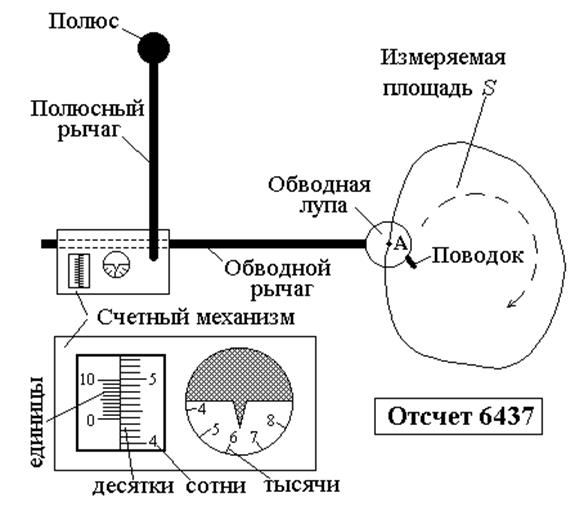
Рисунок 5.3 – Полярный планиметр
В нашем примере, если с = 3 м2/дел, то
S = 119дел·3 м2/дел = 357 м2.
5.3 Определение цены деления планиметра
Цена деления планиметра вычисляется путем тройного обвода известной площади SИ по формуле
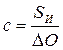 ,
,
где SИ – известная площадь квадрата, окружности или другой правильной фигуры;
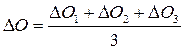 – средняя разность отсчетов по планиметру. Средняя разность DО вычисляется, если разности отсчетов
– средняя разность отсчетов по планиметру. Средняя разность DО вычисляется, если разности отсчетов
DО1 = О2 – О1, DО2 = О3 – О2 и DО3 = О4 – О3 отличаются не более чем на 2 единицы при площади до 200 делений, 3 единицы при площади 200 – 2000 делений и 4 единицы при площади свыше 2000 делений. В учебных целях допуски могут быть расширены.
Пример определения цены деления приводится в таблице 5.3.
Таблица 5.3 – Определение цены деления планиметра
| Отсчеты по планиметру | Разность отсчетов | Средняя разность отсчетов | Известная площадь S, м2 | Цена деления планиметра с, м2/дел. |
| О1 = 3455 | ||||
| DО1 = 111 | ||||
| О2 = 3566 | ||||
| DО2 = 113 | DО = 112 | 50000 | 446 | |
| О3 = 3679 | ||||
| DО3 = 112 | ||||
| О4 = 3791 |
5.4 Измерение площади
Контур площади обводится дважды планиметром и определяется площадь в таблице 5.4 по формуле
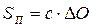 ,
,
где с – цена деления планиметра;
DО – средняя разность отсчетов по планиметру при двух обводах площади.
Таблица 5.4 – Определение площади планиметром
| Отсчеты по планиметру | Разность отсчетов | Средняя разность отсчетов, деления | Цена деления планиметра с, м2/дел. | Измеряемая площадь S, м2 |
| О1 = 2578 | ||||
| DО1 = 265 | ||||
| О2 = 2843 | DО = 266,5 | 446 | 118859 | |
| DО2 = 268 | ||||
| О3 = 3111 |
Результаты измерений показывают, что измеряемая площадь составляет
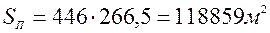
6 РЕШЕНИЕ ЗАДАЧ ПО ТОПОГРАФИЧЕСКОЙ КАРТЕ
6.1 Измерение по карте расстояний между точками
При определении расстояний пользуются нормальным поперечным масштабом, который представляет собой график (см. рисунок 6.1,а), позволяющий выполнять измерения с точностью 0,02 мм (отрезок а b на рис.6.1). Основание масштаба А = 2см, высота масштаба Н = 2,5см. Два см в масштабе 1:5000 это 100м в действительности на местности, а в масштабе 1:25000 - 500м. Так как основание масштаба разделено на 10 равных частей, то одной ее десятой (отрезок cd) соответствует расстояние в масштабе 1:5000 10 м, а в масштабе 1:25000 – 50м. Высота масштаба Н разделена на 10 равных частей, поэтому в отрезке а b содержится 1м при пользовании масштабом 1:5000 и 5м при масштабе 1:25000. Отрезок а b характеризует точность поперечного масштаба t, которая вычисляется по формуле
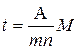 ,
,
где М – знаменатель численного масштаба.
Например, точность поперечного масштаба 1:25000 составит
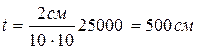 или t = 5м.
или t = 5м.
Для того, чтобы измерить расстояния между точками на карте необходимо иглами циркуля коснуться к точкам и полученный раствор циркуля приложить к поперечному масштабу таким образом, чтобы одна игла находилась на горизонтальной линии (точка e), а другая - на пересечении наклонной и горизонтальной линий масштаба (точка s). Измеряемый отрезок se состоит из трех частей so, or, и re. Этим частям соответствуют расстояние на местности в масштабе 1:5000 40 + 6 + 4 = 446 м, а в масштабе 1:25000 - 200 + 30 + 2000 = 2230 м.
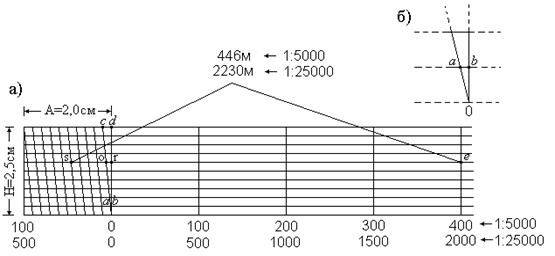
Рисунок 6.1 – Нормальный поперечный масштаб
Пример 1. Определить на карте масштаба 1:25000 (из комплекта учебных карт, который выдается преподавателем) расстояние между точкой в квадрате 6507 «Отметка 214,3» и точкой в квадрате 6508 «Отметка 197,1».
В результате измерения получен результат: 1480 м.
В таблице 6.1 приводятся варианты задач по определению расстояний между точками на карте масштаба 1:25000.
Таблица 6.1 – Отметки точек в квадратах по вариантам задач
| № варианта | Точка 1 | Точка 2 | ||
| Квадрат | Отметка | Квадрат | Отметка | |
| 1 | 6407 | 219,2 | 6409 | 211,0 |
| 2 | 6407 | 219,2 | 6507 | 214,3 |
| 3 | 6407 | 219,2 | 6508 | 197,1 |
| 4 | 6407 | 219,2 | 6409 | 201,6 |
| 5 | 6407 | 219,2 | 6606 | 205,0 |
| 6 | 6508 | 197,1 | 6507 | 214,3 |
| 7 | 6508 | 197,1 | 6606 | 205,0 |
| 8 | 6508 | 197,1 | 6608 | 186,1 |
| 9 | 6508 | 197,1 | 6509 | 171,3 |
| 10 | 6508 | 197,1 | 6409 | 201,6 |
| 11 | 6508 | 197,1 | 6409 | 211,0 |
| 12 | 6608 | 186,1 | 6507 | 214,3 |
| 13 | 6608 | 186,1 | 6606 | 205,0 |
| 14 | 6608 | 186,1 | 6607 | 178,4 |
| 15 | 6608 | 186,1 | 6709 | 127,7 |
| 16 | 6608 | 186,1 | 6709 | 121,8 |
| 17 | 6608 | 186,1 | 6707 | 183,1 |
| 18 | 6507 | 214,3 | 6607 | 178,4 |
| 19 | 6707 | 183,1 | 6607 | 178,4 |
| 20 | 6409 | 211,0 | 6409 | 201,6 |
| 21 | 6409 | 211,0 | 6410 | 171,5 |
| 22 | 6409 | 211,0 | 6510 | 153,0 |
| 23 | 6511 | 156,9 | 6510 | 167,0 |
| 24 | 6511 | 156,9 | 6610 | 131,2 |
| 25 | 6511 | 156,9 | 6611 | 156,8 |
6.2 Определение прямоугольных координат точек
Прямоугольными координатами точки являются абсцисса X и ордината Y. Абсцисса X - это расстояние от экватора до рассматриваемой точки, а ордината Y - расстояние от линии, отстоящей от осевого меридиана зоны на 500 км, до рассматриваемой точки. На рисунке 6.2 показаны координаты точки А: XA и YA.
Пример 2. Определить по карте масштаба 1:25000 прямоугольные координаты точки с отметкой 214.3, находящейся в квадрате 6507.
Западная и южная границы квадрата 6507 рассматриваются как оси x и y соответственно прямоугольной системы координат. Тогда x = 590 м и
y = 255 м.
Линия оси у находится от экватора (направление Y) на расстоянии 6065 км или 6065000м, следовательно, абсцисса точки с отметкой 214.3 составит
X = 6065000 + x = 6065000 + 590 = 6065590м.
Линия оси x расположена от осевого меридиана (направление Х) на расстоянии 4307км или 4307000м . Это означает, что ордината точки с отметкой 214.3 будет равна
Y = 4307000 + y = 4307000 + 255 = 4307255м.
Отделив шесть целых цифр, получим 307255 и цифру 4, которая указывает на номер шестиградусной зоны. 307255 – это расстояние от линии Х, отстоящей от осевого меридиана зоны на 500 км, до рассматриваемой точки.
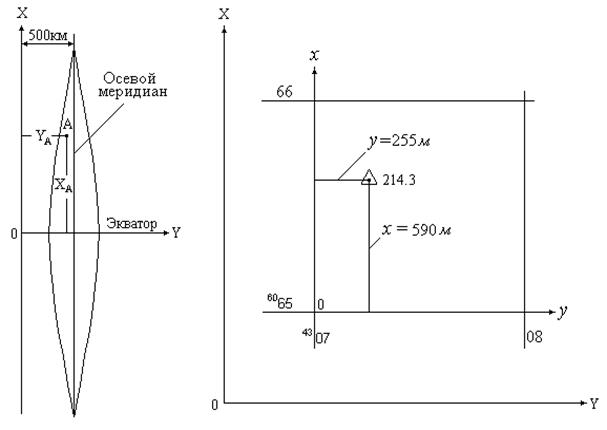 Рисунок 6.2 – Прямоугольные координаты точки
Рисунок 6.2 – Прямоугольные координаты точки
В таблице 6.2 приводятся варианты задач по определению координат точек на карте масштаба 1:25000.
Таблица 6.2 – Объекты в квадратах карты по вариантам задач
| № варианта | Квадрат | Наименование объекта |
| 1 | 6506 | Отметка 186,3 |
| 2 | 6407 | Отметка 219,2 |
| 3 | 6409 | Отметка 211,0 |
| 4 | 6409 | Отметка 201,6 |
| 5 | 6410 | Отметка 171,5 |
| 6 | 6411 | Отметка 159,7 |
| 7 | 6412 | Отметка 153,0 |
| 8 | 6412 | Отметка 155,7 |
| 9 | 6412 | Отметка 149,2 |
| 10 | 6508 | Отметка 197,1 |
| 11 | 6509 | Отметка 171,3 |
| 12 | 6510 | Отметка 153,0 |
| 13 | 6510 | Отметка 167,0 |
| 14 | 6511 | Отметка 156,9 |
| 15 | 6606 | Отметка 205,0 |
| 16 | 6607 | Отметка 178,4 |
| 17 | 6607 | Отметка 186,1 |
| 18 | 6610 | Отметка 171,8 |
| 19 | 6610 | Отметка 131,2 |
| 20 | 6611 | Отметка 156,8 |
| 21 | 6611 | Отметка 160,6 |
| 22 | 6612 | Отметка 156,2 |
| 23 | 6707 | Отметка 183,1 |
| 24 | 6709 | Отметка 121,8 |
| 25 | 6712 | Отметка 170,0 |
6.3 Определение географических координат точек
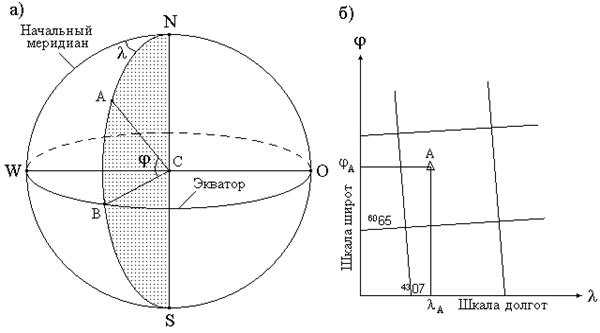
Географические координаты: j - широта точки, т.е. угол между отвесной линией, проходящей через точку, и плоскостью экватора; l - долгота точки - это двугранный угол между плоскостью меридиана, проходящего через рассматриваемую точку, и плоскостью начального меридиана.
На рисунке 6.3,а приводится иллюстрация географических координат.
Для определения географических координат необходимо из точки опустить перпендикуляры на шкалы широт и долгот и прочитать на этих шкалах широту и долготу точки (см. рисунок 6.3,а).