Практическое занятие 8. Оценка качества систем управления
Пример 1.
Определить значения не менее шести показателей качества замкнутой системы:
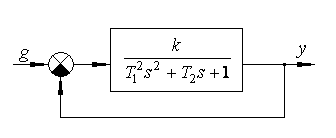
T1=0,5 c.; T2=1 c.; k=4; 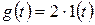 .
.
Найдем передаточные функции замкнутой системы:
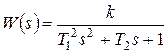 ,
,
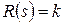 ,
, 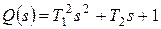 ,
,
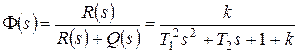 ,
,
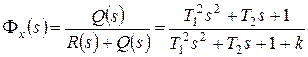 .
.
Характеристический полином системы 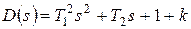 имеет второй порядок, все его коэффициенты положительны. Следовательно, система устойчива.
имеет второй порядок, все его коэффициенты положительны. Следовательно, система устойчива.
Рассчитаем установившуюся ошибку:
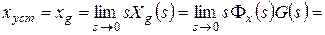
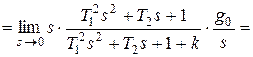
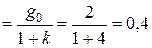 . (8.1)
. (8.1)
Найдем корни характеристического полинома:
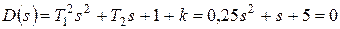 ,
,
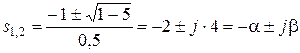 , a=2, b=4.
, a=2, b=4.
Найдем степень устойчивости h=2, (8.2)
колебательность 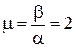 , (8.3)
, (8.3)
оценим время переходного процесса 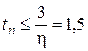 (8.4)
(8.4)
и рассчитаем затухание за период:
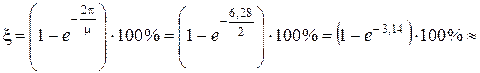
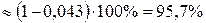 . (8.5)
. (8.5)
Для удобства определения запасов устойчивости по амплитуде и фазе рассмотрим логарифмические частотные характеристики разомкнутой системы.
Найдем корни знаменателя передаточной функции разомкнутой системы:
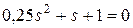 ,
,
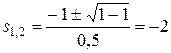 .
.
Корни вещественные кратные, следовательно, передаточная функция может быть представлена в виде
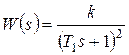 ,
,
тогда
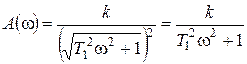 ,
,
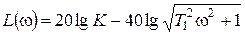 ,
,
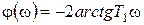 .
.
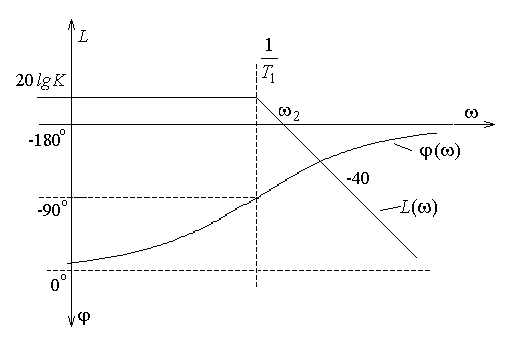
Для рассматриваемой системы: 
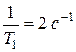 ,
, 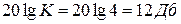 ; наклон идущего вниз участка
; наклон идущего вниз участка 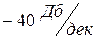 . Следовательно, расстояние в декадах от сопрягающей частоты
. Следовательно, расстояние в декадах от сопрягающей частоты 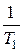 до частоты среза w2 составляет
до частоты среза w2 составляет 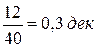 , что соответствует увеличению частоты в 2 раза (
, что соответствует увеличению частоты в 2 раза ( 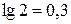 ). В результате w2=4 с-1, и запас по фазе может быть определен по формуле:
). В результате w2=4 с-1, и запас по фазе может быть определен по формуле:
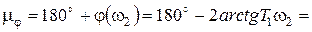
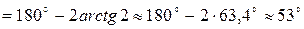 . (8.6)
. (8.6)
Для более точного расчета, который необходим, если расстояние между частотами будет меньше 0,3 дек., следует находить частоту среза из уравнения:
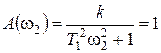 .
.
Дополнительно можно указать величину запаса устойчивости по амплитуде. Поскольку для рассматриваемой системы логарифмическая фазо-частотная характеристика асимптотически стремится к горизонтальной оси, не пересекая ее, запас по амплитуде равен бесконечности.
Пример 2.
Рассчитать установившуюся ошибку
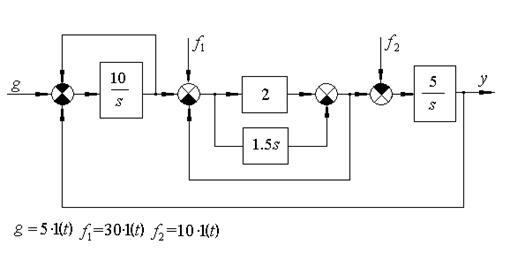
Упростим структурную схему с учетом известных соотношений для отрицательной обратной связи и параллельного соединения звеньев.
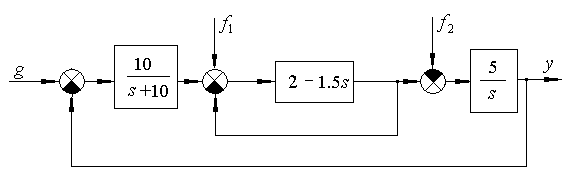
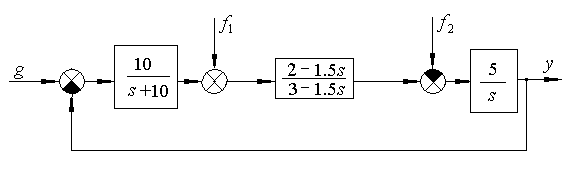
С учетом количества входных сигналов установившаяся ошибка в рассматриваемом примере определяется как сумма двух составляющих: 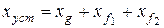 .
.
Найдем требуемые передаточные функции и рассчитаем установившуюся ошибку от задающего воздействия:
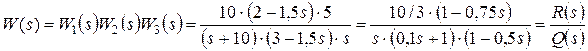 ,
,
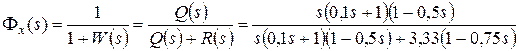 ,
,
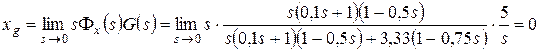 .
.
Выполним расчет для возмущения f1:
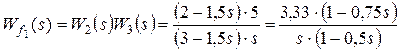 ,
,
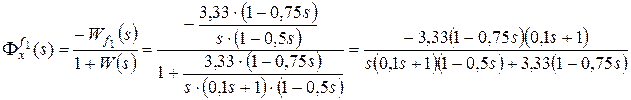 ,
,
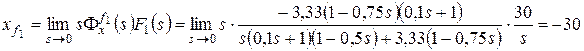 .
.
Выполним расчет для возмущения f2:
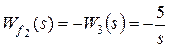 ,
,
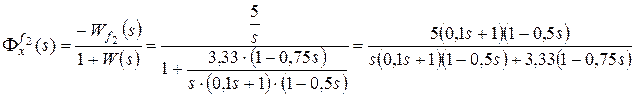 ,
,
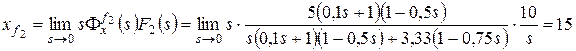 .
.
Результирующая установившаяся ошибка:
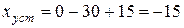 .
.








