Практическое занятие 2. Получение временных характеристик динамических звеньев
Переходная характеристика (переходная функция) – это реакция звена или системы на входной сигнал в виде единичной ступенчатой функции.
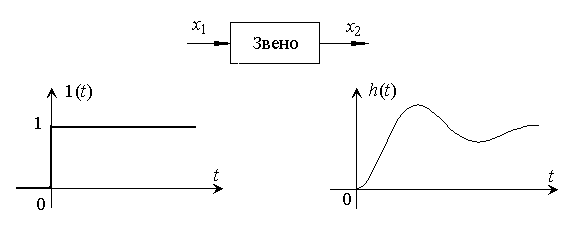
Рассмотрим наиболее удобные способы (методы) получения переходной характеристики.
Классический метод – путем решения дифференциального уравнения звена или системы.
Пример 1.
Найти переходную характеристику апериодического звена 1-го порядка.
Дифференциальное уравнение звена известно: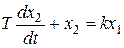 
.
В соответствии с определением переходной характеристики замене абстрактного входного сигнала x1 на единичную ступенчатую функцию будет соответствовать замена x2 на переходную характеристику (функцию):
.
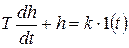Такая запись предусматривает решение дифференциального уравнения
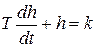
на интервале времени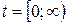 
.
Решение линейного неоднородного дифференциального уравнения ищут в виде суммы двух составляющих:
,
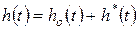где h0 – общее решение, h * – частное решение. В теории управления общее решение называют переходной составляющей, частное решение – вынужденной составляющей:
.
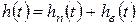Переходную составляющую находят как решение однородного дифференциального уравнения:
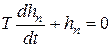
в форме суммы экспонент с произвольными коэффициентами. В показателях степени экспонент используются корни характеристического уравнения.
Например, если все корни вещественные, причем кратные корни отсутствуют, переходная составляющая имеет вид:
.
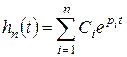В рассматриваемом примере характеристическое уравнение имеет вид:
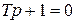
и имеет один корень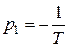 
.
В результате получим выражение для переходной составляющей:
.
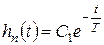Вынужденную составляющую находят в форме, соответствующей правой части. Если правая часть – константа, вынужденная составляющая – также константа, и для ее нахождения достаточно в уравнении положить производные равными нулю. В результате: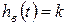 
.
Результирующее полное решение уравнения:
.
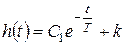Произвольные константы находят через начальные условия, которые для временных характеристик динамических звеньев принимаются равными нулю.
Найдем C1: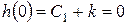 
, C1= - k .
В результате получена переходная характеристика:
.
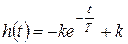Необходимо учесть, что в практических задачах переходные характеристики могут рассматриваться на различных временных интервалах. Для того, чтобы избавиться от необходимости отдельно указывать эту дополнительную информацию, выражения для переходных характеристик домножают на единичную ступенчатую функцию с соответствующим аргументом. Для рассматриваемого примера результат должен быть представлен в следующем виде:
.
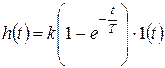График переходной характеристики показан на рисунке.
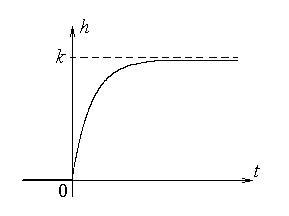
Полученная характеристика показывает, что апериодическое звено 1-го порядка воспроизводит входной сигнал. Но это происходит с замедлением – по окончании переходного процесса. То есть данное звено характеризуется инерционностью.
Отметим дополнительно, что при наличии производных в правой части уравнения может возникнуть необходимость учитывать скачкообразное изменение начальных условий. Поэтому с учетом наличия других методов классический можно рекомендовать для решения уравнений без производных в правой части.
На основе полученной характеристики полезно проанализировать влияние параметров звена на его динамические свойства.
На следующем рисунке показаны варианты переходной характеристики для двух различных значений постоянной времени.
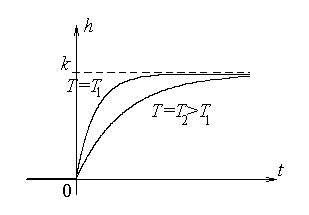
Таким образом, при увеличении значения постоянной времени переходный процесс замедляется. Постоянная времени характеризует инерционность динамического звена.
Теперь рассмотрим влияние на процесс в звене коэффициента передачи.
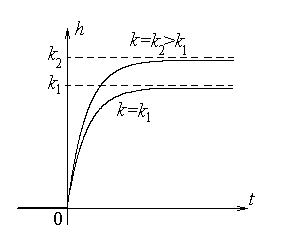
Операторный метод – на основе передаточной функции звена.
Воспользуемся определениями передаточной функции и переходной характеристики с учетом известного изображения по Лапласу единичной ступенчатой функции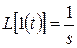 
:
.
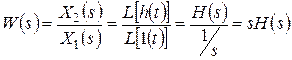Следовательно, при заданной передаточной функции изображение переходной характеристики можно найти по формуле:
.
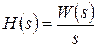После этого переходная характеристика может быть найдена путем перехода от изображения к оригиналу одним из следующих способов:
- непосредственно с помощью таблицы изображений – в простейших случаях;
- разложением H(s) на сумму табличных изображений;
- с помощью теорем разложения.
Пример 2.
Найти переходную характеристику дифференцирующего звена с замедлением.
Передаточная функция звена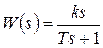 
.
Найдем изображение переходной характеристики:
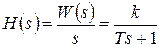
и воспользуемся следующей строкой из таблицы изображений.
| Оригинал | Изображение |
| 
|
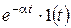
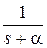
Преобразуем имеющееся изображение к табличному виду:
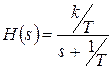
и с учетом линейности преобразования Лапласа получим искомую характеристику:
.
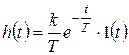График переходной характеристики показан на рисунке.
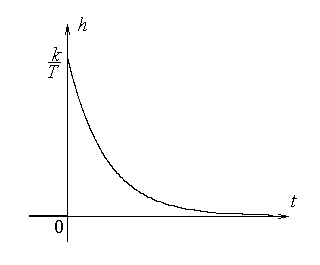
Пример 3.
Найти переходную характеристику интегрирующего звена с замедлением.
Передаточная функция звена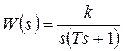 
.
Найдем изображение переходной характеристики:
.
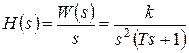Поскольку такое изображение в таблицах, как правило, отсутствует, разложим изображение на сумму:
.
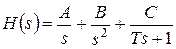Приведя разложение к общему знаменателю
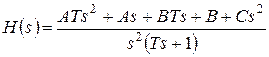
и приравняв числители полученного и исходного выражений, получим уравнения для коэффициентов:
AT+C=0,
A+BT=0,
B=k,
откуда A = - kT,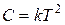 
.
Слагаемые в разложении соответствуют следующим строкам таблицы изображений.
| Оригинал | Изображение |
| 1(t) |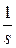 
|
| 
|
|
|
|
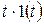
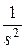
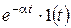
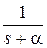
В результате получим:
.
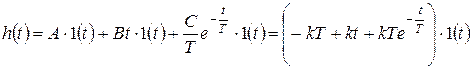Для построения характеристики сначала рассмотрим графики двух слагаемых полученного выражения, которые помогают получить итоговый график.
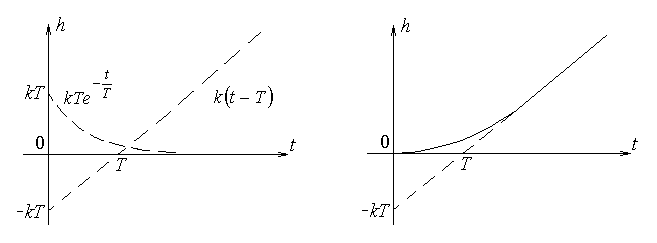
В наиболее сложных случаях для нахождения оригинала по изображению используют теоремы разложения.
Пример 4.
Найти переходную характеристику колебательного звена.
Передаточная функция звена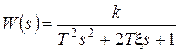 
, причем 
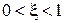и корни знаменателя комплексные.
Найдем изображение переходной характеристики:
.
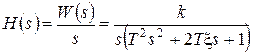Воспользуемся одной из теорем разложения:
для изображения вида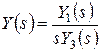 
оригинал имеет форму 
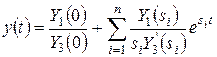, где si – корни полинома Y3.
Корни полинома Y3 в рассматриваемом примере имеют вид: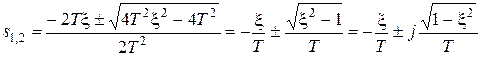 
.
Производная Y3: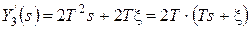 
Перейдем к оригиналу:
.
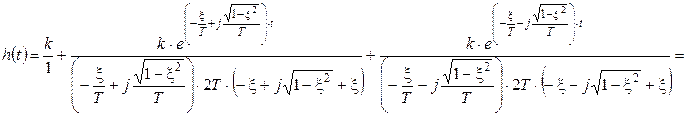
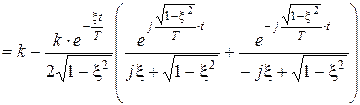Теперь учтем теорему Эйлера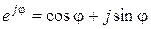 
и соответственно 
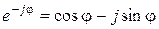, а также соотношения: 
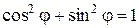и 
.
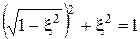Все это позволяет ввести в рассмотрение угол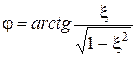 
, причем принять 
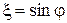и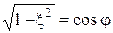 
. С учетом этих соотношений продолжим преобразование выражения для переходной характеристики:
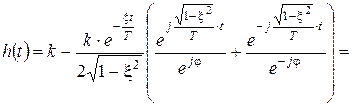
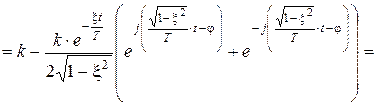
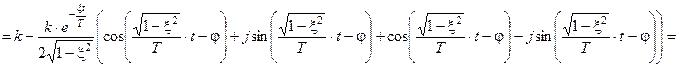
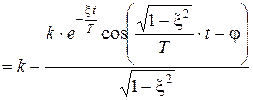
и окончательно
.
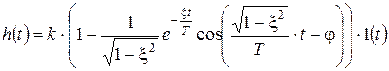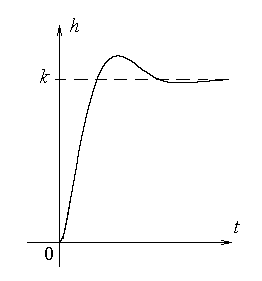
График характеристики отображает затухающий колебательный процесс.
Весовая характеристика (весовая функция, функция веса) – это реакция звена или системы на входной сигнал в виде d-функции (функции Дирака).
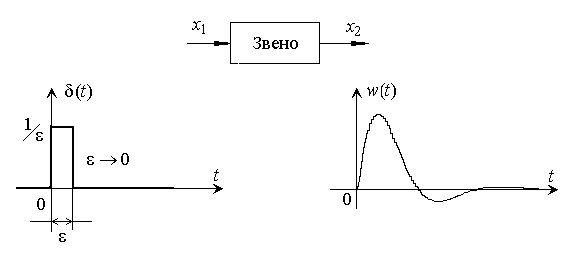
Вспомним основные свойства d-функции:
, 
, 
.
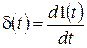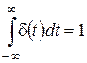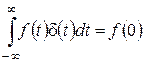Рассмотрим наиболее удобные способы (методы) получения весовой характеристики.
Операторный метод.
Воспользуемся определениями передаточной функции и весовой характеристики с учетом известного изображения по Лапласу d-функции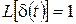 
:
.
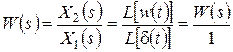Следовательно, передаточная функция является изображением по Лапласу функции веса.
Пример 5.
Найти весовую характеристику апериодического звена 1-го порядка.
Преобразуем передаточную функцию звена к табличному виду
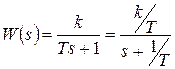
и запишем результат:
.
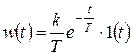График весовой характеристики показан на рисунке.
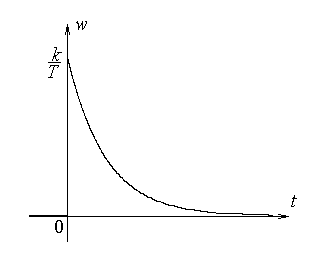
Получение весовой функции дифференцированием переходной характеристики.
Следствием полученного выше соотношения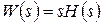 
является следующая связь между весовой и переходной функциями:
.
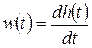Вернемся к последнему примеру.
Переходная характеристика апериодического звена 1-го порядка была получена выше:
.
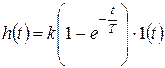Продифференцируем ее:
.
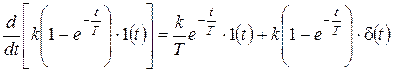С учетом тождественного равенства нулю d-функции при всех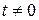 
упростим полученное выражение:
.
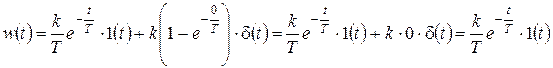Теперь проведем краткий анализ динамических свойств типовых звеньев, отражаемых переходной характеристикой.
На рисунке 46 показаны переходные характеристики типовых позиционных звеньев.
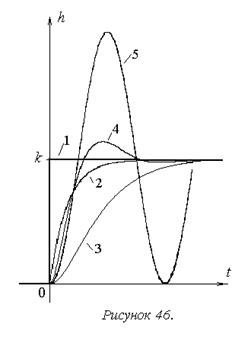
На основе их сравнительного анализа можно сделать следующие выводы:
1. Общим свойством звеньев данной группы является пропорциональность выходного сигнала входному, обеспечиваемая по окончании переходного процесса. Именно это свойство является единственным для идеального звена данной группы – безынерционного (1).
2. Общее отличие всех звеньев от безынерционного состоит в наличии переходного процесса, вызванном их инерционностью. Различия же между звеньями внутри группы определяются количеством и соотношением постоянных времени, то есть характером инерционности.
Так процесс в звеньях второго порядка – апериодическом 2-го порядка (3), колебательном (4) и консервативном(5) – в отличие от апериодического звена 1-го порядка (2), начинает развиваться не мгновенно, так как здесь и начальная скорость изменения сигнала – нулевая.
Кроме того, в зависимости от соотношения постоянных времени у звеньев второго порядка наблюдается различный характер процесса.
Динамические свойства, отражаемые переходной характеристикой, определили названия типовых динамических звеньев.
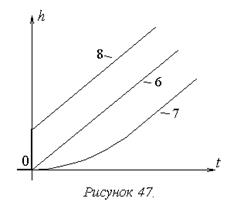
На рисунке 47 показаны переходные характеристики типовых интегрирующих звеньев.
На основе их сравнительного анализа можно сделать следующие выводы:
1. Общее свойство звеньев данной группы отражается характеристикой идеального интегрирующего звена (6) – в установившемся процессе выходной сигнал пропорционален интегралу входного.
2. У остальных звеньев данной группы проявляются дополнительные динамически свойства: инерционность у интегрирующего звена с замедлением (7) и противоположный эффект у изодромного звена (8), приводящий к тому, что процесс в данном звене ускоряется по сравнению с процессом в идеальном звене. Формально такая разница в динамических свойствах отражается расположением постоянной времени в передаточной функции: в знаменателе при наличии инерционности и в числителе в противоположном случае.
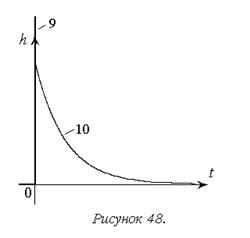
На рисунке 48 показаны переходные характеристики типовых дифференцирующих звеньев.
На основе их сравнительного анализа можно сделать следующие выводы:
1. Общее свойство звеньев данной группы отражается характеристикой идеального дифференцирующего звена (9) – в установившемся процессе выходной сигнал пропорционален производной входного.
2. Наличие инерционности у дифференцирующего звена с замедлением (10) приводит к переходному процессу.