Пересечение множеств
· Пересечением (произведением) множеств 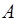 и
и 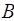 называется множество, обозначаемое
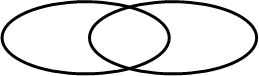
называется множество, обозначаемое 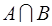 и состоящее из всех тех и только тех элементов, которые принадлежат и множеству
и состоящее из всех тех и только тех элементов, которые принадлежат и множеству 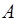 , и множеству
, и множеству 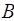 :
:
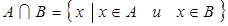
А 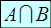 В
В
Объединение множеств
· Объединением (сумма) множеств 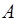 и
и 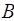 называется множество
называется множество 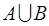 , состоящее только из тех элементов, которые принадлежат хотя бы одному из множеств
, состоящее только из тех элементов, которые принадлежат хотя бы одному из множеств 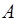 или
или 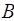 :
:
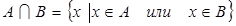 .
.



А 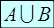 В
В
Объединение множеств 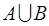 содержит все элементы множества
содержит все элементы множества 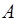 и все элементы множества
и все элементы множества 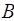 .
.
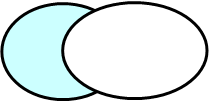
Вычитание множеств
· Разностью между множествами 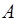 и
и 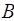 называется множество
называется множество 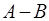 ( А \ В), состоящее из тех элементов множества
( А \ В), состоящее из тех элементов множества 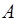 , которые не принадлежат множеству
, которые не принадлежат множеству 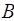 , то есть
, то есть 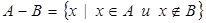 .
.
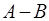
Дополнение множества
Часто множества 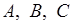 , … являются подмножествами некоторого более широкого множества
, … являются подмножествами некоторого более широкого множества 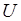 , принимаемого за универсальное.
, принимаемого за универсальное.
· Для совокупности множеств 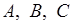 , ... универсальным множеством называют каждое множество
, ... универсальным множеством называют каждое множество 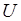 такое, что
такое, что 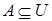 ,
, 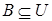 ,
, 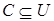 , ... .
, ... .
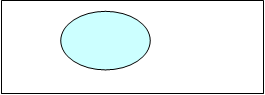
· Множество элементов универсального множества 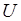 , не принадлежащих множеству
, не принадлежащих множеству 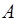 , называется дополнением множества
, называется дополнением множества 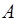 до множества
до множества 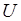 или просто дополнением и обозначается
или просто дополнением и обозначается 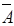 . Таким образом,
. Таким образом, 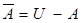 .
.
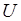
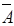
2. Комбинаторика занимается различного рода соединениями, которые можно образовать из элементов некоторого конечного множества. Термин "комбинаторика" происходит от латинского combina - сочетать, соединять.
Комбинаторикой называется раздел математики, изучающей вопрос о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Размещение с повторением. Из множества, содержащего m элементов, нужно выбрать k элементов, причем выбранный элемент, после того, как его взяли, вновь возвращается в исходное множество (то есть элементы в выбранном множестве могут повторяться).
Пользуясь правилом произведения, получим, что каждый из k элементов может быть выбран m способами. Таким образом, общее число комбинаций равно 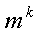 .
.
Пример 1. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5, 7.
Решение. Первой цифрой в числе может быть любая из четырех имеющихся. То же самое можно сказать и о последующих цифрах числа, поэтому общее число комбинаций: 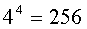
Размещениями без повторений из n элементов по m в комбинаторике называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Число размещений в комбинаторике обозначается Anm и вычисляется по формуле:
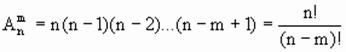
Пример 2. Сколько различных четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, при условии. Что цифры в числе не повторяются?
Решение. Общее число комбинаций равно числу размещений из 6 элементов по 4: 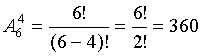
Перестановкой из m различных элементов называются комбинации, которые состоят из m элементов и отличаются друг от друга только порядком их расположения.
Число перестановок из m элементов равно: 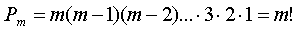
Пример 3. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5. 7, если цифры в числе не повторяются?
Решение. Количество чисел равно числу перестановок из четырех элементов: 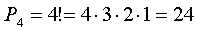
Сочетаниями из n элементов по m элементов (m  n) называются комбинации, состоящие из m элементов, взятых из данных n различных элементов, отличающиеся друг от друга только составом.
n) называются комбинации, состоящие из m элементов, взятых из данных n различных элементов, отличающиеся друг от друга только составом.
Число сочетаний из n элементов по m элементов вычисляется по формуле: 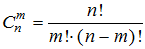
Пример 4. В группе 10 студентов. Сколькими способами можно выбрать из этой группы троих студентов для участия в конференции?
Решение. Число способов равно числу сочетаний из 10 элементов по 3 элемента: 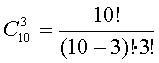 .
.
Методические указания к выполнению заданий:
Указания для задания №1:
Задача. Даны множества на числовой прямой A= 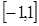 ; B=
; B= 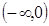 ; C=
; C= 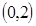 .
.
Найти следующие множества: А 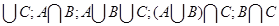 и изобразить их на числовой оси.
и изобразить их на числовой оси.
Решение.
-Множество A 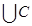 состоит из точек числовой прямой ,которые принадлежат либо множеству A ,либо множеству C:
состоит из точек числовой прямой ,которые принадлежат либо множеству A ,либо множеству C:
A 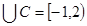 .
.
-Множество A 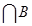 состоит из точек числовой прямой, которые принадлежат одновременно и множеству A и множеству B.
состоит из точек числовой прямой, которые принадлежат одновременно и множеству A и множеству B.
A 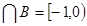 .
.
-Множество A 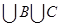 состоит из точек числовой прямой, которые принадлежат хотя бы одному из множеств A, B или C.
состоит из точек числовой прямой, которые принадлежат хотя бы одному из множеств A, B или C.
A 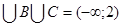 .
.
-Множество ( A 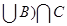 состоит из точек числовой прямой, которые принадлежат одновременно множеству A
состоит из точек числовой прямой, которые принадлежат одновременно множеству A 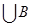 и множеству C. Построим множество A
и множеству C. Построим множество A 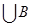 :
:
A 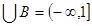
-Построим здесь же множество ( A 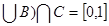
-Множество B 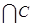 состоит из точек числовой прямой, которые принадлежат одновременно и множеству B и множеству C.
состоит из точек числовой прямой, которые принадлежат одновременно и множеству B и множеству C.
-B 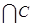 = Ø так как у этих множеств нет общих точек.
= Ø так как у этих множеств нет общих точек.
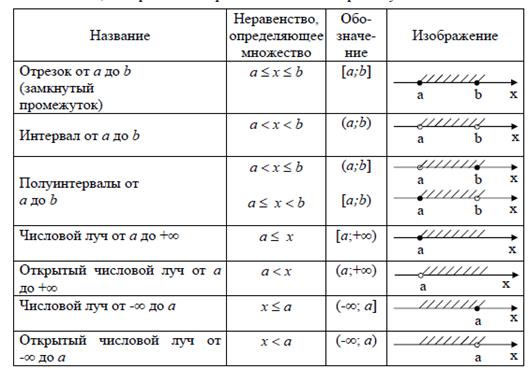
Таблица . Правила изображения числовых промежутков.
Указания для заданий № 5 - 7:
1. При выполнении заданий следует применять формулы для перестановок, размещений и сочетаний элементов.
2. Следует помнить, что внутри размещения элементы отличаются друг от друга.
3. В комбинаторных задачах результаты должны быть положительными и целыми.
 ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ СТУДЕНТАМИ:
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ СТУДЕНТАМИ:
| Вариант - 1 | Вариант - 2 |
1. Даны множества на числовой прямой А,В и С. Найти множества:
А 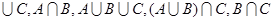 и изобразить их на числовой оси.
А= и изобразить их на числовой оси.
А= 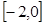 , В= , В= 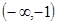 , С= , С= 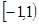
| 1. Даны множества на числовой прямой А,В и С. Найти множества:
А 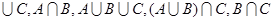 и изобразить их на числовой оси.
А= и изобразить их на числовой оси.
А= 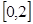 , В= , В= 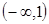  , С= , С= 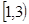
|
| 2. Сравнить множество А с множествами B, C, D. а) Если множества пересекаются, найти их пересечения. б) Найти универсальное множество для данных множеств. в) Изобразить отношения между множествами с помощью кругов Эйлера - Венна. А = {красный, желтый, синий, зеленый}. B = {красный, желтый}. С = {желтый, синий, черный, оранжевый}. D = {коричневый, голубой, розовый}. | 2. Сравнить множество А с множествами B, C, D. Сравнить множества B, C, D. а)Найти попарно пересечение множеств В, С, D. б) Найти универсальное множество для данных множеств. в) Изобразить отношения между множествами с помощью кругов Эйлера-Венна. А = {а | a – студент ВГСПУ}. B = {b | b – студент - филолог ВГСПУ }. С = {с | с– студент-историк ВГСПУ }. D = {d | d – студент первого курса ВГСПУ}. |
| 3. Сколько человек в группе занимается спортом, если 9 человек занимаются лыжами и плаванием, а 12 человек – плаванием и волейболом, причем в секцию по плаванию ходят 4 человека из групп? | 3.Пятьдесят лучших студентов колледжа наградили за успехи поездкой в англию и Германию. Из них 5 - не владели ни одним разговорным иностранным языком, 34 – знали английский язык и 27 – немецкий. Сколько студентов владели двумя разговорными иностранными языками ? |
| 4. Найти множество, являющееся пересечением множеств А={д, е, ф, ж, в, г, п, с} и В={а, б, г, и, к, л. ж о} и мощность найденного множества. Построить диаграммы Эйлера-Венна. | 4. Найти множество, являющееся объединением множеств А={h, l, m, p, q} и В={l, p, o, g, t, s, h} и мощность найденного множества. Найти универсальное множество для множеств А и В. Построить диаграммы Эйлера-Венна. |
| 5. Найдите значения выражения: | |
а) 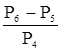 б)
б) 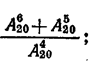 в)
в) 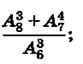 г)
г) 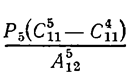
| а) 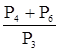 б)
б) 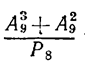 в)
в) 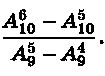 г)
г) 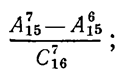
|
| 6. Сколькими способами можно выбрать 3-х дежурных, если в классе 30 человек? | 6. Научное общество состоит из 25 человек. Надо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами может быть сделан этот выбор, если каждый член общества может занимать лишь один пост? |
| 7.На 7 сотрудников выделены 5 различных путевок. Сколькими способами их можно распределить среди сотрудников? | 7. Сколькими способами можно переставить буквы в слове «ДЕЛЕНИЕ»? |
| Вариант - 3 | Вариант -4 |
1. Даны множества на числовой прямой А,В и С Найти множества
А 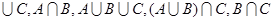 и изобразить их на числовой оси.
А= и изобразить их на числовой оси.
А= 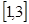 , В= , В= 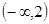 , С= , С= 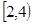
| 1. Даны множества на числовой прямой А,В и С Найти множества
А 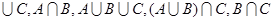 и изобразить их на числовой оси.
А= и изобразить их на числовой оси.
А= 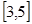 , В= , В= 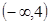 , С= , С= 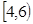
|
| 2. Найти множество, являющееся объединением множеств А= {1, 2, 5, 7, 10}и В = {2, 3, 5, 6, 7, 9}, и мощность найденного множества. Найти универсальное множество для множеств А и В. Построить диаграммы Эйлера-Венна. | 2. Найти множество, являющееся разностью множеств А= {1, 2, 5, 7, 10}и В = {2, 3, 5, 6, 7, 9}, и мощность найденного множества. Построить диаграммы Эйлера-Венна. |
| 3.Каждый студент группы программистов занимается в свободное время либо в НСО, либо спортом. Сколько студентов в группе, если 23 – увлекаются спортом, 12 – занимаются в НСО, а 7 – совмещают занятия в НСО и увлечение спортом ? | 3. В классе 35 учащихся. Из них 20 посещают математический кружок, 11 – физический, 10 учащихся не посещают ни одного их этих кружков. Сколько учеников посещают и математический, и физический кружок ? |
| 4. Найти множество, являющееся разностью множеств А={a, b, c, d, e, f, g} и В={h, i, j, a, k, l, f} и мощность найденного множества. Найти универсальное множество для множеств Аи В. Построить диаграммы Эйлера-Венна. | 4. Даны множества А={2, 3, 5, 8, 13, 15}, В={1, 3, 4, 8,16}, С={12, 13, 15, 16}, D={0, 1, 20}. Найти множества, являющееся А ∩ В ∩ С, D\В, и мощность каждого из найденных множеств. Построить диаграммы Эйлера – Венна. |
| 5. Найдите значения выражения: | |
а) 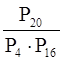 б)
б) 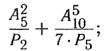 в)
в) 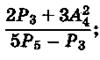 г)
г) 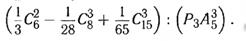
| а) 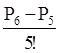 б)
б) 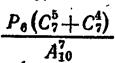 в)
в) 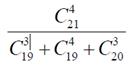 г)
г) 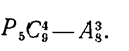
|
| 6. Сколькими способами собрание, состоящее из 18 человек, может выбрать из своего состава председателя собрания и секретаряз его выбрать ловек ажков книг333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333? | 6. Тренер отбирает 5 спортсменов из 12. Сколькими способами он может составить команду? |
| 7.Сколько перестановок можно сделать из букв слова « МИССИСИПИ» ? | 7.Сколько вариантов распределения 3- х путевок в санаторий различного профиля можно составить для 5 претендентов? |
Выполненную и правильно оформленную работу предоставить преподавателю.








