Тема: «Операции над множествами. Решение комбинаторных задач.»
Практическое занятие № 5
Тема: «Операции над множествами. Решение комбинаторных задач.»
Цель: 1.Сформировать навыки решения заданий, связанных с базовыми понятиями теории множеств и операций над множествами, типовых комбинаторных задач.
2. Способствовать развитию логического мышления, памяти, внимания.
3. Способствовать привитию сознательного приобретения новых знаний по теме.
Теоретические сведения к практической работе:
1. Множество относится к математическим объектам, для которых нет строгого определения. Другим примером неопределяемого понятия служит точка в геометрии.
Один из основателей теории множеств Г. Кантор определял множество так: "Множество есть многое, мыслимое как целое".
Множество - это совокупность объектов, называемых элементами множества. Объекты, которые образуют множество, называются элементами этого множества. Пример: Множество S = {3, 2, 11, 5, 7} - элементы множества записывают в фигурных скобках.
Некоторые множества имеют стандартные названия и обозначения:
Æ — пустое множество;
N = {1, 2, 3, ...} — множество натуральных чисел;
Z = {0, ±1, ±2, ±3, ...} — множество целых чисел;
Q = {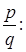 
p, qÎ Z, q¹0} — множество рациональных чисел;
R = {все десятичные дроби} — множество вещественных чисел.
Множества, состоящие из одних и тех же элементов, называются равными (одинаковыми). Пишут А=В.
Множество, которое не содержит ни одного элемента, называется пустым и обозначается символом ∅. Принято считать, что пустое множество является подмножеством любого множества, ÆÍ А, где А – любое множество. Таким образом, всякое множество содержит в качестве своих подмножеств пустое множество и само себя.
Если каждый элемент множества А является элементом множества В, говорят, что множество А является подмножеством множества В, и записывают А ÍВ или В Ê А. Отметим, что по определению само множество А является своим подмножеством, т.е. А ÍА.
Если АÍВ и В ÍА, то по ранее введенному определению А = В.
Если АÍВ и А ¹В, то А есть собственное подмножество В, А ÌВ. Если А не является собственным подмножеством В, то записывают А ËВ.
Множества могут быть конечными или бесконечными. Конечное множество состоит из конечного числа элементов, например, множество страниц в книге, множество студентов в группе и т.д.
Бесконечное множество состоит из бесконечного числа элементов, т.е. это множество, которое не является ни конечным, ни пустым. Например: множество действительных чисел, множество точек плоскости, множество атомов во Вселенной и т.д.
Мощностью конечного множества называется количество его элементов. Мощность множества A обозначается m (A) или |А|.
Множество всех подмножеств данного множества А называется множеством-степенью и обозначается P(A). Множество P(A) состоит из 2nэлементов.